НОУ ИНТУИТ | Введение в математическое моделирование. Лекция 11: Компьютерное моделирование при обработке опытных данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 15.03.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Донецкий национальный технический университет

|

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать программу

Сглаживание опытных данных методом наименьших квадратов

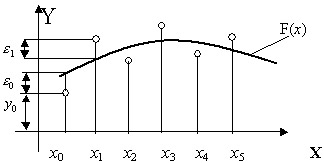
В этом методе при сглаживании опытных данных аппроксимирующей кривую F(x) стремятся провести так, чтобы ее отклонения 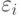$\varepsilon_i$ от табличных данных (уклонения) по всем узловым точкам были минимальными (рис 11.6), т.е.

$\varepsilon_i=\left|F(x_i) - y_i \right| \to min.$

( 11.6)

Рис. 11.6.

Избавимся от знака уклонения. Тогда условие (11.6) будет иметь вид:

$\varepsilon_i^2=\left|(F(x_i) - y_i)^2 \right| \to min.$

( 11.7)

Суть метода наименьших квадратов заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость F(x), сумма квадратов уклонений которой от табличных данных по всем узловым точкам была бы минимальной, т.е.

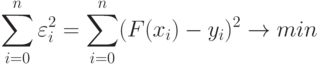$\sum \limits_{i=0}^{n}\varepsilon_i^2 = \sum \limits_{i=0}^{n} (F(x_i) - y_i)^2 \to min$

( 11.8)

Для определенности задачи искомую функцию F(x) будем выбирать из класса алгебраических многочленов степени m:

$P_m(x) = a_0 x^m + a_1 x^{m-1} + a_2 x^{m-2} + \ldots + a_{m-1} x^1 + a_m.$

( 11.9)

Назовем многочлен (11.9) аппроксимирующим многочленом. Аппроксимирующий многочлен не проходит через все узловые точки таблицы. Поэтому его степень m не зависит от числа узловых точек. При этом всегда m < n. Степень m может меняться в пределах $1 \le m \le N-2$ .

Если m=1, то мы аппроксимируем табличную функцию прямой линией. Такая задача называется линейной регрессией.

Если m=2, то мы аппроксимируем табличную функцию квадратичной параболой. Такая задача называется квадратичной аппроксимацией.

Если m=3, то мы аппроксимируем табличную функцию кубической параболой. Такая задача называется кубической аппроксимацией.

Уточним метод наименьших квадратов: для табличной функции, полученной в результате эксперимента, построить аппроксимирующий многочлен (11.9) степени m, для которого сумма квадратов уклонений по всем узловым точкам минимальна, т.е.

$S = \sum \limits_{0}^{n} (P_m(x_i) - y_i) \to min.$

( 11.10)

Изменим вид многочлена P_m. Поставим на последнее место слагаемые, содержащие x^m. На предпоследнее - слагаемые, содержащие x^m-1 и т.д. В результате получим:

$P_m(x) = a_0 x^0+ a_1 x^1 + a_2 x^2 + \ldots + a_m x^m.$