НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 6: Численное решение нелинейных алгебраических уравнений и систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать программу

Тогда счет в банке изменился бы по закону

$u_{k + 1} = \left[{1 + \delta_0 \left({1 - \frac{u_k}{u_{\max }}}\right)}\right]u_k ,$

( 5.7)

т.е. в соответствии с моделью (5.6).

Так как $u_k \in [0, 1],$ то $\lambda \in [0, 4].$ Отображение (5.6) называется логистическим. К нему можно также придти, применив простейший из численных методов решения обыкновенных дифференциальных уравнений — явный метод Эйлера ( "Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений" ) для решения дифференциального уравнения динамики популяции (уравнения Ферхюльста)

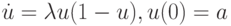$\dot {u} = \lambda u(1 - u), u(0) = a$

( 5.8)

где u — численность популяции. Вводя шаг по времени, получим разностный аналог уравнения (5.8):

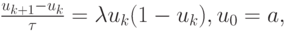${\frac{u_{k + 1} - u_k}{\tau } = \lambda u_k (1 - u_k), u_0 = a},$

( 5.9)

откуда получаем

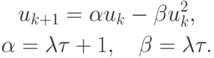$\begin{gather*} u_{k + 1} = \alpha u_k - \beta u_k^2, \\ \alpha = \lambda \tau + 1, \quad \beta = \lambda \tau . \end{gather*}$

( 5.10)

И отображение (5.7), и отображение (5.10) легко приводится к виду (5.6). Достаточно произвести очевидную замену переменных. Для (5.10) эта замена будет

$$ \mu = \alpha , z_k = \frac{\alpha }{\beta }u_k $.$

Как двумерное обобщение логистического отображения можно рассматривать отображение Хенона

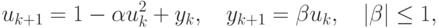${u_{k + 1} = 1 - \alpha u_k^2 + y_k , \quad y_{k + 1} = \beta u_k, \quad \left|\beta\right| \le 1, }$

( 5.11)

или

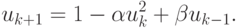$u_{k + 1} = 1 - \alpha u_k^2 + \beta u_{k - 1}.$

( 5.12)

К довольно известным двумерным дискретным моделям относится также отображение Чирикова, предложенное для моделирования поведения незатухающего ротатора, возбуждаемого внешними толчками:

$u_{k + 1} = u_k - \alpha \sin y_k , y_{k + 1} = y_k + u_{k + 1}.$

( 5.13)

Рассмотрим подробнее свойства отображения:

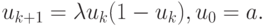
$u_{k + 1} = \lambda u_{k}(1 - u_{k}), u_{0} = a.$

Заметим, что f(0) = f(1) = 0 и 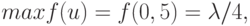$max f(u) = f(0, 5) = \lambda / 4,$ то при 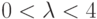$0 < \lambda < 4$ интервал X = [0, 1] отображается в себя,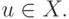 $u \in X.$

Введем обозначения

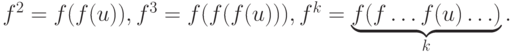
$f^2 = f(f(u)), f^3 = f(f(f(u))), f^{k} = \underbrace{f(f \ldots f(u) \ldots )}_k.$

Последовательность f, f₂, ..., f_k, ... называется траекторией отображения и обозначается 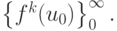$\left\{f^{k}(u_0) \right\}_0^\infty.$

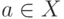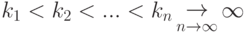Определение. Точка $a \in X$ ( X — множество, включающее в себя все значения отображения (5.4)) называется предельной точкой траектории $\left\{f^{k} (u_0 ) \right\}_{k = 0}^\infty,$ если существует последовательность $k_1 < k_2 < ... < k_n \mathop \to\limits_{n \to \infty } \infty$ такая, что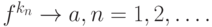 $f^{k_n} \to a, n = 1, 2, \ldots.$

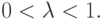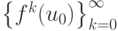Рассмотрим вначале случай $0 < \lambda < 1.$ На X = [0, 1] существует только одна предельная (или неподвижная) точка x = 0. Любая последовательность, $\left\{f^{k} (u_0 ) \right \}_{k = 0}^\infty$ сходится к предельной точке рассматриваемого отображения x = 0. Если рассматривается популяционная модель, то это означает, что рассматриваемая популяция не может выжить.

Из теоремы о сжимающем отображении следует, что последовательность 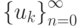$\left\{{u_k}\right\}_{n = 0}^\infty$ сходится к своей предельной точке, если $\left|{f^{\prime}_u}\right| \le 1.$