НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 3: Численное решение систем линейных алгебраических уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

2.4.2. Модификация метода Гаусса для случая линейных систем с трехдиагональными матрицами — метод прогонки

В приложениях часто возникают системы линейных уравнений с матрицами специального вида. В дальнейшем, например, при интерполяции функции сплайнами, при решении задачи Штурма-Лиувилля, при численном решении уравнений теплопроводности, уравнений Лапласа и Пуассона придется иметь дело с системами, матрицы которых имеют ненулевые элементы лишь на главной диагонали и еще на двух диагоналях — одной под главной, одной над главной. Такие матрицы называются трехдиагональными. Для решения систем с трехдиагональными матрицами существует экономичный (требующий малого количества памяти и арифметических действий) вариант метода Гаусса — прогонка. В англоязычной литературе метод прогонки называется алгоритмом Томаса. Подробнее о свойствах метода прогонки речь пойдет в "Численное решение краевых задач для систем обыкновенных дифференциальных уравнений" в связи с решением разностными методами задачи Штурма-Лиувилля.

2.4.3. LU-разложение

Среди прямых методов численного решения СЛАУ широко используется также LU-разложение матрицы $\mathbf{A}$ и метод Холецкого (или метод квадратного корня).

Если матрица $\mathbf{A}$ представима в виде произведений матриц $\mathbf{LU}$ , то СЛАУ может быть представлена в виде

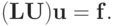$(\mathbf{LU})\mathbf{u} = \mathbf{f}.$

( 2.13)

Перепишем (2.13), вводя вспомогательный вектор $\mathbf{v}$ , в следующем виде

$\mathbf{Lv} = \mathbf{f},\quad \mathbf{Uu} = \mathbf{v}.$

( 2.14)

Решение СЛАУ свелось к последовательному решению двух систем с треугольными матрицами. Первый этап решения системы 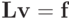$\mathbf{Lv} = \mathbf{f}$ :

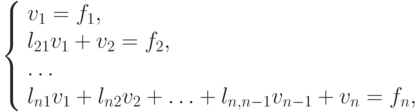
$\left\{ \begin{array}{l} v_1 = f_1 , \\ l_{21}v_1 + v_2 = f_2 , \\ \ldots \\ l_{n1}v_1 + l_{n2}v_2 + \ldots + l_{n,n - 1}v_{n - 1}+ v_n = f_n , \\ \end{array} \right.$

откуда можно вычислить все v_k последовательно по формулам

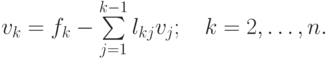
$v_k = f_k - \sum\limits_{j = 1}^{k - 1}{l_{kj}v_j};\quad k = 2, \ldots , n.$

Далее рассмотрим систему 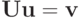$\mathbf{Uu} = \mathbf{v}$ или

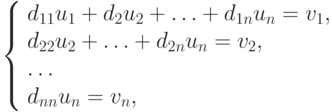
$\left\{ \begin{array}{l} d_{11}u_1 + d_2 u_2 + \ldots + d_{1n} u_n = v_1 , \\ d_{22}u_2 + \ldots + d_{2n} u_n = v_2 , \\ \ldots \\ d_{nn}u_n = v_n , \\ \end{array} \right.$

решение которой находится в обратном порядке, т.е. при k = n - 1, ..., 1 по очевидным формулам 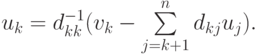$u_k = d_{kk}^{- 1}(v_k - \sum\limits_{j = k + 1}^n{d_{kj}u_j )}.$ Условия существования такого разложения даются следующей теоремой [2.5] (без доказательства).

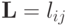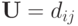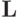Теорема. Если все главные миноры квадратной матрицы $\mathbf{A}$ отличны от нуля, то существуют единственные нижняя и верхняя треугольные матрицы $\mathbf{L} = l_{ij}$ и $\mathbf{U} = d_{ij}$ такие, что $\mathbf{A}= \mathbf{LU}.$ При этом все диагональные коэффициенты матрицы $\mathbf{L}$ фиксированы и равны единице.

Опишем алгоритм нахождения элементов l_ijd_ij матриц 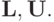$\mathbf{L}, \mathbf{U}.$ Выписав равенство $\mathbf{A} = \mathbf{LU}$ в компонентах, получим

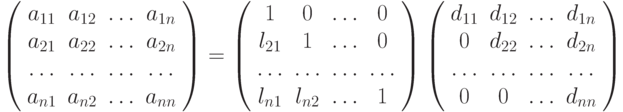
$\left( \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \\ \end{array} \right) = \left( \begin{array}{cccc} 1 & 0 & \ldots & 0 \\ l_{21} & 1 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ l_{n1} & l_{n2} & \ldots & 1 \\ \end{array} \right) \left( \begin{array}{cccc} d_{11} & d_{12} & \ldots & d_{1n} \\ 0 & d_{22} & \ldots & d_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & d_{nn} \\ \end{array} \right)$

Выполнив умножение матриц, приходим к системе линейных уравнений размером n x n:

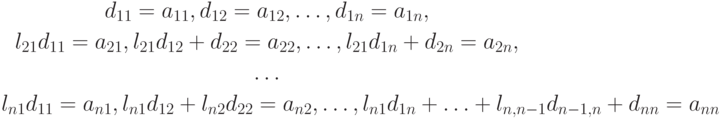
$\begin{gather*} d_{11} = a_{11}, d_{12}= a_{12}, \ldots , d_{1n} = a_{1n}, \\ l_{21}d_{11} = a_{21}, l_{21}d_{12}+ d_{22} = a_{22}, \ldots , l_{21}d_{1n}+ d_{2n} = a_{2n}, \\ \ldots \\ l_{n1}d_{11} = a_{n1}, l_{n1}d_{12} + l_{n2}d_{22} = a_{n2}, \ldots , l_{n1}d_{1n} + \ldots + l_{n,n-1}d_{n-1,n} + d_{nn} = a_{nn} \end{gather*}$

относительно неизвестных d₁₁, d₁₂, ..., d_1n, l₂₁, d₂₂, ..., d_2n, l_n1, l_n2, ..., d_nn.

Специфика этой системы позволяет решить ее последовательно. Из первой строки находим d_1j= a_1j(j = 1, ..., n).

Из уравнений, входящих в первый столбец приведенной выше системы, находим l_i1= a_i1/d₁₁, i = 1, ...dots, n. Теперь можно из уравнений второй строки найти d_2j= a_2j- l₂₁d_1j, j = 2, ..., n, а из уравнений, входящих во второй столбец, получим 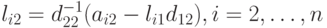$l_{i2}= d_{22}^{-1}(a_{i2}- l_{i1}d_{12}), i = 2, \ldots, n$ и так далее. Последним вычисляется элемент

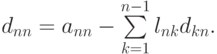
$d_{nn} = a_{nn}- \sum\limits_{k = 1}^{n - 1}{l_{nk}d_{kn}}.$

Можно выписать общий вид этих формул:

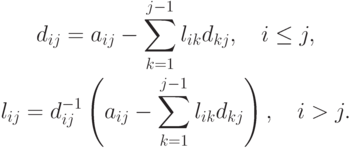
$\begin{gather*} d_{ij}= a_{ij} - \sum\limits_{k = 1}^{j - 1}{l_{ik}d_{kj}},\quad i \le j, \\ l_{ij}= d_{ij}^{- 1}\left({a_{ij} - \sum\limits_{k = 1}^{j - 1}{l_{ik}d_{kj}}}\right),\quad i > j. \end{gather*}$

Приведение матриц к треугольному виду аналогично приведению матрицы в методе Гаусса и также требует количества арифметических действий порядка O(n³), точнее, 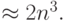$\approx 2n^{3}.$

2.4.4. Метод Холецкого (метод квадратного корня)

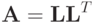Пусть матрица рассматриваемой линейной системы $\mathbf{A}$ — симметричная, т.е. a_ij = a_ji, положительная матрица. Тогда она представима в виде $\mathbf{A} = \mathbf{LL}^T$ , где

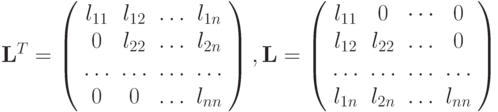
${\mathbf{L}}^T = \left( \begin{array}{cccc} l_{11} & l_{12} & \ldots & l_{1n} \\ 0 & l_{22} & \ldots & l_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & l_{nn} \end{array} \right), \mathbf{L} = \left( \begin{array}{cccc} l_{11} & 0 & \cdots & 0 \\ l_{12} & l_{22} & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ l_{1n} & l_{2n} & \ldots & l_{nn} \end{array} \right)$

Далее, как и в случае LU-разложения, решение СЛАУ 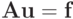$\mathbf{Au} = \mathbf{f}$ сводится к последовательному решению двух линейных систем с треугольными матрицами 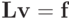$\mathbf{Lv} = \mathbf{f}$ , ${\mathbf{L}}^T{\mathbf{u}} = \mathbf{v}$ , для решения которых требуется примерно 2n² арифметических действий.

Первая из этих линейных систем

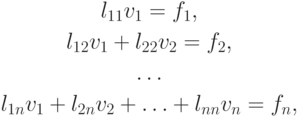
$\begin{gather*} l_{11}v_1 = f_1 ,\\ l_{12}v_1 + l_{22}v_2 = f_2 ,\\ \ldots\\ l_{1n}v_1 + l_{2n}v_2 + \ldots + l_{nn}v_n = f_n , \end{gather*}$

она легко решается. Для решения получаем очевидные формулы

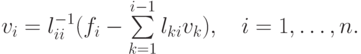
$v_i = l_{ii}^{- 1}(f_i - \sum\limits_{k = 1}^{i-1}{l_{ki}}v_k )},\quad i = 1,\ldots, n.$

Вторая система уравнений есть

l₁₁u₁  + l₁₂u₂  +  ...  + l_1nu_n  = v₁ , l₂₂u₂  +  ...  + l_2nu_n  = v₂, ... l_nnu_n  = v_n.

Из нее находим значения переменных u_i в обратном порядке по формуле

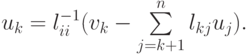
$u_k= l_{ii}^{- 1}(v_k - \sum\limits_{j = k + 1}^n{l_{kj}u_j)}.$

Определенной опасностью при реализации этого метода являются возможная близость к нулю l_ii и отрицательность подкоренных выражений при вычислении l_ii (последнего не должно быть при симметричной положительной матрице $\mathbf{A}$ )

Элементы матрицы 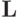$\mathbf{L}$ находим из уравнения 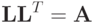${\mathbf{LL}}^T = \mathbf{A}$ , приравнивая соответствующие элементы матриц ${\mathbf{LL}}^T$ и $\mathbf{A}.$ В результате получим систему уравнений

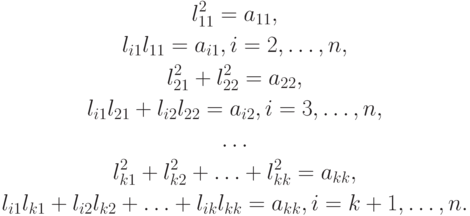
$\begin{gather*} l_{11}^2 = a_{11}, \\ l_{i1}l_{11} = a_{i1}, i = 2, \ldots ,n, \\ l_{21}^2 + l_{22}^2 = a_{22}, \\ l_{i1}l_{21} + l_{i2}l_{22} = a_{i2}, i = 3, \ldots , n, \\ \ldots\\ l_{k1}^2 + l_{k2}^2 + \ldots + l_{kk}^2 = a_{kk}, \\ l_{i1}l_{k1} + l_{i2}l_{k2} + \ldots + l_{ik}l_{kk} = a_{kk}, i = k + 1, \ldots , n. \end{gather*}$

Решение этой системы легко находится:

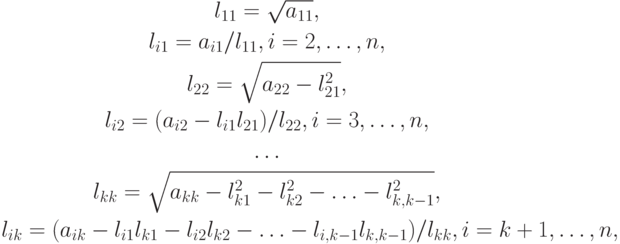
$\begin{gather*} l_{11} = \sqrt{a_{11}},\\ l_{i1} = a_{i1}/l_{11}, i = 2, \ldots , n, \\ l_{22} = \sqrt{a_{22}- l_{21}^2}, \\ l_{i2} = (a_{i2}- l_{i1}l_{21})/l_{22}, i = 3, \ldots ,n, \\ \ldots \\ l_{kk} = \sqrt{a_{kk}- l_{k1}^2 - l_{k2}^2 - \ldots - l_{k,k - 1}^2}, \\ l_{ik} = (a_{ik}- l_{i1}l_{k1}- l_{i2}l_{k2}- \ldots - l_{i,k - 1}l_{k,k - 1})/l_{kk},i = k + 1, \ldots , n, \end{gather*}$

Метод также называется методом квадратного корня.

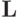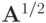Внимание! Не следует путать матрицу (оператор) $\mathbf{L}$ с оператором $\mathbf{A}^{1/2}$ — квадратным корнем из самосопряженного положительного оператора.

Дальше >>

Введение в вычислительную математику

Введение в вычислительную математику

Численное решение систем линейных алгебраических уравнений

2.4.2. Модификация метода Гаусса для случая линейных систем с трехдиагональными матрицами — метод прогонки

2.4.3. LU-разложение

2.4.4. Метод Холецкого (метод квадратного корня)

Вопросы и ответы

Студенты

Авторизоваться

Введение в вычислительную математику

Введение в вычислительную математику

Численное решение систем линейных алгебраических уравнений

2.4.2. Модификация метода Гаусса для случая линейных систем с трехдиагональными матрицами — метод прогонки

2.4.3. LU-разложение

2.4.4. Метод Холецкого (метод квадратного корня)

Вопросы и ответы

Студенты