НОУ ИНТУИТ | Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования. Лекция 2: Финансово-экономические модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 27.05.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Уральский государственный экономический университет

|

Вам нравится? Нравится 25 студентам

| Поделиться |

Поддержать программу

2.3. Финансовая рента

Рассмотрим последовательность распределенных во времени выплат и платежей [8,9]. Поток платежей, все составляющие которого положительны и поступают через одинаковые интервалы времени, называется финансовой рентой или аннуитетом. Пусть имеем постоянную финансовую ренту (рента называется постоянной, если все платежи имеют одинаковую величину), периодический платеж pmt=const .

Будущая стоимость ренты

Рассмотрим будущую стоимость ренты 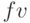за лет, для простоты пусть проценты начисляются один раз в год. Наращение стоимости ренты осуществляется за счет поступающих платежей и начисления на них процентов, причем, срок наращения каждого нового платежа на единицу меньше предыдущего. Будущая стоимость ренты имеет вид:

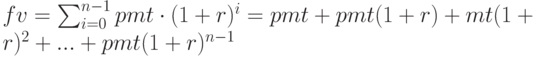$fv=\sum_{i=0}^{n-1}pmt\cdot (1+r)^i=pmt+pmt(1+r)+mt(1+r)^2+...+pmt(1+r)^{n-1}$

( 2.15)

Ряд (2.15) представляют собой геометрическую прогрессию. Для членов геометрической прогрессии $a_0, a_1 , a_2 ,...,a_{n-1}$ со знаменателем $\frac{a_k}{a_{k-1}}=q$ сумма равна

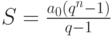$S=\frac{a_0(q^n-1)}{q-1}$

( 2.16)

Будущая стоимость ренты (2.15) - геометрическая прогрессия с 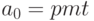a_0 = pmt , q=1+r . Тогда

( 2.17)

Размер платежа при наращении ренты можно определить из (2.17)

$pmt=\frac{fv\cdot r}{(1+r)^n-1}$

( 2.18)

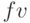Срок накопления будущей суммы при заданных процентной ставке и платеже pmt из (2.18) может быть определен следующим образом.

$\frac{fv}{pmt}\cdot r+1=(1+r)^n$ или

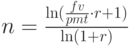$n=\frac{\ln(\frac{fv}{pmt}\cdot r +1)}{\ln(1+r)}$

( 2.19)

Современная стоимость ренты

Деньги, полученные в настоящий момент, более предпочтительны, чем деньги, которые будут получены в будущем. Для потока платежей представляет интерес оценка стоимости на начальный момент времени – современная стоимость. Переоценка будущего платежа на более ранний момент времени, называется математическим дисконтированием. Процентная ставка , с учетом которой оценивается современная стоимость, называется ставкой дисконтирования. Дисконтирование денежного платежа pmt на -м шаге осуществляется путем умножения его значения на коэффициент дисконтирования $\frac{1}{(1+r)^m}$ , тогда дисконтированная стоимость 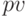потока платежей ренты к начальному моменту по ставке равна:

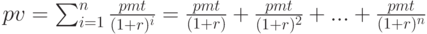$pv=\sum_{i=1}^{n}\frac{pmt}{(1+r)^i}=\frac{pmt}{(1+r)}+\frac{pmt}{(1+r)^2}+...+\frac{pmt}{(1+r)^n}$

( 2.20)

Современная стоимость 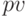- геометрическая прогрессия с 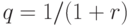a_0 = pmt /(1+r) , q=1/(1+r) , тогда

$pv=\frac{pmt}{(1+r)}[(1+r)^{-n}-1]/((1+r)^{-1}-1)$

( 2.21)

$pv=\frac{pmt}{r}[1-(1+r)^{-n}]$

( 2.22)

Размер платежа погашения ренты можно определить из (2.22)

$pmt=\frac{pv\cdot r}{[1-(1+r)^{-n}]}$

( 2.23)

Срок ренты, соответственно, и количество платежей при современной стоимости ренты 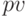, процентной ставке и платеже pmt из (2.23) равен

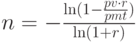$n=-\frac{\ln(1-\frac{pv\cdot r}{pmt})}{\ln(1+r)}$

( 2.24)

Ренты пренумерандо и постнумерандо

Рента пренумерандо - первый платеж поступает в начале первого периода, и рента постнумерандо – платеж поступает в конце периода. Вводится параметр , который учитывает тип ренты. Выражение для 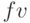(2.18), где учитывается тип ренты , будет иметь вид :

$pmt=\frac{[(1+r)^{-n}-1]}{r}\cdot (1+t\cdot r)$

( 2.25)

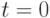где – тип ренты: t=0 или опущен - рента постнумерандо, выплата в конце периода, 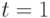t=1 – рента пренумерандо, выплата в начале периода. Для 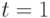t=1 появляется дополнительный член pmt[(1+r)^n-1] . Так учитывается более раннее поступление денег и удлинение на один период срока начисления процентов.

Для расчета будущего значения 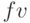используется формула (1.28), а для расчета периодического платежа pmt выражение

$pmt=r\cdot \frac{fv}{[(1+r)^n-1]\cdot (1+r\cdot t)}$

( 2.26)

В финансовых функциях тип ренты учитывается параметром [type] , который равен 0 (постнумерандо) и равен 1 (пренумерандо).

Примеры решения задач

Задача 2.3.

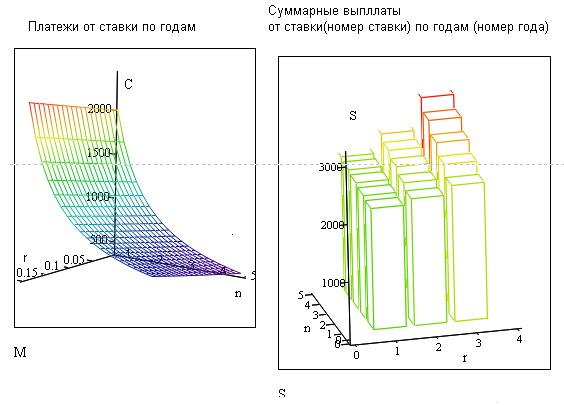
Предприятие предполагает получить кредит в банке 2000 тыс.руб. Кредит будет погашаться равными долями ежегодно, в конце года. Определить ежегодные платежи предприятия, если кредит берется на: 1, 2, 3, 4, 5 лет . Расчет провести для трех значений ставок :5%, 10%, 18%.

Решение (рис.2.3)

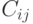Данные вводим в виде векторов r_i и n_j . Годовой платеж $C_{ij}$ . - матрица. При расчете используем формулу (2.23) и альтернативно финансовую функцию pmt (rate, nper, pv, [fv], [type]) , которая находит периодический постоянный платеж через данное число периодов nper по фиксированной процентной ставке rate , вкладу (заему) 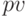, 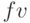- остаток долга, [type] – тип ренты. В квадратных скобках необязательные аргументы. Предполагаются распределенные во времени переходы денежных сумм от одного владельца к другому. 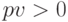Поскольку кредит – положительная величина поступление денежных средств к заемщику в начальный момент pv>0 , выплаты второму участнику операции соответствуют отрицательным платежам C < 0 .

Обозначим – платеж, –номер ставки, – номер года

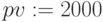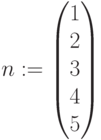
pv:=2000 , $r:=\begin{pmatrix} 5\% \\ 10\%\\ 18\% \end{pmatrix}$ , $n:=\begin{pmatrix} 1 \\ 2\\ 3 \\ 4 \\ 5 \end{pmatrix}$

Решение:

ORIGIN:=1 , i:=1..3 , j:=1..5

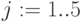
Платежи

$(C_{i,j}):=pv\cdot \frac{r_i}{[1-(1+r_i)^{-n_j}]}$

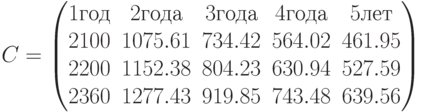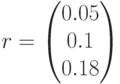
$C=\begin{pmatrix} 1 год & 2 года & 3 года & 4 года & 5 лет \\ 2100 & 1075.61 & 734.42 & 564.02 & 461.95 \\ 2200 & 1152.38 & 804.23 & 630.94 & 527.59 \\ 2360 & 1277.43 & 919.85 & 743.48 & 639.56 \end{pmatrix}$ , $r=\begin{pmatrix} 0.05 \\ 0.1 \\ 0.18 \end{pmatrix}$

Используем встроенную функцию pmt(r,n,pv,fv,t)

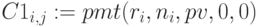
$C1_{i,j}:=pmt(r_i,n_i,pv,0,0)$

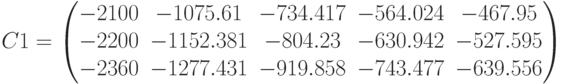
$C1=\begin{pmatrix} -2100 & -1075.61 & -734.417 & -564.024 & -467.95 \\ -2200 & -1152.381 & -804.23 & -630.942 & -527.595 \\ -2360 & -1277.431 & -919.858 & -743.477 & -639.556 \end{pmatrix}$

Суммарные выплаты для разных сроков

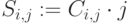
$S_{i,j}:=C_{i,j}\cdot j$

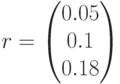
$C=\begin{pmatrix} 1 год & 2 года & 3 года & 4 года & 5 лет \\ 2100 & 2151 & 2203 & 2256 & 2310 \\ 2200 & 2305 & 2413 & 2524 & 2638 \\ 2360 & 2555 & 2760 & 2974 & 3198 \end{pmatrix}$ , $r=\begin{pmatrix} 0.05 \\ 0.1 \\ 0.18 \end{pmatrix}$