Визуализация пространственных реалистических сцен
Глобальная модель освещения с трассировкой лучей
Мы уже касались ранее понятия трассировки лучей при описании алгоритмов удаления невидимых граней. Теперь рассмотрим аналогичную процедуру в применении к моделям освещения. В предыдущей главе были описаны модели освещенности от некоторого источника света без учета того, что сами объекты сцены освещают друг друга посредством отраженных лучей. Метод излучательности, разработанный для диффузной модели освещенности, уже учитывает этот фактор.
Глобальная модель освещенности способна воспроизводить эффекты зеркального отражения и преломления лучей (прозрачность и полупрозрачность), а также затенение. Она является составной частью алгоритма удаления невидимых поверхностей методом трассировки.
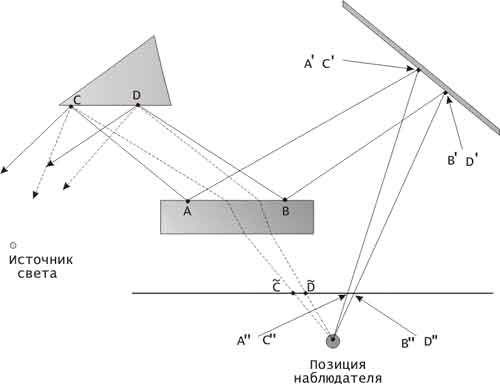
Если рассмотреть сцену, содержащую в числе прочих зеркальные и
полупрозрачные поверхности (рис. 10.3), то изображение будет включать,
во-первых, проекции самих объектов, освещенных одним или несколькими
источниками света. В некоторых своих частях эти объекты будут искажены
за счет преломления лучей в прозрачных и полупрозрачных телах. Во-
вторых, часть объектов будет отражаться зеркальными поверхностями, и
эти отражения появятся на проекциях зеркальных объектов. В
изображенной на рис. 10.3 сцене точки на поверхности призмы  видны
на картинной плоскости дважды: один раз - сквозь полупрозрачный
параллелепипед в виде точек
видны
на картинной плоскости дважды: один раз - сквозь полупрозрачный
параллелепипед в виде точек  , а второй раз - как дважды отраженные
невидимой поверхностью параллелепипеда и зеркалом
, а второй раз - как дважды отраженные
невидимой поверхностью параллелепипеда и зеркалом  . Параллелепипед в
данном случае частично обладает зеркальными свойствами.
. Параллелепипед в
данном случае частично обладает зеркальными свойствами.
Глобальная модель освещения для каждого пикселя изображения определяет его интенсивность. Будем для простоты считать, что все источники света - точечные. Сначала определяется непосредственная освещенность источниками без учета отражений от других поверхностей (вторичная освещенность): отслеживаются лучи, направленные ко всем источникам. Тогда наблюдаемая интенсивность (или отраженная точкой энергия) выражается следующим соотношением:
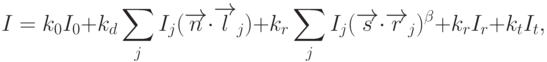
 - коэффициент фонового (рассеянного) освещения;
- коэффициент фонового (рассеянного) освещения;
 - коэффициент диффузного отражения;
- коэффициент диффузного отражения;
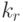 - коэффициент зеркального отражения;
- коэффициент зеркального отражения;
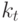 - коэффициент пропускания;
- коэффициент пропускания;
 - единичный вектор нормали к поверхности в точке;
- единичный вектор нормали к поверхности в точке;
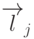 - единичный вектор, направленный к
- единичный вектор, направленный к  -му источнику света;
-му источнику света;
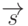 - единичный локальный вектор, направленный в точку наблюдения;
- единичный локальный вектор, направленный в точку наблюдения;
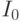 - интенсивность фонового освещения;
- интенсивность фонового освещения;
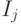 - интенсивность
- интенсивность  -го источника света;
-го источника света;
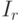 - интенсивность, приходящая по зеркально отраженному лучу;
- интенсивность, приходящая по зеркально отраженному лучу;
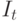 - интенсивность, приходящая по преломленному лучу.
- интенсивность, приходящая по преломленному лучу.
В алгоритме удаления невидимых линий трассировка луча продолжалась до первого пересечения с поверхностью. В глобальной модели освещения этим дело не ограничивается: осуществляется дальнейшая трассировка отраженного и преломленного лучей. Таким образом, происходит разветвление алгоритма в виде двоичного дерева. Процесс продолжается до тех пор, пока очередные лучи не останутся без пересечений. Отражение и преломление рассчитываются по законам геометрической оптики, которые уже рассматривались в предыдущей главе.
Пусть 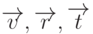 - направления падающего, отраженного и преломленного
лучей (рис. 10.4),
- направления падающего, отраженного и преломленного
лучей (рис. 10.4), 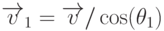 ,
,  - единичная внешняя нормаль,
- единичная внешняя нормаль, 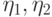 - коэффициенты
преломления сред, разделенных поверхностью. Тогда можно показать,
что
- коэффициенты
преломления сред, разделенных поверхностью. Тогда можно показать,
что
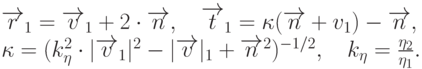
Двоичное дерево лучей можно строить по принципу "левое поддерево соответствует отраженному лучу, а правое - преломленному". После того как оно построено, можно вычислить интенсивность в точке. Для этого осуществляется обратный проход от вершин к корню, и при прохождении узлов интенсивность убывает.
Теоретически дерево может оказаться бесконечным, поэтому при его построении желательно задать максимальную глубину, чтобы избежать переполнения памяти компьютера.
Поскольку значительная часть лучей, исходящая от источников света и других поверхностей, не попадает в поле зрения наблюдателя, то отслеживать их все не имеет смысла. Поэтому для формирования изображения используется обратная трассировка, т. е. лучи отслеживаются в обратном порядке: от положения наблюдателя через все точки картинной плоскости к объектам и далее - по отраженным и преломленным лучам.


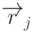 - отраженный
- отраженный