Проецирование пространственных сцен

Основные типы проекций

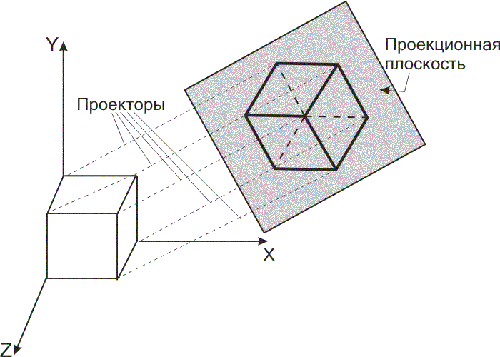
В математическом смысле проекции - это преобразования точек пространства размерности n в точки пространства размерности меньшей, чем n, или, как еще говорят, на подпространство исходного пространства. В компьютерной графике рассматриваются преимущественно проекции трехмерного пространства образа на двумерную картинную плоскость. Проекция трехмерного объекта, представленного в виде совокупности точек, строится при помощи прямых проецирующих лучей, которые называются проекторами и которые выходят из центра проекции, проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию.

Определенный таким образом класс проекций называют плоскими геометрическими проекциями, поскольку проецирование в этом случае производится на проекционную плоскость и в качестве проекторов используются прямые. Существуют и другие проекции, в которых проецирование осуществляется на криволинейные поверхности или же проецирование осуществляется не с помощью прямых (такие проекции используются, например, в картографии).

Следует отметить, что, приводя иллюстрации к данной главе, мы вынуждены использовать те же самые проекции, методы построения которых собираемся описать. Хочется надеяться, что материал из-за этого не будет выглядеть более неясным, чем при отсутствии рисунков.

Рис. 7.1. Проекция параллельным пучком лучей

увеличить изображение
Рис. 7.2. Центральная проекция

Плоские геометрические проекции подразделяются на два основных класса: центральные и параллельные. Различие между ними определяется соотношением между центром проекции и проекционной плоскостью. Если расстояние между ними конечно, то проекция будет центральной, если же оно бесконечно, то проекция будет параллельной. Параллельные проекции названы так потому, что центр проекции бесконечно удален и все проекторы параллельны. При описании центральной проекции мы явно задаем ее центр проекции, в то время как, определяя параллельную проекцию, мы указываем направление проецирования. На рис. 7.1 и 7.2 показаны две различные проекции одного и того же отрезка, а также проекторы, проходящие через его конечные точки. Поскольку проекция отрезка сама является отрезком, то достаточно спроецировать одни лишь конечные точки и соединить их.

Центральная проекция порождает визуальный эффект, аналогичный тому, к которому приводят фотографические системы или зрительная система человека, и поэтому используется в случаях, когда желательно достичь определенной степени реалистичности. Этот эффект называется перспективным укорачиванием: по мере увеличения расстояния от центра до объекта размер получаемой проекции уменьшается. Это, с другой стороны, означает, что хотя центральная проекция объектов является реалистичной, она оказывается непригодной для представления точной формы и размеров объектов: из проекции нельзя получить информацию об относительных расстояниях; углы сохраняются только на тех гранях объекта, которые параллельны проекционной плоскости; проекции параллельных линий в общем случае не параллельны. Так, при центральной проекции куба в большинстве случаев мы получаем картину, вообще не имеющую параллельных отрезков.

Параллельная проекция порождает менее реалистичное изображение, поскольку отсутствует перспективное укорачивание, хотя при этом могут иметь место различные постоянные укорачивания вдоль каждой из осей. Проекция фиксирует истинные размеры (с точностью до скалярного множителя), и параллельные прямые остаются параллельными. Как и в случае центральной проекции, углы сохраняются только на тех гранях объекта, которые параллельны проекционной плоскости.

Параллельные проекции

Параллельные проекции разделяются на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости. Если эти направления совпадают, т.е. направление проецирования является нормалью к проекционной плоскости, то проекция называется ортографической. Если же проекторы не ортогональны к проекционной плоскости, то проекция называется косоугольной.

Рис. 7.3. Ортографические проекции

В инженерной графике наиболее широко используемыми видами ортографических проекций являются вид спереди, вид сверху (план) и вид сбоку, в которых проекционная плоскость перпендикулярна главным координатным осям, совпадающим вследствие этого с направлением проецирования (рис. 7.3). Поскольку каждая проекция отображает лишь одну сторону объекта, часто совсем непросто представить себе пространственную структуру проецируемого объекта, даже если рассматривать сразу несколько проекций одного и того же объекта. Но тем не менее такие чертежи позволяют определять реальные размеры объекта.

В случае аксонометрических ортографических проекций используются проекционные плоскости, не перпендикулярные главным координатным осям, поэтому на них изображается сразу несколько сторон объекта, так же как и при центральном проецировании, однако в аксонометрии укорачивание постоянно, тогда как в случае центральной проекции оно связано с расстоянием от центра проекции. При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; расстояния же можно измерить вдоль каждой из главных координатных осей (в общем случае с различными масштабными коэффициентами).

увеличить изображение
Рис. 7.4. Изометрическая проекция

Аксонометрические проекции подразделяются на три группы в соответствии с расположением проекционной плоскости по отношению к осям координат. Если нормаль к проекционной плоскости образует три различных угла с осями, то проекция называется триметрической ( триметрией ). Если два из этих углов одинаковы, то получаем диметрическую проекцию ( диметрию ). И, наконец, если все три угла равны между собой, то проекция называется изометрической ( изометрией ). Изометрическая проекция обладает тем свойством, что все три главные координатные оси одинаково укорачиваются. Поэтому можно проводить измерения вдоль направления осей с одним и тем же масштабом (отсюда название: "изо", что означает "равно", и "метрия" - "измерение"). Кроме того, главные координатные оси проецируются так, что их проекции составляют равные углы друг с другом (рис. 7.4).

Косоугольные проекции также являются параллельными, причем проекционная плоскость перпендикулярна главной координатной оси. Сторона объекта, параллельная этой плоскости, проецируется так, что можно измерять углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Мы коснемся только двух наиболее часто используемых косоугольных проекций: проекции кавалье ( cavalier ) и кабине ( cabinet ). В отечественной практике эти проекции называют горизонтальной косоугольной изометрией и кабинетной проекцией.

Рис. 7.5. Горизонтальная косоугольная изометрия (а) и кабинетная проекция (б)

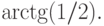В проекции горизонтальной косоугольной изометрии направление проецирования составляет с плоскостью угол 45 . В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т.е. укорачивание отсутствует (рис. 7.5a). Кабинетная проекция имеет направление проецирования, которое составляет с проекционной плоскостью угол При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют 1/2 их действительной длины, что более соответствует нашему визуальному опыту, поэтому изображение выглядит более реалистично (рис. 7.5b).