Закрашивание. Рендеринг полигональных моделей
Закраска граней
Плоское закрашивание
Если предположить, что источник света находится на бесконечности, то лучи света, падающие на поверхность, параллельны между собой. Если к этому добавить условие, что наблюдатель находится в бесконечно удаленной точке, то эффектом ослабления света с увеличением расстояния от источника также можно пренебречь. Кроме того, такое положение наблюдателя означает еще и то, что векторы, направленные от разных точек поверхности к наблюдателю, также будут параллельны. При выполнении всех этих условий, как следует из формулы (9.6), плоская грань во всех точках имеет одинаковую интенсивность освещения, поэтому она закрашивается одним цветом. Такое закрашивание называется плоским.
Если мы аппроксимируем некоторую гладкую поверхность многогранником, то при плоском закрашивании неизбежно проявятся ребра, поскольку соседние грани с различными направлениями нормалей имеют разный цвет. Эффект полос Маха дополнительно усиливает этот недостаток. Для его устранения при использовании этого способа закрашивания можно лишь увеличить число граней многогранника, что приводит к увеличению вычислительной сложности алгоритма.
Закраска методом Гуро
Один из способов устранения дискретности интенсивностей закрашивания был предложен Гуро. Его метод заключается в том, что используются не нормали к плоским граням, а нормали к аппроксимируемой поверхности, построенные в вершинах многогранника. После этого вычисляются интенсивности в вершинах, а затем во всех внутренних точках многоугольника выполняется билинейная интерполяция интенсивности.
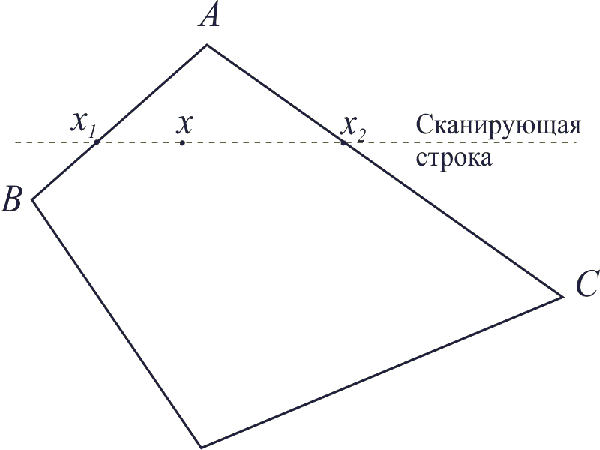
Метод сочетается с алгоритмом построчного сканирования. После того как грань отображена на плоскость изображения, для каждой сканирующей строки определяются ее точки пересечения с ребрами. В этих точках интенсивность вычисляется с помощью линейной интерполяции интенсивностей в вершинах ребра. Затем для всех внутренних точек многоугольника, лежащих на сканирующей строке, также вычисляется интенсивность методом линейной интерполяции двух полученных значений. На рис. 9.5 показан плоский многоугольник с вычисленными значениями интенсивностей в вершинах.
Пусть  - интенсивности в вершинах
- интенсивности в вершинах 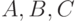 ,
, 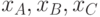 - горизонтальные координаты
этих точек. Тогда в точках пересечения сканирующей строки с ребрами
многоугольника интенсивности можно вычислить по формулам
интерполяции:
- горизонтальные координаты
этих точек. Тогда в точках пересечения сканирующей строки с ребрами
многоугольника интенсивности можно вычислить по формулам
интерполяции:
 |
( 9.7) |
 получаем путем интерполяции
значений на концах отрезка:
получаем путем интерполяции
значений на концах отрезка: |
( 9.8) |
К недостаткам метода Гуро следует отнести то, что он хорошо работает только с диффузной моделью отражения. Форма бликов на поверхности и их расположение не могут быть адекватно воспроизведены при интерполяции на многоугольниках. Кроме того, есть проблема построения нормалей к поверхности. В алгоритме Гуро нормаль в вершине многогранника вычисляется путем усреднения нормалей к граням, примыкающим к этой вершине. Такое построение сильно зависит от характера разбиения.
Закраска методом Фонга
Фонг предложил вместо интерполяции интенсивностей произвести интерполяцию вектора нормали к поверхности на сканирующей строке. Этот метод требует больших вычислительных затрат, поскольку формулы интерполяции (9.6)–(9.7) применяются к трем компонентам вектора нормали, но зато дает лучшую аппроксимацию кривизны поверхности. Поэтому зеркальные свойства поверхности воспроизводятся гораздо лучше.
Нормали к поверхности в вершинах многогранника вычисляются так же, как и в методе Гуро. А затем выполняется билинейная интерполяция в сочетании с построчным сканированием. После построения вектора нормали в очередной точке вычисляется интенсивность.
Этот метод позволяет устранить ряд недостатков метода Гуро, но не все. В частности, эффект полос Маха в отдельных случаях в методе Фонга бывает даже сильнее, хотя в подавляющем большинстве случаев аппроксимация Фонга дает лучшие результаты. На рис. 9.6 приведены результаты закрашивания поверхности вращения, аппроксимированной многогранником, который составлен из треугольных граней: a) - плоское закрашивание, b) - закрашивание по методу Гуро, c) - закрашивание по методу Фонга. Первый из вариантов дает изображение ребристой поверхности с очень контрастными переходами от одной грани к другой. Вторая модель дает более гладкое изображение, но в районе бликов отчетливо наблюдаются линии ребер, хотя и сглаженные. Третий вариант получился наиболее гладким, зеркальные блики имеют достаточно реалистичную форму.