Удаление невидимых поверхностей и линий
Метод трассировки лучей
Главная идея этого алгоритма была предложена в 1968 г. А.Аппелем, а первая реализация была выполнена в 1971 г.
Наблюдатель видит любой объект посредством испускаемого неким источником света, который падает на этот объект, отражается или преломляется согласно законам оптики и затем каким-то путем доходит до глаза наблюдателя. Из огромного множества лучей света, выпущенных источником, лишь небольшая часть дойдет до наблюдателя. Следовательно, отслеживать пути лучей в таком порядке неэффективно с точки зрения вычислений. Аппель предложил отслеживать (трассировать) лучи в обратном направлении, т.е. от наблюдателя к объекту. В первой реализации этого метода трассировка прекращалась, как только луч пересекал поверхность видимого непрозрачного объекта; т.е. луч использовался только для обработки скрытых или видимых поверхностей. Впоследствии были реализованы алгоритмы трассировки лучей с использованием более полных моделей освещения с учетом эффектов отражения одного объекта от поверхности другого, преломления, прозрачности и затенения.
В этом алгоритме предполагается, что сцена уже преобразована в
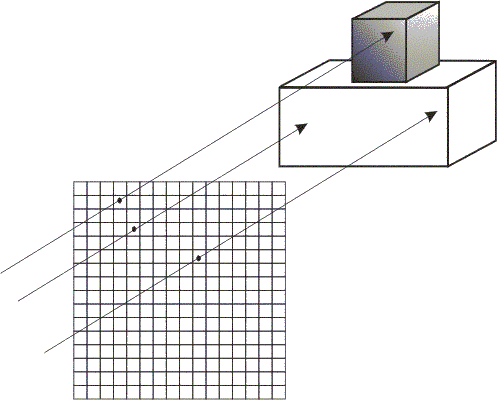
пространство изображения. Если используется ортографическая проекция,
то точка зрения или наблюдатель находится в бесконечности на
положительной полуоси 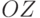 . В этом случае все световые лучи, идущие от
наблюдателя, параллельны оси (рис. 6.7). Каждый луч проходит через
пиксель растра до сцены. Траектория каждого луча отслеживается, чтобы
определить, какие именно объекты сцены, если таковые существуют,
пересекаются с данным лучом. Необходимо проверить пересечение каждого
объекта сцены с каждым лучом. Если луч пересекает объект, то
определяются все возможные точки пересечения луча и объекта. Можно
получить большое количество пересечений, если рассматривать много
объектов. Эти пересечения упорядочиваются по глубине. Пересечение с
максимальным значением
. В этом случае все световые лучи, идущие от
наблюдателя, параллельны оси (рис. 6.7). Каждый луч проходит через
пиксель растра до сцены. Траектория каждого луча отслеживается, чтобы
определить, какие именно объекты сцены, если таковые существуют,
пересекаются с данным лучом. Необходимо проверить пересечение каждого
объекта сцены с каждым лучом. Если луч пересекает объект, то
определяются все возможные точки пересечения луча и объекта. Можно
получить большое количество пересечений, если рассматривать много
объектов. Эти пересечения упорядочиваются по глубине. Пересечение с
максимальным значением  представляет видимую поверхность для данного
пикселя. Атрибуты этого объекта используются для определения
характеристик пикселя.
представляет видимую поверхность для данного
пикселя. Атрибуты этого объекта используются для определения
характеристик пикселя.
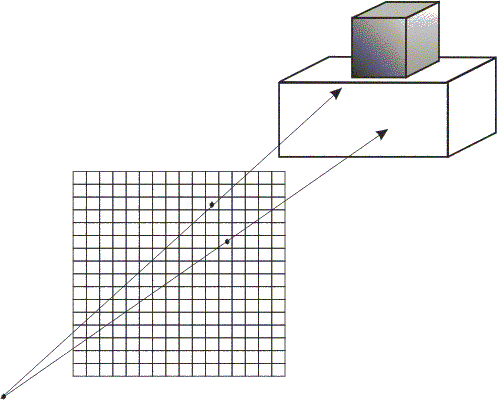
Если точка зрения находится не в бесконечности (перспективная
проекция), алгоритм трассировки лучей лишь незначительно усложняется.
Здесь предполагается, что наблюдатель по-прежнему находится на
положительной полуоси 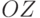 . Картинная плоскость, т.е. растр,
перпендикулярна оси
. Картинная плоскость, т.е. растр,
перпендикулярна оси 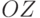 , как показано на рис. 6.8.
, как показано на рис. 6.8.
Наиболее важным и трудоемким элементом этого алгоритма является процедура определения пересечений, поскольку эта задача отнимает наибольшую часть времени всей работы алгоритма. Поэтому эффективность методов поиска особенно важна. Объекты сцены могут состоять из набора плоских многоугольников, многогранников или тел, ограниченных замкнутыми параметрическими поверхностями. Для ускорения поиска важно иметь эффективные критерии, позволяющие исключить из процесса заведомо лишние объекты.
Одним из способов сокращения числа пересекаемых объектов является погружение объектов в выпуклую оболочку - сферическую или в форме параллелепипеда. Поиск пересечения с такой оболочкой очень прост, и если луч не пересекает оболочки, то не нужно больше искать пересечений этого объекта с лучом.
Особенно просто выполняется тест на пересечение со сферической оболочкой (в "Геометрические преобразования" были рассмотрены задачи о пересечении луча со сферой и плоскостью). Несколько большего объема вычислений требует задача о пересечении с прямоугольным параллелепипедом, поскольку необходимо проверить пересечение луча по меньшей мере с тремя бесконечными плоскостями, ограничивающими прямоугольную оболочку. Поскольку точки пересечения могут оказаться вне граней этого параллелепипеда, для каждой из них следует, кроме того, произвести проверку на попадание внутрь. Следовательно, для трех измерений тест с прямоугольной оболочкой оказывается более медленным, чем тест со сферической оболочкой.
После выполнения этих первичных тестов начинается процесс поиска пересечений с объектами, попавшими в список потенциально видимых. При этом задача формирования изображения не исчерпывается нахождением самой точки пересечения: если мы учитываем эффекты отражения и преломления, необходимо отслеживать дальнейший путь луча, для чего, как правило, требуется восстановить нормаль к поверхности, а также определить направление отраженного или преломленного луча. В связи со всеми этими задачами важно выбрать достаточно удобные аппроксимации поверхностей, составляющих сцену. Определение атрибутов пикселя, выводимого в конечном итоге на экран, зависит от выбора модели освещения, о чем более подробно будет рассказано в последующих лекциях.
Алгоритм трассировки лучей для простых непрозрачных поверхностей можно представить следующим образом.
Создать список объектов, содержащий:
- полное описание объекта: тип, поверхность, характеристики, тип оболочки и т.п.;
- описание оболочки: центр и радиус для сферы или шесть значений для параллелепипеда
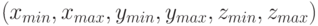 .
.
Для каждого трассируемого луча:
Выполнить для каждого объекта трехмерный тест на пересечение с оболочкой. Если луч пересекает эту оболочку, то занести объект в список активных объектов.
Если список активных объектов пуст, то изобразить данный пиксель с фоновым значением цвета и продолжать работу. В противном случае для каждого объекта из списка активных объектов:
- Найти пересечения со всеми активными объектами.
- Если список пересечений пуст, то изобразить данный пиксель с фоновым значением цвета.
- В противном случае в списке пресечений найти ближайшее к наблюдателю (с максимальным значением
 ) и определить атрибуты точки.
) и определить атрибуты точки. - Изобразить данный пиксель, используя найденные атрибуты пересеченного объекта и соответствующую модель освещенности.
В настоящее время алгоритм трассировки, несмотря на вычислительную сложность, стал очень популярен, особенно в тех случаях, когда время формирования изображения не очень существенно, но хочется добиться как можно большей реалистичности изображения.
Вопросы и упражнения
- В чем заключается суть удаления невидимых линий и поверхностей?
- В каком пространстве работает алгоритм Робертса?
- Для каких объектов примеряется алгоритм Робертса?
- Что представляет собой вектор-столбец обобщенной матрицы описания многогранника?
- Как интерпретируется выражение
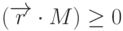 (
(  - обобщенная матрица) в алгоритме Робертса?
- обобщенная матрица) в алгоритме Робертса? - В каком пространстве работает алгоритм Варнока?
- Какие типы расположения многоугольника относительно окна рассматриваются в алгоритме Варнока?
- Который из шести шагов алгоритма решает задачу об удалении невидимых поверхностей?
- В каком пространстве работает алгоритм Вейлера-Азертона?
- В чем принципиальное отличие алгоритма Вейлера-Азертона от алгоритма Варнока?
- Какое обобщение алгоритма Вейлера-Азертона предложил Кэтмул?
- Кем предложен алгоритм Z-буфера?
- В чем недостатки алгоритма Z-буфера?
- На чем основаны методы приоритетов?
- Для какого вида изображения разработан метод художника?
- Для какого вида изображения разработан метод плавающего горизонта?
- Что общего между алгоритмом построчного сканирования и методом Z-буфера?
- В чем состоит идея метода трассировки?
- Какие бывают виды трассировки?
- Какие приемы используются для повышения эффективности алгоритма трассировки?