Геометрические преобразования
Аналитическое представление кривых и поверхностей
Пусть на плоскости задана декартова система координат.
Кривая на плоскости - это геометрическое место точек  , удовлетворяющих уравнению
, удовлетворяющих уравнению
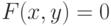 |
( 3.10) |
 - функция двух переменных. Ясно, что далеко не каждая функция
будет задавать линию. Так, например, уравнению
- функция двух переменных. Ясно, что далеко не каждая функция
будет задавать линию. Так, например, уравнению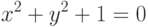
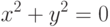
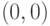 .
.Для аналитического представления кривой во многих случаях удобнее
задавать кривую параметрическими уравнениями, используя
вспомогательную переменную (параметр)  :
:
![x=\varphi(t), \quad y=\psi(t), t \in [a,b],](/sites/default/files/tex_cache/397b34c804d5bb4019467803b840c0dc.png) |
( 3.11) |
 и
и  - непрерывные функции на заданном интервале изменения
параметра. Если функция
- непрерывные функции на заданном интервале изменения
параметра. Если функция  такова, что можно выразить
такова, что можно выразить  через
через 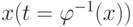 , то
от параметрического представления кривой легко перейти к уравнению
(3.10):
, то
от параметрического представления кривой легко перейти к уравнению
(3.10):
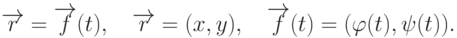
Отрезок прямой представляет собой частный случай кривой, причем параметрическое представление его может иметь вид
![x=t, \quad y=at+b, \quad t \in[t_1,t_2]](/sites/default/files/tex_cache/957020362cc7290b763a4a222c7a7310.png)
![x=at+b, y=t, t\in[t_1,t_2]](/sites/default/files/tex_cache/b7b8eb650bd38f86d5c887b47291afd4.png)
Окружность радиуса  с центром в точке
с центром в точке 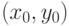 может быть представлена
параметрическими уравнениями
может быть представлена
параметрическими уравнениями
![x=x_0+r\cdot\cos t, \quad y=y_0+r\cdot\sin t, t\in[0,2\pi].](/sites/default/files/tex_cache/32e3749e1c1de926dfe973584947cd4b.png)
Перейдем к трехмерному пространству с заданной декартовой системой координат.
Поверхность в пространстве - это геометрическое место точек 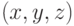 ,
удовлетворяющих уравнению вида
,
удовлетворяющих уравнению вида
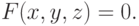 |
( 3.12) |
Так же как и в случае кривой на плоскости, не всякая функция  описывает какую-либо поверхность. Например, уравнению
описывает какую-либо поверхность. Например, уравнению
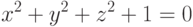
![x=\varphi(u,v), \quad y=\psi(u,v), \quad z=\zeta(u,v), \quad u\in[a,b], \quad v\in[c,d].](/sites/default/files/tex_cache/4d15c937f8a4516f8f9819ed359eba9b.png) |
( 3.13) |
Например, сфера радиуса  с центром в точке
с центром в точке  может быть задана
уравнением
может быть задана
уравнением
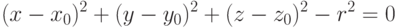
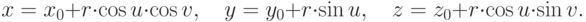
Кривую в пространстве можно описать как пересечение двух поверхностей, т.е. с помощью системы уравнений
 |
( 3.14) |
![x=\varphi(t), \quad y=\psi(t), z=\zeta(t), \quad t\in[a,b].](/sites/default/files/tex_cache/cb100da2b3661b2e299cb3620f2289ec.png) |
( 3.15) |

