|
Здравствуйте, через какое время будет защитана загруженная курсовая? |
Использование функций
Финансовые вычисления
О финансовых функциях
Финансовые функции используют в планово-экономических расчетах.
Расчет амортизационных отчислений
Для расчета амортизационных отчислений необходимо знать, по крайней мере, три параметра:
- начальная стоимость имущества;
- остаточная стоимость по окончании эксплуатации;
- продолжительность эксплуатации.
Для расчета амортизационных отчислений могут быть использованы различные принципы и методики. В зависимости от этого могут быть применены и различные функции.
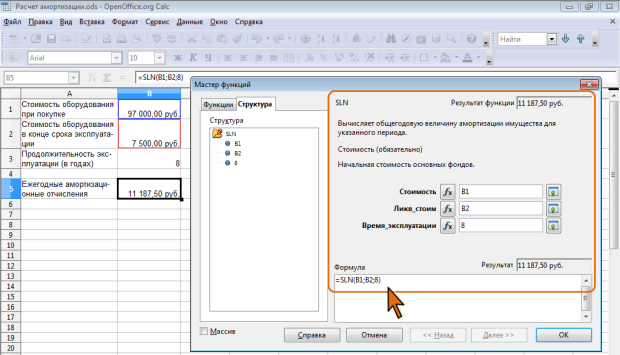
В простейшем случае амортизация разносится равномерно на каждый год эксплуатации имущества. Для расчета величины амортизационных отчислений в этом случае используют функцию SLN. Синтаксис функции:
SLN(Стоимость; Ликв_стоим; Время_эксплуатации),
где: Стоимость – начальная стоимость актива. Ликв_стоим – стоимость актива в конце периода амортизации. Время эксплуатации – период амортизации, который определяет количество периодов для актива.
Например, приобретено оборудование стоимостью 97000 руб. Продолжительность эксплуатации оборудования – 8 лет. Остаточная стоимость – 7500 руб. Величина амортизационных отчислений составит 11187,50 руб. за каждый и любой год эксплуатации ( рис. 7.9).
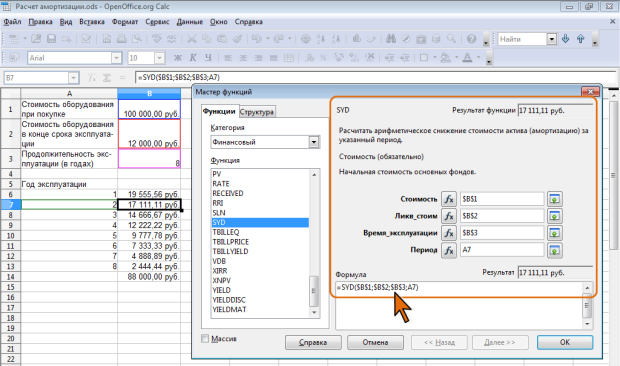
В более сложном случае необходимо учитывать, что стоимость имущества в процессе его эксплуатации уменьшается. Следовательно, с каждым годом эксплуатации должны уменьшаться и амортизационные отчисления. Однако суммарно величина амортизационных отчислений должна составить разницу между начальной и остаточной стоимостью имущества. Для расчета величины амортизационных отчислений в этом случае используют функцию SYD. Синтаксис функции:
SYD(Стоимость; Ликв_стоим; Время_эксплуатации; Период),
где: Стоимость – начальная стоимость актива. Ликв_стоим – стоимость актива после амортизации. Время_эксплуатации – период, в течение которого стоимость актива амортизируется. Период – период, для которого рассчитывается амортизация.
Например, приобретено оборудование стоимостью 100000 руб. Продолжительность эксплуатации оборудования – 8 лет. Остаточная стоимость – 12000 руб. Величина амортизационных отчислений за первый год эксплуатации составит 19 555,56 руб., за второй год – 17 111,11 руб. и т. д. ( рис. 7.10).
Анализ инвестиций
Использование сложных процентов необходимо при вычислении доходности вкладов (инвестиций), сумм платежей по кредитам, сумм страховых платежей и т. п.
Во всех этих случаях для расчета необходимо знать, по крайней мере, три параметра:
- процентная ставка за период;
- общее число периодов платежей;
- выплата, производимая в каждый период или общая сумма.
Все аргументы, означающие денежные средства, которые должны быть выплачены, представляются отрицательными числами; денежные средства, которые должны быть получены, представляются положительными числами.
Расчет суммы вклада (величины займа)
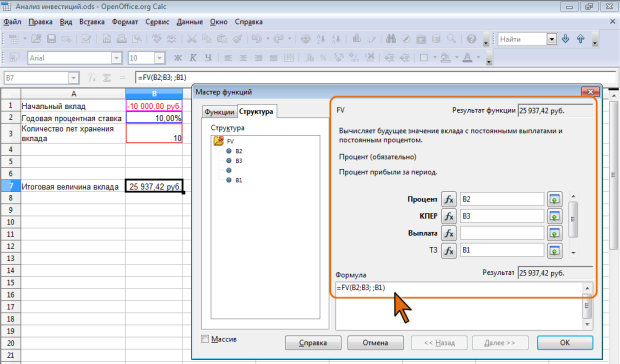
В простейших случаях для расчета можно использовать функцию FV. Эта функция вычисляет для будущего момента времени величину вложения, которое образуется в результате единовременного вложения и/или регулярных периодических вложений под определенный процент. Эту же функцию можно использовать для вычисления возможной величины займа под определенный процент, при определенных регулярных периодических выплатах по погашению займа. Синтаксис функции:
FV(Процент; КПЕР; Выплата; ТЗ; Тип),
где: Процент – процентная ставка за период. КПЕР – общее число платежей. Выплата – выплата, производимая в каждый период и не меняющаяся за все время выплаты (если аргумент опущен, он полагается равным 0). ТЗ (необязательно) – текущая денежная стоимость инвестиции. Тип (необязательно) – срок выплаты в начале или конце периода (число 0 или 1, обозначающее, когда должна производиться выплата. 0 или опущен – в конце периода, 1 – в начале периода).
При создании формулы следует устанавливать одинаковую размерность периода для процентной ставки и числа платежей. Например, если платежи производятся один раз в год, то и процентная ставка должна быть дана в годовом исчислении, а если платежи производятся ежемесячно, то должна быть задана месячная процентная ставка.
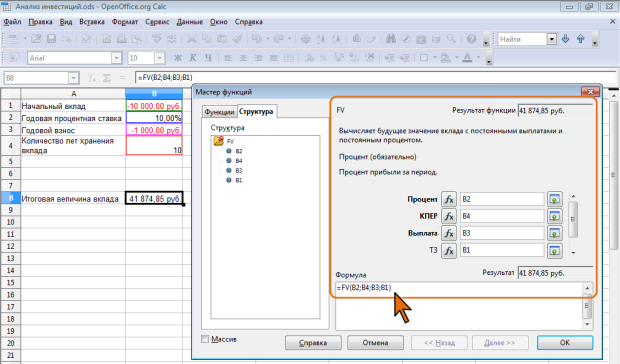
Например, необходимо рассчитать будущую сумму вклада в размере 10000 руб., внесенного на 10 лет с ежегодным начислением 10% ( рис. 7.11). Или будущую сумму вклада при тех же условиях, но с ежегодным внесением 1000 руб. ( рис. 7.12).
увеличить изображение
Рис. 7.12. Расчет величины вклада с начальным взносом при регулярном пополнении
Результат вычисления – в первом случае – 25937,4 руб., во втором – 41874,85руб.
Расчет процентных платежей
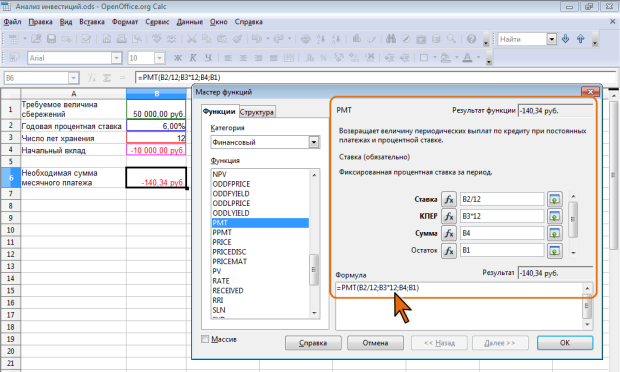
В зависимости от порядка расчетов могут быть использованы различные функции. В простейших случаях для расчета можно использовать функцию PMT. Функция PMT вычисляет размер периодических выплат, необходимых для погашения займа, полученного под определенный процент, за определенный срок. Эту же функцию можно использовать для вычисления величины регулярных вложений под определенный процент, необходимых для достижения определенной величины вклада за определенный срок. Синтаксис функции:
PMT(Ставка; КПЕР; Сумма; Остаток; Тип),
где: Ставка – процентная ставка за период. КПЕР – общее число платежей. Сумма – выплата, производимая в каждый период и не меняющаяся за все время выплаты. Остаток (необязательно) – требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0 ). Тип (необязательно) – срок периодических платежей (число 0 или 1, обозначающее, когда должна производиться выплата. 0 или опущен – в конце периода. 1 – в начале периода).
При создании формулы следует устанавливать одинаковую размерность периода для процентной ставки и числа платежей. Например, если выплаты производятся один раз в год, то и процентная ставка должна быть дана в годовом исчислении, а если выплаты производятся ежемесячно, то должна быть задана месячная процентная ставка.
Например, необходимо рассчитать величину ежемесячного вложения под 6 % годовых, которое через 12 лет составит сумму вклада 50000 руб. ( рис. 7.13)
Результат вычисления получается отрицательным (-140,34 руб.) поскольку эту сумму необходимо выплачивать.