|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Квантовые процессоры на переходах Джозефсона
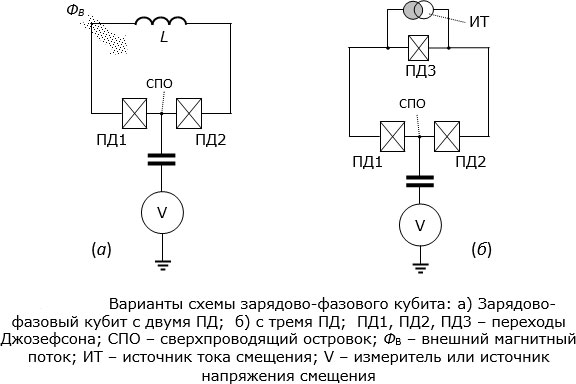
Зарядово-фазовые кубиты
Зарядово-фазовыми называют кубиты с ПД, в которых не выполняются ни условие  , ни условие
, ни условие 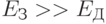 , т.е. "джозефсоновская" и зарядовая энергии имеют один порядок величины. Два варианта принципиальной схемы таких кубитов показаны на
рис.
10.7. Изолированный сверхпроводящий островок СПО соединен здесь с двумя одинаковыми ПД (ПД1 и ПД2), включенными в сверхпроводящий контур. Схему слева в англоязычных публикациях называют еще "the single Cooper pair transistor" (SCT).
, т.е. "джозефсоновская" и зарядовая энергии имеют один порядок величины. Два варианта принципиальной схемы таких кубитов показаны на
рис.
10.7. Изолированный сверхпроводящий островок СПО соединен здесь с двумя одинаковыми ПД (ПД1 и ПД2), включенными в сверхпроводящий контур. Схему слева в англоязычных публикациях называют еще "the single Cooper pair transistor" (SCT).
В случае, когда параметры ПД таковы, что  , эта схема работает в "зарядовом" режиме. Тогда ее применяют для контроля зарядового состояния кубита путем измерения сигналов из индуктивности
, эта схема работает в "зарядовом" режиме. Тогда ее применяют для контроля зарядового состояния кубита путем измерения сигналов из индуктивности  . В общем же случае, когда энергии
. В общем же случае, когда энергии  и
и  близки, ни величина заряда на островке, ни магнитный поток через сверхпроводящий контур не определены, так как соответствующие им операторы в уравнении Шредингера для этой структуры не коммутируют между собой. Это – типично квантово-механическое явление, аналогичное тому, как электрон в атоме не имеет ни определенной координаты, ни определенного импульса.
близки, ни величина заряда на островке, ни магнитный поток через сверхпроводящий контур не определены, так как соответствующие им операторы в уравнении Шредингера для этой структуры не коммутируют между собой. Это – типично квантово-механическое явление, аналогичное тому, как электрон в атоме не имеет ни определенной координаты, ни определенного импульса.
Система является устойчивой лишь при определенных дискретных значениях энергии, два нижайших из которых и принимаются за базовые состояния зарядово-фазового кубита. Неопределенность заряда и магнитного потока сквозь сверхпроводящий контур усложняет экспериментальное изучение таких кубитов. Но их преимуществом является то, что их состоянием можно управлять как путем изменения внешнего магнитного потока  , так и путем изменения напряжения смещения
, так и путем изменения напряжения смещения  , а также путем изменения тока смещения в схеме на
рис.
10.7.б. Это создает дополнительные возможности при объединении многих кубитов в систему.
, а также путем изменения тока смещения в схеме на
рис.
10.7.б. Это создает дополнительные возможности при объединении многих кубитов в систему.
Манипулирование квантовым состоянием сверхпроводящих кубитов
Выше уже отмечалось, что записывать и считывать информацию в случае зарядовых кубитов можно с помощью специальных электродов, расположенных вблизи от изолированных сверхпроводящих островков (напр., непосредственно под ними), а в случае потоковых кубитов – с помощью внешнего магнитного поля и специального сквида, связанного с данным кубитом через магнитный поток. Мы отмечали и то, что магнитная связь может быть и не непосредственной, а через рамку из сверхпроводника, одно отверстие которой расположено рядом, над или под кубитом, а другое – рядом с измерительным сквидом или с источником импульсов тока записи/считывания.
Манипулировать сверхпроводящими кубитами на ПД можно также с помощью импульсов сверхвысокочастотного (СВЧ) электромагнитного поля. При теоретическом исследовании такого манипулирования к стационарному гамильтониану сверхпроводящего кубита добавляют потенциал взаимодействия кубита с электромагнитным полем и получают нестационарное уравнение Шредингера, описывающее эволюцию системы во времени. Теоретический анализ показал и экспериментальные исследования подтвердили, что сверхпроводящий кубит на ПД в этом взаимодействии ведет себя как высокодобротный колебательный контур ("осциллятор"). Он взаимодействует лишь с теми частотными компонентами электромагнитного поля, которые отвечают собственным резонансным частотам кубита
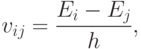 |
( 10.7) |
 -го разрешенного энергетического уровня (
-го разрешенного энергетического уровня (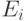 ) на
) на  -й (
-й (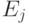 ). Если, например, кубит находится в базовом состоянии
). Если, например, кубит находится в базовом состоянии 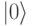 и на него начинает действовать электромагнитное поле с резонансной частотой
и на него начинает действовать электромагнитное поле с резонансной частотой 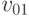 , которая соответствует энергии перехода в состояние
, которая соответствует энергии перехода в состояние 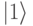 , то под влиянием этого поля происходит вполне определенная квантовая эволюция, геометрической интерпретацией которой является поворот вектора состояния на сфере Блоха. Это аналогично действию поперечного переменного магнитного поля на спиновые кубиты. В частности, вероятность
, то под влиянием этого поля происходит вполне определенная квантовая эволюция, геометрической интерпретацией которой является поворот вектора состояния на сфере Блоха. Это аналогично действию поперечного переменного магнитного поля на спиновые кубиты. В частности, вероятность  считать с кубита состояние
считать с кубита состояние 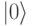 в результате действия резонансного СВЧ поля быстро уменьшается со временем от 1 до 0.
в результате действия резонансного СВЧ поля быстро уменьшается со временем от 1 до 0.СВЧ импульсы с длительностью, при которой вероятность пребывания кубита в состояниях 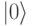 и
и 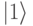 становится одинаковой (
становится одинаковой (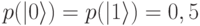 ), - называют "
), - называют " -импульсами". Такие значения вероятностей означают, что после воздействия
-импульсами". Такие значения вероятностей означают, что после воздействия  -импульса кубит, который пребывал в состоянии
-импульса кубит, который пребывал в состоянии 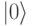 , оказывается в смешанном состоянии с волновой функцией
, оказывается в смешанном состоянии с волновой функцией 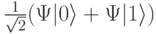 .
При дальнейшем взаимодействии с СВЧ импульсом квантовое состояние кубита эволюционирует в направлении базового состояния
.
При дальнейшем взаимодействии с СВЧ импульсом квантовое состояние кубита эволюционирует в направлении базового состояния 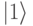 . СВЧ импульсы с длительностью, при которой кубит окончательно переходит в состояние
. СВЧ импульсы с длительностью, при которой кубит окончательно переходит в состояние 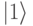 , т.е.
, т.е. 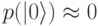 , а
, а 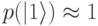 , – называют "
, – называют " -импульсами". Продолжительность
-импульсами". Продолжительность  - и
- и  -импульсов зависит от амплитуды СВЧ колебаний: чем она больше, тем быстрее происходит изменение состояния и тем короче
-импульсов зависит от амплитуды СВЧ колебаний: чем она больше, тем быстрее происходит изменение состояния и тем короче  -импульс во времени.
-импульс во времени.
В случае потоковых кубитов наиболее эффективное взаимодействие имеет место тогда, когда в создаваемом электромагнитном поле вектор магнитной индукции  направлен перпендикулярно к плоскости сверхпроводящего контура, а в случае зарядовых кубитов – тогда, когда вектор напряженности электрического поля
направлен перпендикулярно к плоскости сверхпроводящего контура, а в случае зарядовых кубитов – тогда, когда вектор напряженности электрического поля 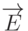 ориентирован перпендикулярно к плоскости ПД.
ориентирован перпендикулярно к плоскости ПД.
Поскольку в потоковых кубитах и сквидах положение энергетических уровней зависит от внешнего магнитного поля или/и от тока смещения, то с помощью обоих этих факторов можно несколько изменять резонансные частоты и тем самым управлять извне результатом взаимодействия с электромагнитным полем. Экспериментальные исследования полностью подтвердили теоретические выводы.
Таким образом, действуя на сверхпроводящий кубит СВЧ импульсами резонансной частоты и нужной продолжительности, можно выполнять над ним квантовую логическую операцию поворота вектора состояния кубита на любой соответствующий угол.
Рассмотрим теперь случай взаимодействия СВЧ электромагнитных импульсов с парой потоковых кубитов, между которыми имеет место слабая индуктивная связь (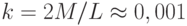 , где
, где  – собственная индуктивность каждого кубита,
– собственная индуктивность каждого кубита,  – их взаимная индуктивность). Когда СВЧ импульс имеет резонансную частоту
– их взаимная индуктивность). Когда СВЧ импульс имеет резонансную частоту 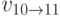 , т.е. соответствующую переходу системы двух кубитов из базисного состояния
, т.е. соответствующую переходу системы двух кубитов из базисного состояния  в базисное состояние
в базисное состояние  , то система кубитов начинает быстро эволюционировать из базисного состояния
, то система кубитов начинает быстро эволюционировать из базисного состояния  в направлении состояния
в направлении состояния  . Вероятность
. Вероятность  считывания состояния
считывания состояния  постепенно уменьшается от 1 до 0, в то время как
постепенно уменьшается от 1 до 0, в то время как 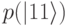 – возрастает от 0 до 1.
После действия
– возрастает от 0 до 1.
После действия  -импульса система находится в смешанном состоянии с волновой функцией
-импульса система находится в смешанном состоянии с волновой функцией 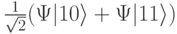 . Из базисного состояния
. Из базисного состояния  в результате взаимодействия с резонансным электромагнитным полем система эволюционирует в направлении состояния
в результате взаимодействия с резонансным электромагнитным полем система эволюционирует в направлении состояния  : после действия
: после действия  -импульса она находится в смешанном состоянии с волновой функцией
-импульса она находится в смешанном состоянии с волновой функцией 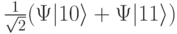 , а после действия
, а после действия  -импульса – уже в состоянии
-импульса – уже в состоянии  .
.
Если СВЧ импульс действует лишь на второй кубит системы, то при начальных базисных состояниях  и
и  система так и остается в начальном состоянии. Если же систему сначала с помощью
система так и остается в начальном состоянии. Если же систему сначала с помощью  -импульса, поданного на первый кубит, перевести в смешанное состояние с волновой функцией
-импульса, поданного на первый кубит, перевести в смешанное состояние с волновой функцией 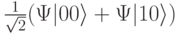 или
или 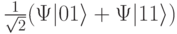 , то после действия на второй кубит
, то после действия на второй кубит  -импульса система переходит в сплетенное состояние с волновой функцией
-импульса система переходит в сплетенное состояние с волновой функцией 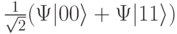 или соответственно – в состояние с волновой функцией
или соответственно – в состояние с волновой функцией 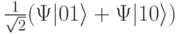 .
Таким образом, оказалось, что систему из двух индуктивно связанных кубитов, действуя на каждый кубит отдельно резонансными СВЧ импульсами, можно использовать как квантовый логический вентиль "Контролируемое отрицание"
.
Таким образом, оказалось, что систему из двух индуктивно связанных кубитов, действуя на каждый кубит отдельно резонансными СВЧ импульсами, можно использовать как квантовый логический вентиль "Контролируемое отрицание"  , который является универсальным квантовым вентилем. Другими словами: над парой индуктивно связанных кубитов с помощью резонансных СВЧ импульсов можно выполнить двухкубитную квантовую логическую операцию
, который является универсальным квантовым вентилем. Другими словами: над парой индуктивно связанных кубитов с помощью резонансных СВЧ импульсов можно выполнить двухкубитную квантовую логическую операцию  .
.
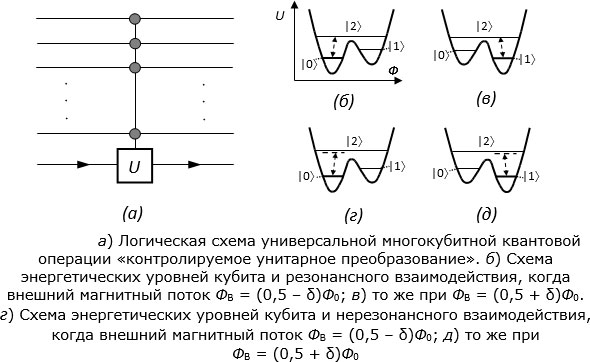
С помощью импульсов СВЧ электромагнитного поля может быть реализована также универсальная многокубитная квантовая логическая операция, которую называют "контролируемое унитарное преобразование" (англ. n-qubit controlled-U gate). Логическая схема такой операции показана на
рис.
10.8.a. Темными кружками здесь условно показаны контролирующие кубиты, а квадратиком с пометкой  – контролируемый кубит, над которым выполняется конкретное однокубитное унитарное преобразование (любое), т.е. поворот вектора состояния этого кубита на сфере Блоха на заданные углы вокруг координатных осей. Это унитарное преобразование реализуется лишь в том случае, если все контролирующие кубиты находятся в базисном состоянии
– контролируемый кубит, над которым выполняется конкретное однокубитное унитарное преобразование (любое), т.е. поворот вектора состояния этого кубита на сфере Блоха на заданные углы вокруг координатных осей. Это унитарное преобразование реализуется лишь в том случае, если все контролирующие кубиты находятся в базисном состоянии 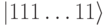 . Если же хотя бы один из них находится в другом состоянии, то унитарное преобразование состояния контролируемого кубита не реализуется.
. Если же хотя бы один из них находится в другом состоянии, то унитарное преобразование состояния контролируемого кубита не реализуется.
Для выполнения указанной многокубитной квантовой логической операции в микроволновом резонаторе ( . "cavity QED"), внутри которого размещены кубиты, возбуждается и поддерживается стоячая СВЧ волна. Все кубиты размещают в ее пучностях. Заметим, что при длине волны порядка 10 мм протяженность "пучности" составляет
. "cavity QED"), внутри которого размещены кубиты, возбуждается и поддерживается стоячая СВЧ волна. Все кубиты размещают в ее пучностях. Заметим, что при длине волны порядка 10 мм протяженность "пучности" составляет 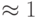 мм. И если "шаг" размещения кубитов будет составлять даже 30 мкм, то в одной "пучности" на площади 1 мм2 вместятся до 1000 миниатюрных кубитов.
мм. И если "шаг" размещения кубитов будет составлять даже 30 мкм, то в одной "пучности" на площади 1 мм2 вместятся до 1000 миниатюрных кубитов.
В этом методе используются не 2, а 3 наиболее низкие энергетические уровня кубита (
рис.
10.8.б): 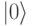 ,
, 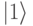 и
и 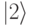 . Эти разрешенные уровни показаны горизонтальными отрезками. Сплошная кривая – это зависимость потенциальной энергии кубита от величины полного магнитного потока сквозь его отверстие. Сокращенно ее называют "потенциальной кривой". Если внешний магнитный поток
. Эти разрешенные уровни показаны горизонтальными отрезками. Сплошная кривая – это зависимость потенциальной энергии кубита от величины полного магнитного потока сквозь его отверстие. Сокращенно ее называют "потенциальной кривой". Если внешний магнитный поток 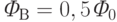 , пронизывающий отверстие кубита, немного уменьшить до
, пронизывающий отверстие кубита, немного уменьшить до  (малая величина
(малая величина 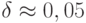 и меньше), то потенциальная кривая кубита становится асимметричной, и энергетический уровень, соответствующий базовому состоянию
и меньше), то потенциальная кривая кубита становится асимметричной, и энергетический уровень, соответствующий базовому состоянию 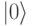 , несколько опускается.
Переход из него на энергетический уровень
, несколько опускается.
Переход из него на энергетический уровень 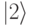 , расположенный выше потенциального барьера между минимумами, становится резонансным со стоячей волной, и кубит за короткое время переходит с уровня
, расположенный выше потенциального барьера между минимумами, становится резонансным со стоячей волной, и кубит за короткое время переходит с уровня 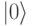 на уровень
на уровень 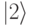 . Если теперь увеличить
. Если теперь увеличить 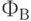 до значения
до значения 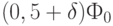 , то асимметрия потенциала меняется на противоположную, ниже становится энергетический уровень, соответствующий базовому состоянию
, то асимметрия потенциала меняется на противоположную, ниже становится энергетический уровень, соответствующий базовому состоянию 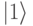 (
рис.
10.8.в), и под действием резонансной стоячей волны кубит переходит с уровня
(
рис.
10.8.в), и под действием резонансной стоячей волны кубит переходит с уровня 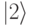 на уровень
на уровень 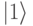 .
.
Оказалось, что взаимодействие возможно не только на резонансных, а и на нерезонансных частотах. Это показано на
рис.
10.8.г и д. Энергии кванта стоячей волны достаточно здесь для возбуждения кубита до уровня, немного ниже, чем энергетический уровень 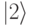 , но расположенного выше потенциального барьера между минимумами.
, но расположенного выше потенциального барьера между минимумами.
По оценке специалистов для реализации  -кубитной квантовой логической операции "контролируемое унитарное преобразование" требуется (
-кубитной квантовой логической операции "контролируемое унитарное преобразование" требуется ( ) "шагов" (в классической вычислительной технике это называют "микрооперациями").
) "шагов" (в классической вычислительной технике это называют "микрооперациями").
Таким образом, для сверхпроводящих кубитов на ПД разработаны не только методы записи и считывания из них квантовой информации, но и эффективные методы реализации над ними функционально полного набора квантовых логических операций.
Работы по оптимизации сверхпроводящих кубитов
За последнее десятилетие выполнен значительный объем теоретических и экспериментальных исследований с целью оптимизации сверхпроводящих кубитов на ПД и схем записи, считывания из них информации, способов выполнения над ними квантовых логических операций. В разных лабораториях мира интенсивно изучали и продолжают изучать, какого типа ПД и с какими параметрами функционируют лучше всего, имеют наименьшую декогерентизацию, оказывают наименьшее влияние на другие элементы квантового процессора. Это потребовало большого объема экспериментальных работ. Мы не станем знакомить вас со всеми деталями таких исследований, однако считаем нужным дать вам общее представление о сути этой кропотливой работы.
Для того, чтобы детально разобраться в механизмах квантовых вычислений и оптимизировать их ход, очень важной является томография квантового состояния кубитов, о которой мы уже рассказывали в "Квантовые процессоры на основе спинового магнитного резонанса" . Она особенно сложна в тех случаях, когда квантовое состояние кубита является гибридным, т.е. "смесью" его базовых состояний. Напомним, что за одну серию измерений можно определить проекцию вектора Блоха лишь на одну из координатных осей. Чтобы определить все три проекции и детальнее знать квантовое состояние кубита, надо проводить несколько серий измерений. Еще сложнее разбираться в "сплетенных" состояниях нескольких кубитов.
На сегодняшний день относительно разных видов сверхпроводящих кубитов предложены и детально рассмотрены все томографические процедуры, необходимые для определения квантового состояния как отдельного кубита, так и пары взаимосвязанных сверхпроводящих кубитов и даже ансамбля из многих кубитов. Особенно ценным оказалось то, что предложенные процедуры томографических измерений для ансамблей из многих сверхпроводящих кубитов удается проводить в пределах короткого времени порядка 5-20 нс. Это ведь очень важно в случаях, когда время сохранения когерентности мало.
Теоретически и экспериментально исследуются зависимости характеристик функционирования кубитов и групп кубитов от всех конструктивных и технологических параметров: от размеров и формы элементов кубитов и от их взаимного расположения, от физической структуры переходов Джозефсона, от материалов, из которых они изготовлены, от деталей технологии изготовления и т.п. Например, для фазовых кубитов на ПД было установлено, что из разных возможных материалов сверхпроводника наибольшее время сохранения когерентности обеспечивают сверхпроводники из алюминия. Показано, что потоковые кубиты на ПД со структурой SNS (сверхпроводник – нормальный металл – сверхпроводник) работают быстрее, чем со структурой SIS (сверхпроводник – изолятор – сверхпроводник).
Оказалось, что значительно улучшить работу сверхпроводящих кубитов помогает шунтирование ПД дополнительными элементами. Разработана теоретическая модель, описывающая функционирование ПД с шунтами. Показано, что шунтирование ПД типа SIS в сверхпроводящих потоковых кубитах нелинейными переходами типа SIN (сверхпроводник –изолятор – нормальный металл) изменяет динамику кубита в лучшую сторону. В частности, значительно уменьшаются дробовой шум электрического тока, электромагнитное влияние на соседние кубиты, демпфируются колебания, возникающие обычно при выполнении логических операций над кубитами и при считывании их состояния. Экспериментально исследуются шунты с разной структурой (например,  и другие).
и другие).
Теоретически и экспериментально исследуются структуры "кубит + считывающий сквид". Показано, что оптимальное шунтирование переходов Джозефсона во внешнем считывающем сквиде, значительно уменьшает влияние измерительного сквида на кубит и содействует удлинению состояния когерентности последнего на порядок – вплоть до значений около 200 мкс. Оптимальным признано чисто емкостное шунтирование каждого из двух симметричных ПД. Чувствительность считывания определяется при этом в основном квантовым шумом усилителя.
Выполнен теоретический анализ компаратора для быстрого (~10 пс) считывания состояния кубита на ПД с учетом реального индуктивного импеданса кубитов и флуктуаций от неконтролируемых внешних влияний (в первую очередь магнитных). Предложена квантовая схема с использованием компенсирующей обратной связи для уменьшения таких внешних влияний. Разработан экспериментальный сверхпроводящий компаратор, обеспечивающий быстрое (за 30-50 пс) считывание информации со сверхпроводящих кубитов, необходимое для реализации схем коррекции сбоев при квантовых вычислениях.
Вся эта коллективная работа значительно продвинула вперед всю технологию изготовления и использования сверхпроводящих кубитов на переходах Джозефсона, сделала эти кубиты одним из самых перспективных направлений реализации квантовых процессоров.