|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Квантовые процессоры на переходах Джозефсона
Потоковые кубиты
Преодолеть недостатки зарядовых кубитов можно, если устранить кулоновское взаимодействие электрических зарядов, т.е. сделать так, чтобы в обоих базовых состояниях кубита 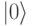 и
и 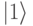 суммарный электрический заряд кубита равнялся нулю. Это условие выполняется в т.н. "потоковых" кубитах (англ. flux qubit), которые строят на сквидах с одним или с несколькими ПД. Площадь ПД здесь должна быть значительно больше, чем в зарядовых кубитах, чтобы выполнялось условие
суммарный электрический заряд кубита равнялся нулю. Это условие выполняется в т.н. "потоковых" кубитах (англ. flux qubit), которые строят на сквидах с одним или с несколькими ПД. Площадь ПД здесь должна быть значительно больше, чем в зарядовых кубитах, чтобы выполнялось условие  . Принцип действия потокового кубита с одним ПД объясним с помощью
рис.
10.3.
. Принцип действия потокового кубита с одним ПД объясним с помощью
рис.
10.3.
Здесь условно показан замкнутый сверхпроводящий контур с одним ПД, отверстие которого пронизывает внешний магнитный поток  . Благодаря макроскопической квантовой интерференции в контуре устанавливается такой сверхпроводящий ток
. Благодаря макроскопической квантовой интерференции в контуре устанавливается такой сверхпроводящий ток 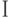 , чтобы суммарный магнитный поток
, чтобы суммарный магнитный поток  через контур был кратным кванту магнитного потока
через контур был кратным кванту магнитного потока  (лекция 3, формула (3.1)). Для этого магнитный поток, обусловленный сверхпроводящим током
(лекция 3, формула (3.1)). Для этого магнитный поток, обусловленный сверхпроводящим током 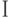 , уменьшает или увеличивает
, уменьшает или увеличивает  на соответствующую величину.
Поэтому сверхпроводящий контур может находиться в двух базовых состояниях:
на соответствующую величину.
Поэтому сверхпроводящий контур может находиться в двух базовых состояниях: 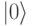 , когда ток течет в нем по часовой стрелке или
, когда ток течет в нем по часовой стрелке или 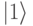 , – когда против часовой стрелки. На ПД автоматически устанавливается нужная разность фаз
, – когда против часовой стрелки. На ПД автоматически устанавливается нужная разность фаз  – в соответствии с приведенной в лекции 3 формулой (3.4).
– в соответствии с приведенной в лекции 3 формулой (3.4).
Внешний магнитный поток  называют еще "потоком смещения", так как он влияет на характер зависимости потенциальной энергии кубита от суммарного магнитного потока
называют еще "потоком смещения", так как он влияет на характер зависимости потенциальной энергии кубита от суммарного магнитного потока  сквозь отверстие его сверхпроводящего контура и, следовательно, на расположение разрешенных энергетических уровней. На
рис.
10.4 эти зависимости показаны для двух типичных случаев, когда (а) поток смещения равен точно половине
сквозь отверстие его сверхпроводящего контура и, следовательно, на расположение разрешенных энергетических уровней. На
рис.
10.4 эти зависимости показаны для двух типичных случаев, когда (а) поток смещения равен точно половине  , и (б) когда значение
, и (б) когда значение  отличается от
отличается от  .
.
В обоих случаях потоковый кубит имеет 2 потенциальных минимума. Но в случае (а) потенциал кубита является симметричным, а в случае (б) симметрия исчезает. И соответственно расходятся энергетические уровни базовых состояний кубита. Благодаря этому появляется возможность манипулировать квантовым состоянием потокового кубита с помощью импульсов высокочастотного электромагнитного поля, как это будет описано ниже.
В кубитах с несколькими ПД квантование магнитного потока сквозь отверстие сверхпроводящего контура приводит к установлению следующего соотношения между фазами на всех ПД:
 |
( 10.6) |
 – перепад фазы на
– перепад фазы на 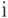 -м ПД, а
-м ПД, а  – фаза, пропорциональная величине внешнего магнитного потока сквозь контур.
– фаза, пропорциональная величине внешнего магнитного потока сквозь контур.Применение нескольких ПД в сверхпроводящем контуре позволяет значительно уменьшить геометрические размеры контура. А это одновременно уменьшает и влияние на кубит неконтролируемых флуктуаций случайных внешних магнитных и электромагнитных полей и этим способствует сохранению когерентности кубитов.
В лекции 3 были описаны очень чувствительные магнитометры постоянного тока на сквидах с двумя ПД. В квантовых процессорах их применяют для считывания состояния сверхпроводящих потоковых кубитов.
Один из наиболее исследованных вариантов потокового кубита с двумя ПД показан на рис. 10.5. Слева приведена его принципиальная схема.
Базовые состояния этого кубита определяются малым сверхпроводящим контуром 1 с двумя одинаковыми ПД. Внешний сверхпроводящий контур 2 с ПД большей площади (и соответственно с большим критическим током) обеспечивает возможность юстировки схемы, считывания и "записи" нужного базового состояния кубита. Изменяя магнитный поток  , можно влиять на глубину потенциальных минимумов.
, можно влиять на глубину потенциальных минимумов.
Справа показано, что при  можно точно уравнять глубину потенциальных минимумов (кривая 5), а немного изменяя этот магнитный поток, можно нарушить симметрию в ту или другую сторону (кривая 6) и тем самым заставить кубит перейти в заданное начальное базовое состояние. Изменяя магнитный поток
можно точно уравнять глубину потенциальных минимумов (кривая 5), а немного изменяя этот магнитный поток, можно нарушить симметрию в ту или другую сторону (кривая 6) и тем самым заставить кубит перейти в заданное начальное базовое состояние. Изменяя магнитный поток  , можно влиять на высоту потенциального барьера между двумя минимумами (кривые 7 и 8), регулируя устойчивость кубита и его чувствительность к внешним воздействиям.
, можно влиять на высоту потенциального барьера между двумя минимумами (кривые 7 и 8), регулируя устойчивость кубита и его чувствительность к внешним воздействиям.
Вместо внешнего магнитного потока в "большой" сверхпроводящий контур 2 можно подать электрический ток смещения. Управление кубитом при необходимости можно также осуществлять дистанционно – с помощью сверхпроводящего трансформатора магнитного потока 3 и дополнительного сквида постоянного тока 4.
В описанном варианте потоковый кубит значительно лучше поддается изучению, регулированию и управлению, чем потоковый кубит с одним ПД ( рис. 10.3). В то же время и "лазеек" для декогерентизации становится в нем больше, и их надо тщательнее "закрывать".
Фазовые кубиты
Слева на
рис.
10.6 показана принципиальная схема кубита 1 с тремя ПД. В его сверхпроводящий контур входят два одинаковые ПД (ПД1 и ПД2) и третий (ПД3), имеющий намного меньшую площадь и поэтому большую зарядовую энергию  и меньшую джозефсоновскую энергию
и меньшую джозефсоновскую энергию  .
.

Рис. 10.6. Слева – схема кубита 1 с тремя ПД, расположенного внутри сквида постоянного тока 2. Справа – микрофотография одного из образцов такой структуры
Такие кубиты имеют уже две "степени свободы" – независимые перепады фазы на двух одинаковых ПД. Поэтому их называют "фазовыми". Зависимость потенциальной энергии фазового кубита от суммарного магнитного потока  сквозь его отверстие имеет форму периодической двумерной поверхности с потенциальными минимумами. Качественно состояния кубита с тремя ПД подобны кубиту с одним ПД, но количественные параметры существенно отличаются, и, используя дополнительную степень свободы, эксплуатационные параметры кубита удается значительно улучшить.
сквозь его отверстие имеет форму периодической двумерной поверхности с потенциальными минимумами. Качественно состояния кубита с тремя ПД подобны кубиту с одним ПД, но количественные параметры существенно отличаются, и, используя дополнительную степень свободы, эксплуатационные параметры кубита удается значительно улучшить.
В одной из особенно удачных модификаций фазового кубита с тремя ПД средний переход имеет структуру "сверхпроводник-ферромагнетик-сверхпроводник" (S-F-S). Сверхпроводящий ток через такой переход стабилен лишь тогда, когда сдвиг фаз на этом ПД составляет  . Поэтому такой, более стабильный, кубит называют
. Поэтому такой, более стабильный, кубит называют  -кубитом. При отсутствии внешнего магнитного поля он имеет два основных квантовых состояния, манипулировать которыми позволяет уже очень слабый магнитный поток порядка
-кубитом. При отсутствии внешнего магнитного поля он имеет два основных квантовых состояния, манипулировать которыми позволяет уже очень слабый магнитный поток порядка  .
.
Расстояние между энергетическими уровнями двух базовых состояний фазового кубита очень мало, и поэтому такой кубит может надежно функционировать лишь при температурах ниже 20 мК. Вместе с тем он может иметь нанометровые размеры и совсем небольшой ток сверхпроводимости (~10 нА), что способствует достижению высокого уровня интеграции.
Фазовый кубит 1 обычно размещают внутри сквида постоянного тока (2). Магнитный поток, пронизывающий отверстие кубита, в такой конструкции одновременно пронизывает и отверстие сквида 2, что позволяет легко измерять состояние кубита после разнообразных манипуляций с ним. Справа приведена микрофотография внешнего вида одного из образцов такого кубита.



