|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Квантовые процессоры на основе спинового магнитного резонанса
Ансамблевый ЯМР квантовый процессор
Сигналы от одноэлектронных транзисторов при считывании конечного состояния кубитов оказались слабыми, что предопределяет значительные погрешности считывания. Чтобы повысить надежность считывания, была предложена идея "ансамблевого" ЯМР квантового процессора. Она заключается в том, что на пластине бесспинового кремния создается не один ряд, а много параллельных рядов спиновых кубитов – целый "ансамбль" квантовых регистров. Принцип их расположения иллюстрирует рис. 9.8.
Здесь в проекции сверху показан один из участков пластины кремния, на котором видно 5 строк атомов  по 8 атомов в каждой строке. На самом деле каждая строка довольно длинная и может состоять из 1-2 тысяч кубитов. Это – отдельный квантовый регистр. Строк тоже может быть не 5, а много тысяч. Образованные ими квантовые регистры функционируют параллельно, одинаково и независимо друг от друга. Для управления их работой, как и в варианте Б. Кейна, используют металлические электроды A и B, проложенные над одноименными кубитами сквозь весь массив. На
рис.
9.8 они показаны в виде заштрихованных полосок.
Если, например, в ансамбле используется 10 тысяч строк, расположенных с периодом 30 нм, то на пластине кремния они занимают область шириной 0,3 мм, т.е. легко размещаются между полюсами пары катушек, с помощью которых создается поперечное магнитное поле. Большое количество параллельно функционирующих квантовых регистров значительно облегчает задачу считывания их конечного состояния. Ведь в одинаковом конечном состоянии оказываются сразу тысячи одноименных кубитов. И их состояние становится возможным измерять с помощью хорошо отработанных методов.
по 8 атомов в каждой строке. На самом деле каждая строка довольно длинная и может состоять из 1-2 тысяч кубитов. Это – отдельный квантовый регистр. Строк тоже может быть не 5, а много тысяч. Образованные ими квантовые регистры функционируют параллельно, одинаково и независимо друг от друга. Для управления их работой, как и в варианте Б. Кейна, используют металлические электроды A и B, проложенные над одноименными кубитами сквозь весь массив. На
рис.
9.8 они показаны в виде заштрихованных полосок.
Если, например, в ансамбле используется 10 тысяч строк, расположенных с периодом 30 нм, то на пластине кремния они занимают область шириной 0,3 мм, т.е. легко размещаются между полюсами пары катушек, с помощью которых создается поперечное магнитное поле. Большое количество параллельно функционирующих квантовых регистров значительно облегчает задачу считывания их конечного состояния. Ведь в одинаковом конечном состоянии оказываются сразу тысячи одноименных кубитов. И их состояние становится возможным измерять с помощью хорошо отработанных методов.
Параллельная работа целого ансамбля одинаковых квантовых регистров позволяет также, благодаря усреднению, уменьшить влияние многих технологических неточностей, например, некоторых незначительных технологических отклонений в расположении атомов  , в ширине управляющих электродов и т.п.
, в ширине управляющих электродов и т.п.
Тем не менее, управляющие потенциалы и радиоимпульсы резонансного магнитного поля, с помощью которых выполняются квантовые логические операции над кубитами, остаются общими и одинаково влияют на все аналогичные кубиты. Эти незначительные отклонения приводят к накоплению одинаковых ошибок. И параллельная работа тысяч квантовых регистров не уменьшает влияние декогерентизации.
ЯМР квантовый процессор на основе атомов, капсулированных в фуллеренах
В 2011 г. [Ju C., Suter D., Du J. An endohedral fullerene-based nuclear spin quantum computer. // Physics Letters A. – 2009. – V. 375. – P. 1441–1444] был предложен другой вариант ЯМР квантового процессора, в котором в качестве кубитов используются атомы со спином ядра 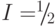 , капсулированные внутри фуллерена. Такими кубитами могут быть, например, атомы изотопов азота
, капсулированные внутри фуллерена. Такими кубитами могут быть, например, атомы изотопов азота 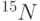 или фосфора
или фосфора  , капсулированные внутри фуллерена
, капсулированные внутри фуллерена  . Изолированные углеродной оболочкой от окружения, эти атомы не являются химически связанными, а являются в достаточной мере "свободными". У самой молекулы
. Изолированные углеродной оболочкой от окружения, эти атомы не являются химически связанными, а являются в достаточной мере "свободными". У самой молекулы  суммарный ядерный и суммарный электронный спин равны нулю, и поэтому молекула фуллерена не реагирует на внешнее магнитное поле.
суммарный ядерный и суммарный электронный спин равны нулю, и поэтому молекула фуллерена не реагирует на внешнее магнитное поле.
Атомы  и
и  могут иметь лишь два значения ядерного магнитного квантового числа:
могут иметь лишь два значения ядерного магнитного квантового числа:  . А суммарный электронный спин у каждого из названных "свободных" атомов
. А суммарный электронный спин у каждого из названных "свободных" атомов  . И поэтому магнитное квантовое число электронной оболочки такого атома может принимать 4 разных значения
. И поэтому магнитное квантовое число электронной оболочки такого атома может принимать 4 разных значения  .
.
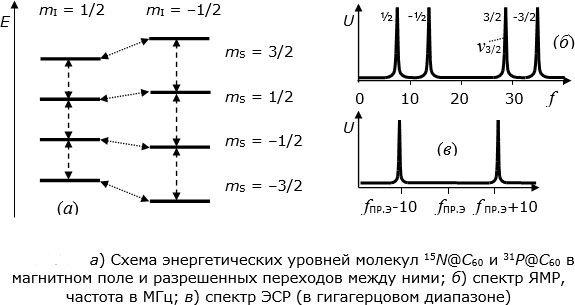
Во внешнем магнитном поле основной энергетический уровень капсулированного внутри фуллерена атома расщепляется на 8 разрешенных энергетических уровней, как показано на
рис.
9.9.а. Штриховыми стрелками показаны разрешенные ( ) электронные переходы между этими энергетическими уровнями, а пунктирными стрелками – разрешенные ядерные переходы (
) электронные переходы между этими энергетическими уровнями, а пунктирными стрелками – разрешенные ядерные переходы ( ).
).
Во внешнем магнитном поле с индукцией 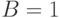 Тл резонансная частота
Тл резонансная частота  прецессии магнитного момента электронов составляет приблизительно 28 ГГц. Резонансная частота
прецессии магнитного момента электронов составляет приблизительно 28 ГГц. Резонансная частота  прецессии магнитного момента ядра существенно зависит от ориентации магнитного момента электронов, т.е. от значения магнитного квантового числа
прецессии магнитного момента ядра существенно зависит от ориентации магнитного момента электронов, т.е. от значения магнитного квантового числа  .
.
Спектр ядерного магнитного резонанса для  в магнитном поле с индукцией
в магнитном поле с индукцией 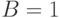 Тл показан на
рис.
9.9.б. Вдоль горизонтали отложена частота в мегагерцах. Как видим, ЯМР наблюдается в радиочастотной области спектра. В спектре ЯМР присутствуют 4 резонансных пика, соответствующих разрешенным ядерным переходам, обозначенным на
рис.
9.9.а пунктирными стрелками. Частота, при которой наблюдается каждый пик, является частотой прецессии магнитного момента ядра при соответствующем значении квантового числа
Тл показан на
рис.
9.9.б. Вдоль горизонтали отложена частота в мегагерцах. Как видим, ЯМР наблюдается в радиочастотной области спектра. В спектре ЯМР присутствуют 4 резонансных пика, соответствующих разрешенным ядерным переходам, обозначенным на
рис.
9.9.а пунктирными стрелками. Частота, при которой наблюдается каждый пик, является частотой прецессии магнитного момента ядра при соответствующем значении квантового числа  , которое написано рядом с пиком.
, которое написано рядом с пиком.
Спектр электронного спинового резонанса (ЕСР), показанный на
рис.
9.9.в, наблюдается в микроволновой области спектра вблизи частоты  ГГц. В нем наблюдаются лишь 2 резонансных пика, соответствующих разрешенным электронным переходам, обозначенным на
рис.
9.9.а штриховыми стрелками. Расстояние между ними порядка 20 МГц очень мало по сравнению с
ГГц. В нем наблюдаются лишь 2 резонансных пика, соответствующих разрешенным электронным переходам, обозначенным на
рис.
9.9.а штриховыми стрелками. Расстояние между ними порядка 20 МГц очень мало по сравнению с  . Левый пик наблюдается, когда магнитный момент ядра находится в состоянии
. Левый пик наблюдается, когда магнитный момент ядра находится в состоянии  (ориентирован в направлении магнитного поля), правый – в состоянии
(ориентирован в направлении магнитного поля), правый – в состоянии  (ориентирован навстречу магнитному полю).
(ориентирован навстречу магнитному полю).
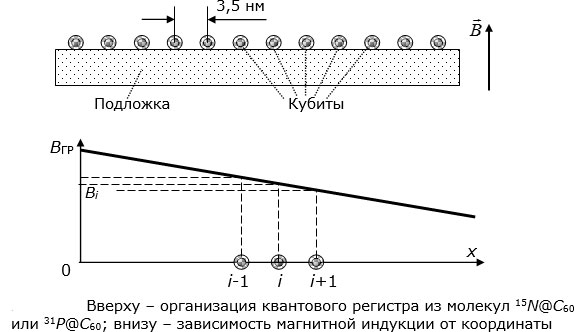
Квантовый регистр состоит из цепи молекул  или
или  , иммобилизованных на диэлектрической подложке и выстроенных в одну линию с периодом расположения 3,5 нм (
рис.
9.10, вверху). Внешнее постоянное однородное магнитное поле ориентировано вдоль вертикали.
, иммобилизованных на диэлектрической подложке и выстроенных в одну линию с периодом расположения 3,5 нм (
рис.
9.10, вверху). Внешнее постоянное однородное магнитное поле ориентировано вдоль вертикали.
Кроме однородного, создается также постоянное градиентное магнитное поле  . Характер зависимости магнитной индукции в нем от координаты показан на
рис.
9.10 внизу. На каждый кубит действует свое по величине дополнительное магнитное поле. И согласно формуле (10.3) каждый кубит имеет свою частоту электронного спинового резонанса. Величина градиента магнитного поля подобрана так, чтобы резонансные частоты соседних кубитов отличались на величину (порядка 40 МГц), достаточную для того, чтобы состоянием каждого кубита можно было манипулировать независимо.
. Характер зависимости магнитной индукции в нем от координаты показан на
рис.
9.10 внизу. На каждый кубит действует свое по величине дополнительное магнитное поле. И согласно формуле (10.3) каждый кубит имеет свою частоту электронного спинового резонанса. Величина градиента магнитного поля подобрана так, чтобы резонансные частоты соседних кубитов отличались на величину (порядка 40 МГц), достаточную для того, чтобы состоянием каждого кубита можно было манипулировать независимо.
Квантовое состояние каждого кубита определяется пространственной ориентацией магнитного момента ядра. За базовое состояние 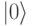 принимается ориентация в направлении магнитного поля (
принимается ориентация в направлении магнитного поля ( ), а за базовое состояние
), а за базовое состояние 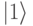 – ориентация против направления магнитного поля (
– ориентация против направления магнитного поля ( ). Кроме квантового состояния различают еще 2 режима работы кубитов – пассивный и активный. Пассивным называют режим, когда
). Кроме квантового состояния различают еще 2 режима работы кубитов – пассивный и активный. Пассивным называют режим, когда  , активным – когда
, активным – когда  . Они существенно отличаются по частоте ЯМР (см.
рис.
9.9.б). При низких температурах обычно
. Они существенно отличаются по частоте ЯМР (см.
рис.
9.9.б). При низких температурах обычно  , и все кубиты находятся в пассивном режиме.
, и все кубиты находятся в пассивном режиме.
Если надо выполнить однокубитную квантовую логическую операцию над 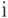 -м кубитом, то сначала этот кубит переводят в активный режим. Для этого используют микроволновый
-м кубитом, то сначала этот кубит переводят в активный режим. Для этого используют микроволновый  -импульс на частоте
-импульс на частоте  , которая соответствует значению магнитного поля
, которая соответствует значению магнитного поля  в точке расположения этого кубита. Другие кубиты на этот импульс не откликаются, так как имеют другую резонансную частоту ЭСР. После действия этого микроволнового импульса электронный спин поворачивается на угол
в точке расположения этого кубита. Другие кубиты на этот импульс не откликаются, так как имеют другую резонансную частоту ЭСР. После действия этого микроволнового импульса электронный спин поворачивается на угол  , и значение
, и значение  изменяется с (–3/2) на (+3/2). Время надежного пребывания электронного спина в таком состоянии уже при температуре 5 К превышает 1 с, а при более низких температурах становится еще более длительным.
В активном режиме с помощью импульсов поперечного магнитного поля на частоте
изменяется с (–3/2) на (+3/2). Время надежного пребывания электронного спина в таком состоянии уже при температуре 5 К превышает 1 с, а при более низких температурах становится еще более длительным.
В активном режиме с помощью импульсов поперечного магнитного поля на частоте 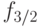 (
рис.
9.9.б) можно выполнить любые квантовые логические операции над магнитным моментом ядра, как было описано в предыдущих подразделах. Другие кубиты на такие радиоимпульсы не реагируют, так как находятся в пассивном режиме и имеют существенно другую резонансную частоту. После завершения квантовых логических операций над магнитным моментом ядра с помощью еще одного микроволнового
(
рис.
9.9.б) можно выполнить любые квантовые логические операции над магнитным моментом ядра, как было описано в предыдущих подразделах. Другие кубиты на такие радиоимпульсы не реагируют, так как находятся в пассивном режиме и имеют существенно другую резонансную частоту. После завершения квантовых логических операций над магнитным моментом ядра с помощью еще одного микроволнового  -импульса электронный спин еще раз поворачивают на угол
-импульса электронный спин еще раз поворачивают на угол  , и значение
, и значение  изменяется с (+3/2) на (–3/2), благодаря чему кубит возвращается в пассивный режим. Дальше таким же образом можно выполнять квантовые логические операции над следующим кубитом.
изменяется с (+3/2) на (–3/2), благодаря чему кубит возвращается в пассивный режим. Дальше таким же образом можно выполнять квантовые логические операции над следующим кубитом.
Для выполнения двухкубитных квантовых логических операций используют взаимодействие электронных магнитных моментов соседних кубитов. Именно для этого и было выбрано столь малое расстояние между кубитами (3,5 нм). Детальный механизм выполнения таких операций является многостадийным и довольно громоздким. Поэтому описывать его во всех деталях мы не будем. Раскроем лишь его физическую суть. Она заключается в том, что сначала первый кубит переводится в активный режим. Квантовое состояние  магнитного момента его ядра передается в состояние
магнитного момента его ядра передается в состояние  его электронного магнитного момента. Затем и второй кубит переводится в активный режим. В результате взаимодействия электронных магнитных моментов квантовое состояние
его электронного магнитного момента. Затем и второй кубит переводится в активный режим. В результате взаимодействия электронных магнитных моментов квантовое состояние  передается на квантовое состояние
передается на квантовое состояние  электронного магнитного момента второго кубита.
Далее с помощью соответствующих радиочастотных и микроволновых импульсов выполняется требуемая двухкубитная логическая операция над квантовыми состояниями
электронного магнитного момента второго кубита.
Далее с помощью соответствующих радиочастотных и микроволновых импульсов выполняется требуемая двухкубитная логическая операция над квантовыми состояниями  и
и  (это – квантовое состояние ядерного магнитного момента 2-го кубита). Образующееся в результате квантовое состояние
(это – квантовое состояние ядерного магнитного момента 2-го кубита). Образующееся в результате квантовое состояние  передается в квантовое состояние
передается в квантовое состояние  , а из него – в квантовое состояние
, а из него – в квантовое состояние  . И в завершение оба кубита возвращаются в пассивный режим. Разработаны детальные последовательности манипуляций, требуемых для выполнения всех основных двухкубитных квантовых логических операций. Разрабатываются последовательности манипуляций, требуемых для выполнения некоторых трехкубитных и многокубитных квантовых логических операций.
. И в завершение оба кубита возвращаются в пассивный режим. Разработаны детальные последовательности манипуляций, требуемых для выполнения всех основных двухкубитных квантовых логических операций. Разрабатываются последовательности манипуляций, требуемых для выполнения некоторых трехкубитных и многокубитных квантовых логических операций.
Несомненными преимуществами этого варианта ЯМР квантового процессора являются его "молекулярно малые" размеры и то, что здесь удалось обойтись совсем без управляющих электродов. Ядерные магнитные моменты хорошо изолированы молекулами фуллерена от многих посторонних влияний. Однако за отсутствие электродов здесь приходится расплачиваться заметным увеличением числа манипуляций (микроопераций, т.е. микроволновых и радиоимпульсов), требуемых для выполнения квантовых логических операций. А это приводит к более быстрому накоплению отклонений в состоянии кубитов, обусловленных неточностью выполнения отдельных манипуляций, т.е. к росту скорости декогерентизации. Пока еще не решенной в этом варианте проблемой остается и считывание конечного состояния кубитов – из-за их малости и близости друг к другу.