|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Квантовые процессоры на основе спинового магнитного резонанса
Возможности манипулирования состоянием спинового кубита с помощью резонансного поперечного магнитного поля
Кроме постоянного магнитного поля  , которое считается продольным, на спиновый кубит можно подействовать переменным поперечным магнитным полем
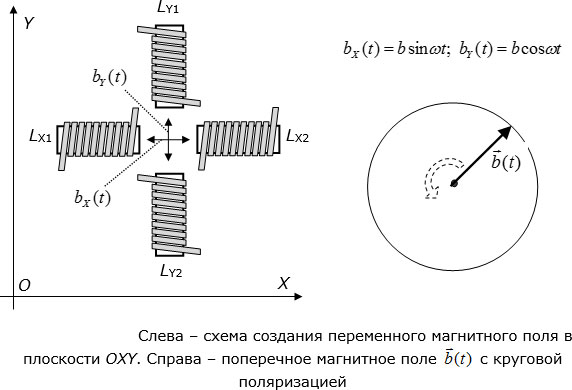
, которое считается продольным, на спиновый кубит можно подействовать переменным поперечным магнитным полем 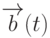 . В некоторых методиках ядерного магнитного резонанса (ЯМР) для создания такого переменного поперечного магнитного поля используют 2 пары катушек с ортогональными осями. Такие катушки показаны на
рис.
9.3 слева, там же показана и система координат
. В некоторых методиках ядерного магнитного резонанса (ЯМР) для создания такого переменного поперечного магнитного поля используют 2 пары катушек с ортогональными осями. Такие катушки показаны на
рис.
9.3 слева, там же показана и система координат  .
.
Если сквозь обмотки катушек 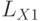 и
и 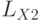 пропускать переменный электрический ток с частотой
пропускать переменный электрический ток с частотой  , то в зазоре между сердечниками этих катушек создается переменное магнитное поле
, то в зазоре между сердечниками этих катушек создается переменное магнитное поле 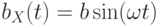 такой же частоты, ориентированное вдоль оси
такой же частоты, ориентированное вдоль оси 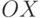 . Если пропускать переменный электрический ток с частотой
. Если пропускать переменный электрический ток с частотой  сквозь обмотки катушек
сквозь обмотки катушек 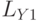 и
и 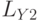 , то в зазоре между их сердечниками создается переменное магнитное поле
, то в зазоре между их сердечниками создается переменное магнитное поле 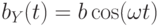 такой же частоты, ориентированное вдоль оси
такой же частоты, ориентированное вдоль оси  . Если частоты и амплитуды магнитных полей
. Если частоты и амплитуды магнитных полей  и
и 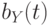 одинаковы, а сдвиг фаз между ними равен
одинаковы, а сдвиг фаз между ними равен  , то в сумме они образуют магнитное поле
, то в сумме они образуют магнитное поле 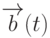 с круговой поляризацией (
рис.
9.3 справа).
Вектор магнитной индукции
с круговой поляризацией (
рис.
9.3 справа).
Вектор магнитной индукции  равномерно вращается в плоскости
равномерно вращается в плоскости 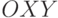 с угловой скоростью
с угловой скоростью  , оставаясь все время ортогональным к вектору
, оставаясь все время ортогональным к вектору  постоянного магнитного поля кубита, который направлен вдоль оси
постоянного магнитного поля кубита, который направлен вдоль оси 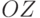 . В случае резонанса, когда угловая частота
. В случае резонанса, когда угловая частота  поперечного магнитного поля с круговой поляризацией точно равняется угловой частоте ларморовой прецессии
поперечного магнитного поля с круговой поляризацией точно равняется угловой частоте ларморовой прецессии 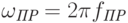 , вектор магнитной индукции
, вектор магнитной индукции  вращается с такой же частотой, как и магнитный момент
вращается с такой же частотой, как и магнитный момент  кубита.
кубита.
Поэтому в ПСК, вращающейся с угловой скоростью 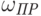 вокруг оси
вокруг оси  , вектор магнитной индукции
, вектор магнитной индукции  неподвижен. Из-за этого в ПСК вокруг вектора
неподвижен. Из-за этого в ПСК вокруг вектора  тоже начинается дополнительная прецессия магнитного момента
тоже начинается дополнительная прецессия магнитного момента  с частотой
с частотой
 |
( 9.5) |
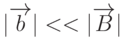 , и поэтому частота Раби
, и поэтому частота Раби 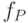 намного меньше частоты ларморовой прецессии
намного меньше частоты ларморовой прецессии  . Эту дополнительную прецессию мы назовем "прецессией Раби".
. Эту дополнительную прецессию мы назовем "прецессией Раби".На
рис.
9.4 слева показан случай, когда момент включения радиочастотного импульса (относительно фазы ларморовой прецессии) выбран так, чтобы в ПСК вектор магнитной индукции  был направлен перпендикулярно к вектору Блоха ОМ и к его проекции ON на координатную плоскость OXY.
был направлен перпендикулярно к вектору Блоха ОМ и к его проекции ON на координатную плоскость OXY.
Направление ОМ совпадает с направлением магнитного момента  . Поскольку вектор ОМ перпендикулярен к
. Поскольку вектор ОМ перпендикулярен к  , то прецессия Раби в данном случае происходит так, что конец М перемещается вдоль большого круга DMED, выделенного штриховой линией. Поэтому изменяется лишь угол
, то прецессия Раби в данном случае происходит так, что конец М перемещается вдоль большого круга DMED, выделенного штриховой линией. Поэтому изменяется лишь угол  , азимутальный угол
, азимутальный угол 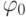 остается в ПСК неизменным.
остается в ПСК неизменным.
Если длительность импульса резонансного поперечного магнитного поля 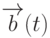
 |
( 9.6) |
 спинового кубита повернется вокруг вектора магнитной индукции
спинового кубита повернется вокруг вектора магнитной индукции  точно на угол
точно на угол  . В технике ЯМР такой резонансный радиочастотный импульс называют пи-импульсом (
. В технике ЯМР такой резонансный радиочастотный импульс называют пи-импульсом ( -импульсом или
-импульсом или 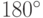 импульсом). Аналогично резонансные радиочастотные импульсы с длительностью, которая обеспечивает поворот магнитного момента
импульсом). Аналогично резонансные радиочастотные импульсы с длительностью, которая обеспечивает поворот магнитного момента  точно на углы
точно на углы 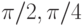 и т.п., называют соответственно
и т.п., называют соответственно  -импульсом (90?-импульсом),
-импульсом (90?-импульсом), 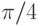 -импульсом (
-импульсом (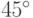 -импульсом) и т.д.
-импульсом) и т.д.На
рис.
9.4 справа показан другой случай, когда радиочастотный импульс включается в такой момент времени, когда направление вектора  совпадает с направлением оси OY в ПСК. В этом случае прецессия Раби магнитного момента
совпадает с направлением оси OY в ПСК. В этом случае прецессия Раби магнитного момента  в ПСК происходит так, что конец вектора перемещается вдоль малого круга ABCFA, выделенного штриховой линией. В ходе такой прецессии одновременно изменяются оба угла
в ПСК происходит так, что конец вектора перемещается вдоль малого круга ABCFA, выделенного штриховой линией. В ходе такой прецессии одновременно изменяются оба угла  . Регулируя длительность радиочастотного импульса, можно согласованно изменить эти углы в пределах окружности ABCF.
. Регулируя длительность радиочастотного импульса, можно согласованно изменить эти углы в пределах окружности ABCF.
Таким образом, квантово-механический анализ показывает, что, выбирая момент включения и продолжительность импульса резонансного поперечного магнитного поля 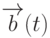 , можно довольно точно манипулировать ориентацией магнитного момента
, можно довольно точно манипулировать ориентацией магнитного момента  , и, следовательно, состоянием спинового кубита.
, и, следовательно, состоянием спинового кубита.
Если возвратиться к квантовым логическим операциям над кубитом (
"Квантовые процессоры на основе спинового магнитного резонанса"
), то оказывается, что, точно подбирая моменты включения и продолжительность радиоимпульсов резонансного поперечного магнитного поля 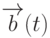 , можно обеспечить поворот вектора Блоха на заданную величину в любом направлении, т.е. выполнить над спиновым кубитом любую заданную квантовую логическую операцию.
, можно обеспечить поворот вектора Блоха на заданную величину в любом направлении, т.е. выполнить над спиновым кубитом любую заданную квантовую логическую операцию.
Легко понять, что в случае, изображенном на
рис.
9.4 слева,  -импульс приводит к инверсии квантового состояния спинового кубита, т.е. выполняет над ним квантовую логическую операцию отрицания.
-импульс приводит к инверсии квантового состояния спинового кубита, т.е. выполняет над ним квантовую логическую операцию отрицания.
Если спиновый кубит находился в базовом состоянии 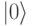 , то
, то  -импульс переведет его в смешанное состояние, которое описывается волновой функцией
-импульс переведет его в смешанное состояние, которое описывается волновой функцией ![\frac{\sqrt{2}}{2}[\Psi(|1\rangle)+\Psi(|0\rangle)]](/sites/default/files/tex_cache/965184f16a8cf2cc37855082a258a2ab.png) .
.
Уже найдены и хорошо отработаны в экспериментах стандартные последовательности радиочастотных импульсов для выполнения таких квантовых логических операций, как отрицание, инверсия фазы, преобразование Адамара и т.п.
Если частота колебаний в импульсах поперечного магнитного поля 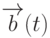 значительно отличается от резонансной для данного спинового кубита, то такие импульсы практически не влияют на состояние этого кубита. Они вызывают лишь незначительные по амплитуде периодические колебания на вынужденной частоте, которые прекращаются после выключения импульса. Это обстоятельство позволило, во-первых, в большинстве случаев упростить генератор поперечного магнитного поля, используя лишь одну пару катушек.
Ведь магнитное поле с линейной поляризацией можно рассматривать как сумму двух полей с круговой поляризацией
значительно отличается от резонансной для данного спинового кубита, то такие импульсы практически не влияют на состояние этого кубита. Они вызывают лишь незначительные по амплитуде периодические колебания на вынужденной частоте, которые прекращаются после выключения импульса. Это обстоятельство позволило, во-первых, в большинстве случаев упростить генератор поперечного магнитного поля, используя лишь одну пару катушек.
Ведь магнитное поле с линейной поляризацией можно рассматривать как сумму двух полей с круговой поляризацией 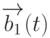 и
и 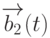 одинаковой амплитуды, вращение в которых происходит в противоположных направлениях. В ПСК вектор
одинаковой амплитуды, вращение в которых происходит в противоположных направлениях. В ПСК вектор 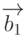 оказывается неподвижным, а вектор
оказывается неподвижным, а вектор 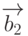 вращается в противоположную сторону с удвоенной угловой скоростью, вследствие чего не влияет на состояние кубита.
вращается в противоположную сторону с удвоенной угловой скоростью, вследствие чего не влияет на состояние кубита.
Во-вторых, тот факт, что радиоимпульсы с частотой, которая не является резонансной, не влияют на состояние кубита, позволяет манипулировать разными кубитами независимо, если их резонансные частоты отличаются на величину, значительно превосходящую частоту Раби.