|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Принципы квантовых вычислений
Кубит – основной элемент квантовой информатики
В классической вычислительной технике обычно используют такие бистабильные элементы, как триггеры, ячейки памяти, логические вентили, в которых другие состояния, кроме двух ("0" или "1"), невозможны или не используются. В классической информатике за единицу количества информации – "бит" – приняли количество информации, которое сохраняется в таком бистабильном элементе.
В квантовой информатике в качестве основного тоже принят квантовый объект, который может находиться в двух различных базовых состояниях. Его назвали "кубит" (от англ. "qubit" – сокращение от "quantum bit" = квантовый бит). Так же назвали и квантовую единицу информации.
Волновые функции кубита в двух его основных ("базовых") состояниях обычно обозначают как  и
и  и называют "базисом". Эти функции всегда нормированы на "1" и "ортогональны" между собой (сокращенно говорят "ортонормированы").
и называют "базисом". Эти функции всегда нормированы на "1" и "ортогональны" между собой (сокращенно говорят "ортонормированы").
Теперь обратите внимание на то, что уравнения Шредингера – как (8.3), так и (8.4) – являются линейными. В том плане, что, если функции  и
и  являются решениями уравнения Шредингера, то и любая их линейная комбинация тоже является его решением. Вследствие этого принципиальной особенностью квантовых объектов, в т.ч. и кубита, является то, что он может находиться не только в двух указанных "базовых" состояниях, но и во многих других состояниях, которые описываются волновой функцией
являются решениями уравнения Шредингера, то и любая их линейная комбинация тоже является его решением. Вследствие этого принципиальной особенностью квантовых объектов, в т.ч. и кубита, является то, что он может находиться не только в двух указанных "базовых" состояниях, но и во многих других состояниях, которые описываются волновой функцией
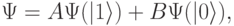 |
( 8.5) |
 на единицу, т.е. условию
на единицу, т.е. условию
 |
( 8.6) |
Такие состояния называют "гибридными" или "смешанными". В классических бистабильных элементах это невозможно, что качественно отличает их от кубитов.
Известно, что комплексные числа  и
и  , которые в квантовой механике называют комплексными амплитудами, можно представить в виде
, которые в квантовой механике называют комплексными амплитудами, можно представить в виде  ,
,  . Тогда выражение (8.5) с учетом условия (8.6) можно переписать в виде:
. Тогда выражение (8.5) с учетом условия (8.6) можно переписать в виде:
 |
( 8.7) |
 – любое действительное число из интервала от – 1 до 1. Значение фазы
– любое действительное число из интервала от – 1 до 1. Значение фазы  не влияет ни на значение
не влияет ни на значение  , ни на выполнение условия нормировки (8.6). Поэтому состояния с разными фазами
, ни на выполнение условия нормировки (8.6). Поэтому состояния с разными фазами  физически различить нельзя, и их считают одним и тем же физическим состоянием. Физически разные состояния кубита описываются волновыми функциями вида
физически различить нельзя, и их считают одним и тем же физическим состоянием. Физически разные состояния кубита описываются волновыми функциями вида
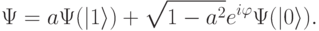 |
( 8.8) |
Каждому из физически различных состояний кубита, заданных формулой (8.8), можно поставить во взаимно однозначное соответствие свой единичный вектор так называемой "сферы Блоха" ( рис. 8.1).

Рис. 8.1. Схематическое изображение множества возможных состояний кубита в виде "сферы Блоха" с радиусом, равным 1
Азимутальный угол  называют "фазой". Если базовым состояниям соответствуют два ортогональных базисных вектора, например, состоянию
называют "фазой". Если базовым состояниям соответствуют два ортогональных базисных вектора, например, состоянию 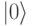 – орт
– орт  оси
оси 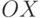 , а состоянию
, а состоянию 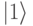 – орт
– орт 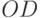 оси
оси 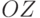 , то указанный на
рис.
8.1 угол
, то указанный на
рис.
8.1 угол  определяется соотношением
определяется соотношением 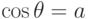 . Выделенному на
рис.
8.1 вектору
. Выделенному на
рис.
8.1 вектору 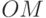 соответствует состояние с волновой функцией
соответствует состояние с волновой функцией
 |
( 8.9) |
Но это – лишь одно из возможных соответствий между точками сферы Блоха и состояниями кубита.
Чаще используют другое, тоже взаимно однозначное соответствие. Оно удобно тем, что базовым состояниям кубита соответствуют не ортогональные, а противоположные орты на сфере Блоха. Исторически сложилось так, что одним из основных вариантов реализации кубита считалось ядро атома со спином, магнитный момент которого в магнитном поле может иметь лишь одну из двух базовых ориентаций: в направлении поля, или против поля. Каждому из гибридных состояний магнитного момента ядра тогда соответствует коллинеарный ему вектор на сфере Блоха. Для этого волновую функцию, соответствующую состоянию кубита, изображенному вектором 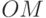 , представляют в виде:
, представляют в виде:
 |
( 8.10) |
При таком представлении базовому состоянию кубита 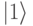 соответствует орт
соответствует орт 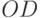 (для него угол
(для него угол  , азимутальный угол
, азимутальный угол  , вообще говоря, не определен, но считается, что
, вообще говоря, не определен, но считается, что 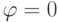 ), а базовому состоянию
), а базовому состоянию 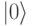 – противоположный орт
– противоположный орт  оси
оси 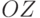 (для него угол
(для него угол  , азимутальный угол
, азимутальный угол  тоже, вообще говоря, не определен, но считается, что
тоже, вообще говоря, не определен, но считается, что 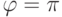 ). Орту
). Орту  оси
оси 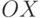 (
( ) соответствует гибридное состояние, которое описывается волновой функцией
) соответствует гибридное состояние, которое описывается волновой функцией
 |
( 8.11) |
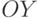 (
( ) – гибридное состояние, которое описывается волновой функцией
) – гибридное состояние, которое описывается волновой функцией
 |
( 8.12) |
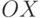 , противоположному к орту
, противоположному к орту  , соответствует гибридное состояние, которое описывается волновой функцией
, соответствует гибридное состояние, которое описывается волновой функцией
 |
( 8.13) |
Точкам на "экваторе" сферы Блоха соответствуют максимально смешанные ("запутанные", "сцепленные") состояния, описываемые волновыми функциями
![\Psi=\frac{\sqrt{2}}{2}\Psi(|1\rangle)e^{-i\varphi} + \frac{\sqrt{2}}{2}\Psi(|1\rangle)e^{i\varphi}],](/sites/default/files/tex_cache/cbb8daca25ab93032ba4afc37933d306.png) |
( 8.14) |
 – произвольная фаза, своя для каждой точки экватора.
– произвольная фаза, своя для каждой точки экватора.Чтобы сделать наглядной принципиальное различие между классическим бистабильным элементом и кубитом, проведем такую аналогию. Элемент изображения (пиксель), соответствующий классическому бистабильному элементу, может быть лишь черным или белым, – даже не полутоновым. А пиксель, соответствующий кубиту, может иметь любой цвет и любые цветовые оттенки! И как цветной пиксель несет намного больше информации, чем черно-белый, так и кубит сохраняет в себе несравненно больше информации, чем один классический бит.
При считывании состояния кубита взаимодействие с устройством считывания изменяет ситуацию. Если устройство считывания является классически бистабильным, т.е. может считывать лишь "0" или "1", и его состояния соответствуют базовым состояниям кубита, то такое устройство однозначно считывает лишь базовые состояния. Любое другое (гибридное) состояние, в котором находится кубит перед считыванием, определяет лишь вероятности считывания "0" и "1":
 |
( 8.15) |
Когда имеется возможность измерять состояние многих идентичных кубитов, находящихся в одинаковых условиях, или многократно считывать состояние одного и того же кубита, который каждый раз перед считыванием приводится в то же самое квантовое состояние, то эти вероятности можно экспериментально найти как относительную частоту считывания того или другого состояния. При этом мы находим величину  , т.е. можем знать проекцию вектора состояния кубита на сфере Блоха лишь на одну из координатных осей. Чтобы определить все проекции вектора состояния, надо провести несколько серий измерений. Процедуру определения истинного состояния кубита называют "томографией квантового состояния".
, т.е. можем знать проекцию вектора состояния кубита на сфере Блоха лишь на одну из координатных осей. Чтобы определить все проекции вектора состояния, надо провести несколько серий измерений. Процедуру определения истинного состояния кубита называют "томографией квантового состояния".
После считывания классически бистабильным устройством кубит согласно правилу редукции остается в том базовом состоянии, которое было считано. Оно совпадает с состоянием кубита перед считыванием только в тех случаях, если это состояние изначально было базовым.
Чтобы сделать интуитивно понятным то, что происходит при "считывании" состояния кубита классическим сенсором, приведем такую аналогию. В день выборов президента Вы пришли на избирательный участок, чтобы проголосовать за одного из двух кандидатов, которые остались в списке. Ни один из них Вас целиком не устраивает, Вы хотели бы иметь другого, лучшего президента. Но в бюллетене для голосования, который Вам выдали, надо выбрать однозначно. Вот Вы и голосуете за одного из кандидатов. Это и есть аналог измерения состояния кубита классическим устройством.
Даже при "считывании" состояния кубита не классическим, а тоже квантовым устройством, вследствие взаимодействия с ним начальное состояние кубита, вообще говоря, изменяется. Математически доказана теорема "о невозможности клонирования квантовых состояний", которая указывает на невозможность копирования произвольного квантового состояния без его изменения. Это возможно исключительно только в базовых состояниях.
Таким образом, в кубите "сохраняется" несравненно больше информации, чем один классический бит, но считать из него классическим прибором можно лишь один бит информации. Внутреннее состояние кубита до считывания определяет лишь вероятность считывания "0" или "1", а после считывания становится таким, которое было считано.
