|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Принципы квантовых вычислений
Основные положения лекции 9
Основным элементом квантового процессора является кубит. Так же называют и соответствующую единицу квантовой информатики. Кубит, как квантовый объект, может находиться не только в двух базовых состояниях 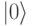 и
и 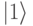 , но и в любом гибридном состоянии. Множество состояний кубита может быть поставлено во взаимно однозначное соответствие с точками сферы единичного радиуса – т.н. сферы Блоха. В наиболее распространенной интерпретации принято, что состоянию
, но и в любом гибридном состоянии. Множество состояний кубита может быть поставлено во взаимно однозначное соответствие с точками сферы единичного радиуса – т.н. сферы Блоха. В наиболее распространенной интерпретации принято, что состоянию 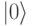 соответствует южный, состоянию
соответствует южный, состоянию 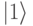 – северный полюс сферы Блоха, а волновая функция кубита в гибридных состояниях описывается выражением
– северный полюс сферы Блоха, а волновая функция кубита в гибридных состояниях описывается выражением
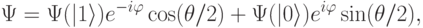
 и
и  – углы сферической системы координат,
– углы сферической системы координат,  и
и  – волновые функции кубита в базовых состояниях, а множители при них – это комплексные числа ("амплитуды").
– волновые функции кубита в базовых состояниях, а множители при них – это комплексные числа ("амплитуды").В кубите "хранится" несравненно больше информации, чем один классический бит, но считать из него классическим прибором можно лишь один бит информации. Вероятности считывания "0" и "1" задаются выражением
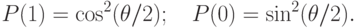
Совокупность слабо связанных кубитов, в которой энергия взаимодействия между кубитами значительно меньше, чем энергия взаимодействия внутри каждого кубита, называют квантовым регистром. Состояния квантового регистра, при которых каждый кубит находится в одном из "базовых" состояний, называют "базисными" и обозначают как  , где каждая переменная принимает значение "0" или "1" и указывает на базовое внутреннее состояние соответствующего кубита. Квантовый регистр из
, где каждая переменная принимает значение "0" или "1" и указывает на базовое внутреннее состояние соответствующего кубита. Квантовый регистр из  кубитов может находиться и во многих других "смешанных" состояниях, которые образуют гильбертово пространство с размерностью
кубитов может находиться и во многих других "смешанных" состояниях, которые образуют гильбертово пространство с размерностью  .
Состояния квантового регистра, которые нельзя описать волновыми функциями отдельных кубитов или нескольких групп кубитов, называют "сплетенными". Оказывая влияние на один или на несколько из взаимосвязанных кубитов, находящихся в сплетенном состоянии, мы вызываем одновременное взаимосогласованное изменение
.
Состояния квантового регистра, которые нельзя описать волновыми функциями отдельных кубитов или нескольких групп кубитов, называют "сплетенными". Оказывая влияние на один или на несколько из взаимосвязанных кубитов, находящихся в сплетенном состоянии, мы вызываем одновременное взаимосогласованное изменение  комплексных чисел (амплитуд). Благодаря этому достигают невиданного в классической информатике параллелизма обработки информации, который с увеличением числа кубитов возрастает экспоненциально.
комплексных чисел (амплитуд). Благодаря этому достигают невиданного в классической информатике параллелизма обработки информации, который с увеличением числа кубитов возрастает экспоненциально.
"Квантовая логика" оказалась несравненно богаче классической. Ведь операндами квантовых логических операций являются не булевы переменные (0 и 1), а квантовые состояния или соответствующие им векторы многомерного пространства. Поэтому и количество возможных вариантов даже однокубитных логических операций бесконечно возрастает. Все однокубитные логические операции имеют своей геометрической интерпретацией определенный поворот вектора состояния кубита на сфере Блоха. Все они могут быть сведены к комбинации лишь двух поворотов: на определенный угол  и на определенный азимутальный угол
и на определенный азимутальный угол  . Наиболее употребительны следующие однокубитные логические операции: инверсия (отрицание); инверсия фазы; преобразование Адамара; запись
. Наиболее употребительны следующие однокубитные логические операции: инверсия (отрицание); инверсия фазы; преобразование Адамара; запись  или
или  .
.
Множество квантовых логических операций над многими кубитами еще мощнее. Выполнение уже одной квантовой логической операции над одним из взаимосвязанных кубитов приводит к изменению состояния всей квантовой системы в целом. Наиболее известной и часто употребляемой многокубитной квантовой логической операцией является "контролируемое отрицание" (Controlled-NOT,  ). В ней один из кубитов считается "управляемым" ("контролируемым"), а другие – "управляющими" ("контролирующими"). Состояние управляемого кубита изменяется на противоположное лишь в том случае, если все управляющие кубиты находятся в базовом состоянии
). В ней один из кубитов считается "управляемым" ("контролируемым"), а другие – "управляющими" ("контролирующими"). Состояние управляемого кубита изменяется на противоположное лишь в том случае, если все управляющие кубиты находятся в базовом состоянии  . Многокубитная квантовая логическая операция Уолша-Адамара переводит квантовый регистр из любого базисного состояния в максимально сплетенное. Часто употребляется также двухкубитная логическая операция обмена квантовых состояний
. Многокубитная квантовая логическая операция Уолша-Адамара переводит квантовый регистр из любого базисного состояния в максимально сплетенное. Часто употребляется также двухкубитная логическая операция обмена квантовых состояний 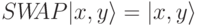 .
.
Обработку информации путем применения квантовых логических операций можно описывать по-разному: как выполнение в определенной последовательности элементарных преобразований (в этом случае говорят о квантовых алгоритмах или программах) или как последовательную обработку потока данных сетью квантовых логических вентилей или "гейтов" (тогда говорят о квантовых схемах). Оба эти подхода, как и в классической вычислительной технике, являются эквивалентными. Считается, что для квантовых вычислений действует тезис Черча-Тьюринга-Дойча: с помощью квантовых логических схем (квантовых алгоритмов) можно смоделировать любой физический процесс, ограниченный в пространстве и во времени.
Разработано уже немало эффективных квантовых алгоритмов для решения таких практически важных задач, как быстрые квантовые преобразования Фурье, факторизация 200-300-значных целых чисел, поиск в неструктурированной базе данных, преобразование числовых матриц больших размеров, нахождение собственных значений и собственных векторов матричных операторов, решение многомерных задач дискретной оптимизации и т.п. Квантовые вычисления значительно эффективнее классических при моделировании поведения многокомпонентных квантовых систем – сложных молекул, химических радикалов, взаимодействий между ними, атомных ядер, других ансамблей из многих элементарных частиц, биологических мембран и др. Во всех этих задачах используются существенные преимущества сплетенных состояний и экспоненциально возрастающий квантовый параллелизм обработки информации в таких состояниях. Поэтому конец ХХ - начало ХХІ в. ознаменовались значительной активизацией исследований и разработок квантовых алгоритмов, подходов к программированию квантовых вычислений, а также путей реализации кубитов и квантовых схем.
Эксперименты уже с первыми действующими образцами квантовых процессоров вывили тот факт, что отдельные кубиты и тем более группы кубитов не удается долго удерживать в "когерентном" состоянии. Как ни стараются экспериментаторы, им не удается полностью исключить влияние хаотических внешних воздействий. Квантовые логические операции тоже не выполняются абсолютно точно. Поэтому и наблюдается постепенная потеря когерентности. В случае взаимодействия многих кубитов, особенно в сплетенных состояниях, это приводит к непредвиденному изменению состояния всего квантового регистра. Такие явления называют "декогерентизацией". Из-за нее в квантовых вычислениях происходят ошибки, и дальше эволюция квантового процессора становится уже неконтролируемой. Однако показано, что с разрушительным влиянием декогерентизации можно успешно бороться с помощью хорошо продуманных методов избыточного кодирования, периодического контроля, своевременного выявления и квантовой коррекции ошибок. Найденные методы позволяют поддерживать контролируемый процесс квантовых вычислений как угодно долго, если вероятность ошибки при выполнении одной квантовой логической операции ниже определенного уровня – порядка одной ошибки на 104–105 квантовых операций.
Для эффективности использования квантовый процессор должен функционировать в комбинации с быстродействующим классическим компьютером. Элементная база квантового процессора должна удовлетворять целому ряду технических требований: не менее чем порядка 1000 кубитов; возможность надежной записи информации в значительное число кубитов и промежуточного считывания состояния некоторых кубитов; выполнение функционально полного набора квантовых логических операций; возможность считывания конечного результата из всей выходной части квантового регистра; время сохранения когерентности должно быть достаточным для выполнения по крайней мере 104–105 квантовых логических операций и др.
Предложены и экспериментально проверены уже десятки вариантов физической реализации кубитов. Их реализуют на основе магнитных моментов электронов и ядер атомов в постоянном магнитном поле ("спиновые кубиты"), на основе дискретных энергетических состояний электронов в "квантовых точках", ионах или атомах, локализованных в определенных местах с помощью специальной конфигурации системы электродов или с помощью т.н. "оптической решетки". Как кубиты могут рассматриваться также и отдельные кванты электромагнитного поля – фотоны видимого или инфракрасного света, импульсы ультракоротких радиоволн, разные "моды" акустических колебаний и т.п. Предложены и исследуются много вариантов и совсем "экзотических" кубитов.
Набор для практики
Вопросы для самоконтроля
- Что такое "кубит"? Чем он отличается от классических бистабильных элементов?
- Что такое "сфера Блоха"? Каково наиболее употребляемое соответствие между состояниями кубита и точками на сфере Блоха? Напишите соответствующие формулы.
- Что происходит при считывании информации с кубита классическим бистабильным устройством? Запишите формулы для вероятностей считывания "0" и "1".
- Чем квантовый регистр отличается от классического?
- Что такое "сплетенные состояния"? Как они связаны с параллелизмом обработки информации и как он возрастает с увеличением числа кубитов в квантовом регистре?
- Какие однокубитные квантовые логические операции Вы знаете? Расскажите, как действуют наиболее употребляемые из них.
- Какую геометрическую интерпретацию имеют однокубитные квантовые логические операции? Дайте такую интерпретацию однокубитным квантовым логическим операциям отрицания, инверсии фазы, преобразованию Адамара.
- В чем заключается двухкубитная квантовая логическая операция SWAP?
- В чем заключается многокубитная квантовая логическая операция "контролируемое отрицание"? Начертите схему квантового логического вентиля .
- В чем заключается многокубитная квантовая логическая операция Уолша-Адамара?
- В чем заключается квантовая логическая операция Тоффоли?
- В чем состоит разница между квантовыми алгоритмами и квантовыми логическими схемами?
- Что утверждает тезис Черча-Тьюринга-Дойча?
- Для чего предназначены квантовые алгоритмы П. Шора и Л. Гровера? На чем основана их эффективность?
- Что такое "декогерентизация"? К чему она приводит?
- Имеются ли пути обеспечения надежности квантовой обработки информации? Какие для этого надо выполнить условия?
- Можете ли Вы начертить функциональную схему электронного комплекса для квантовых вычислений? Расскажите в общих чертах, как этот комплекс функционирует.
- Каким техническим требованиям должна удовлетворять элементная база квантового процессора?
- Какие варианты физической реализации кубитов Вы можете назвать?
