Нормализация

5.13 Зависимости соединения и пятая нормальная форма. Правило приведения

Бегло рассмотрим дальнейшее обобщение понятия функции до зависимости проекция-соединение. На его основе определим пятую нормальную форму и правила приведения к ней.

4НФ не дает полного решения вопроса о декомпозиции отношений без потерь информации. Причина в том, что рассмотрения декомпозиции только на два отношения недостаточно. Может существовать нетривиальная декомпозиция на три отношения, но не существовать такой декомпозиции на два отношения.

Ниже на рисунке 5.9 приведен пример отношения, которое нельзя восстановить после разложения на две части, но например, соединение, 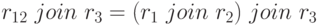восстанавливает отношение. Оказалось необходимым использование соединения трех проекций.

Рис. 5.9. Отношение, восстанавливаемое соединением трех проекций

То, что отношение восстанавливается соединением всех трех проекций, но не любых двух, означает что между атрибутами отношения имеется зависимость, которую нельзя считать функциональной или многозначной.

Определение (зависимость соединения). Пусть - отношение на множествах атрибутов 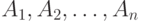, может быть пересекающихся. Отношение удовлетворяет зависимости соединения тогда и только тогда, когда оно равносильно соединению всех своих проекций на подмножества атрибутов 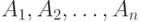, то есть

.

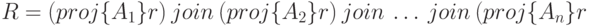Обозначение зависимости соединения .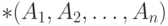

Зависимость соединения обобщает MV-зависимости. Если в отношении имеется многозначная зависимость, то имеется и зависимость соединения. Обратное неверно.

Связь расширений функциональной зависимости определяет

Теорема 5.2. Отношение со схемой 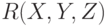удовлетворяет зависимости соединения тогда и только тогда, когда имеется многозначная зависимость .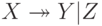

Для того, чтобы сформулировать определение пятой нормальной формы, разберемся с понятием тривиальной зависимости соединения.

Определение (тривиальная зависимость соединения). Зависимость 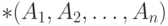называется тривиальной зависимостью соединения, если выполняется одно из условий:

1. все множества атрибутов 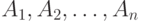содержат потенциальный ключ отношения ;
2. одно из множеств 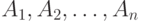совпадает со всем множеством атрибутов отношения .

Определение (5НФ). Отношение находится в пятой нормальной форме (5НФ) тогда и только тогда, когда любая имеющаяся зависимость соединения тривиальна.

Правило приведения к 5НФ: Если в отношениях обнаружены нетривиальные зависимости соединения, то для их исключения необходимо провести декомпозицию на выделенные подмножества атрибутов .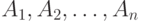

5.14 Понятие о нормальной форме домен-ключ

Рассмотрим определение нормальной формы домен-ключ, играющей важную роль в теории и ограничивающую дальнейшие поиски нормальных форм.

Определение (НФДК, DKNF). Отношение находится в нормальной форме домен-ключ, если каждое ограничение отношения есть логическое следствие определений ключей и доменов.

Р. Фейгин доказал, что отношение в нормальной форме домен-ключ не имеет никаких аномалий модификации и, с другой стороны, отношение не имеющее аномалий модификации находится в нормальной форме домен-ключ. Уточним список понятий, использованных в определении НФДК.

Ограничение - это правило заданное для статических значений атрибутов с помощью

• функциональных зависимостей,
• многозначных зависимостей,
• ограничений на значения атрибутов,
• ограничений типа бизнес-правил.

Домен - это множество допустимых значений. Он содержит:

• описание физического уровня,
• описание логического уровня.

Вспомним, что в реляционной модели данных смыслы данных ограничиваются заданием ограничений целостности (первичных, уникальных, альтернативных ключей, ограничений типа check) и определениями доменов. Понятно, что НФДК можно трактовать как условие, определяющее возможность адекватной передачи смыслов данных из концептуальной модели в реляционную или связанные с ней модели.

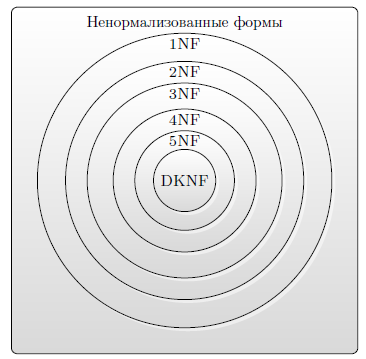
И, в заключение, рисунок 5.10, определяющий соотношение между нормальными формами.

Рис. 5.10. Нормальные формы

5.15 Понятие о денормализации

Как известно, база данных - это не только то, что в ней содержится, но и то, что в ней можно спросить и что фактически спрашивают.

Анализ потока запросов может показать, что схема нормализованной базы нуждается в преобразовании, не соответствующем требованиям нормализации. Такие преобразования называют денормализацией.

Как правило, денормализация ускоряет запросы, но замедляет манипулирование данными и усложняет, может быть существенно, процедурную часть приложения.

Рассмотрим пример преобразования называемого сверхномализацией. Поскольку временные свойства уместно обсуждать только в рамках некоторой реализации, будем говорить о таблицах. Проблемными, в соответствиисо сложившейся практикой администрирования баз данных, будем называть таблицы, поток запросов к которым существенно загружает процессор.

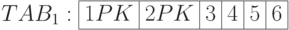
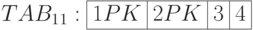
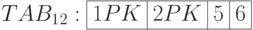
Пусть обнаружено, что запросы к проблемной таблице TAB₁ обращаются чаще к коротким столбцам 1, 2, 5, 6 шириной, например, по 5 байт, чем к широким столбцам 3 и 4 шириной 12 кбайт и 64 кбайт, соответственно. Ключ образуют столбцы 1 и 2. Понятно, что для извлечения 20-ти байт приходится работать со всей строкой шириной примерно 76 кбайт. Это сильно тормозит процесс.

Проведем денормализацию. Разделим таблицу на две - TAB₁₁, включающую широкие столбцы 3, 4, и TAB₁₂ с узкими столбцами. Ключ у новых таблиц тот же. Скорость запросов возрастет, так как теперь не нужно извлекать "лишних" 76 килобайт на каждую строку. Однако, теперь вместо одной команды вставки, удаления и обновления исходной таблицы необходимо выполнять по две соответствующих команды для TAB₁₁ и TAB₁₂, причем обе команды должны быть выполнены обязательно. В "Транзакции в базах данных" станет понятно, что для этого необходимо вставить их в транзакцию.

Если поток запросов изменится, то выполненное преобразование схемы может оказаться бесполезным и даже вредным.