| Россия |
Нормализация
5.11 Многозначные зависимости. Теорема Фейгина
Займемся многозначными зависимостями возникающими при приведении в 1НФ отношений с двумя и более многозначными атрибутами. К определению четвертой нормальной формы придем через обобщение понятия функции, заданной на отношении, до многозначной функциональной зависимости. Обобщение теоремы Хиса на такие зависимости называется теоремой Фейгина. Она определяет правило приведения к четвертой нормальной форме. Рассмотрим отношение, в котором курс может считать не один лектор, но для каждого лектора обязателен один и тот же набор учебников, обозначенных по фамилиям авторов (таблица 5.10). Имейте в виду, что такие авторы, как Чучкин, Пупкин, Малинин и Буренин когда-то существовали.
| ДИСЦИПЛИНА | ЛЕКТОР | УЧЕБНИК |
| Арифметика | Иванов Петров | Чучкин & Пупкин Малинин & Буренин |
| Генетика | Карпов | Вайсман Лысенко |
| РК |
Лектор и учебник независимы в том смысле, что возможны, любые их сочетания. Преобразуем отношение в 1НФ (таблица 5.11). С одной стороны получена НФБК, так как ключ охватывает все кортежи и возможны только тривиальные зависимости. С другой стороны, налицо избыточность. Имеются аномалии по включению (одного лектора включаем столько раз, сколько имеется учебников) и по удалению (при удалении лектора необходимо удалить столько строк, сколько имеется учебников).
| ДИСЦИПЛИНА | ЛЕКТОР | УЧЕБНИК |
| Арифметика | Иванов | Чучкин & Пупкин |
| Арифметика | Иванов | Малинин & Буренин |
| Арифметика | Петров | Чучкин & Пупкин |
| Арифметика | Петров | Малинин & Буренин |
| Генетика | Карпов | Вайсман |
| Генетика | Карпов | Лысенко |
| РК | ||
Многозначные зависимости (multi-valued dependency) возникают, когда необходимо привести к первой нормальной форме отношение с независимыми многозначными атрибутами, имеющими несколько значений на пересечении строки и столбца. Пусть имеется два таких атрибута  и
и  . Тогда для получения 1НФ необходимо для каждого набора значений остальных атрибутов
. Тогда для получения 1НФ необходимо для каждого набора значений остальных атрибутов  повторить эту строку для каждого сочетания атомарного значения
повторить эту строку для каждого сочетания атомарного значения  с каждым атомарным значением
с каждым атомарным значением  .
.
Образуется многозначная зависимость, в которой:
- каждому значению
 соответствует набор значений
соответствует набор значений  ;
; - каждому значению
 соответствует набор значений
соответствует набор значений  ;
; - значения атрибутов
 и
и  не зависят один от другого.
не зависят один от другого.
Многозначную зависимость принято обозначать 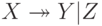 , хотя можно было бы указать наличие двух существующих одновременно обычных функциональных зависимостей
, хотя можно было бы указать наличие двух существующих одновременно обычных функциональных зависимостей 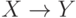 и
и 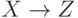 . Иногда обозначают многозначную зависимость
. Иногда обозначают многозначную зависимость  или
или 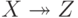 .
.
Определение. MV-зависимость  называется тривиальной если
называется тривиальной если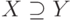 , либо
, либо 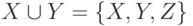 .
.
Рассмотрим еще одно отношение с многозначными зависимостями (рисунок 5.17). Обозначения: 3 - завод, Т - товар, М - магазин. Выполняется условие: каждый товар из группы товаров продается во все магазины из некоторой группы магазинов. При этом и в группе товаров и в группе магазинов может быть один экземпляр. Исходное отношение ЗТМ разлагается на отношения ЗТ и ЗМ. В отличие от первых четырех нормальных форм связи между созданными отношениями (ЗТ и ЗМ) отсутствуют.
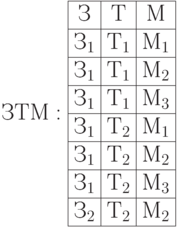
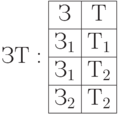
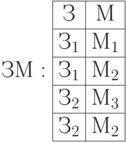
Определение (MV-зависимость). Пусть  - отношение, а
- отношение, а 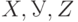 - непересекающиеся множества его атрибутов. Атрибуты
- непересекающиеся множества его атрибутов. Атрибуты  и
и  многозначно зависят от
многозначно зависят от  (обозначение
(обозначение 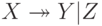 ) если из того, что в отношении
) если из того, что в отношении  содержатся кортежи
содержатся кортежи 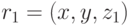 и
и 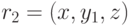 , следует, что в отношении
, следует, что в отношении  содержится также кортеж
содержится также кортеж 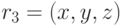 .
.
По симметрии определения в  содержится и кортеж
содержится и кортеж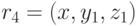 . Атрибуты
. Атрибуты  и
и  как бы симметричны по отношению к
как бы симметричны по отношению к  .
.
При наличии MV-зависимости кортежи обязаны вставляться и удаляться одновременно целыми наборами.
Теорема Фейгина (R. Fagin) играет для многозначных зависимостей ту же роль, что теорема Хиса для функциональных зависимостей. Примем ее без доказательства.
Теорема Фейгина. Пусть 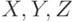 - три непересекающиеся подмножества атрибутов
- три непересекающиеся подмножества атрибутов 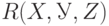 отношения
отношения  . Декомпозиция отношения г на проекции на множества атрибутов
. Декомпозиция отношения г на проекции на множества атрибутов 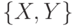 и
и 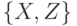 будет декомпозицией без потерь тогда и только тогда, когда имеется многозначная зависимость
будет декомпозицией без потерь тогда и только тогда, когда имеется многозначная зависимость 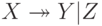 .
.
Частный случай. Если зависимость 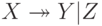 является тривиальной, т.е. существует только одна из функциональных зависимостей
является тривиальной, т.е. существует только одна из функциональных зависимостей 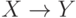 или
или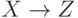 , но не задана независимость
, но не задана независимость  и
и  , то получаем теорему Хиса.
, то получаем теорему Хиса.
5.12 Четвертая нормальная форма. Правило приведения
Определение (4НФ). Отношение находится в четвертой нормальной форме, если оно находится в нормальной форме Бойса-Кодда и не содержит нетривиальных многозначных зависимостей.
Отношения с нетривиальными многозначными зависимостями могут появиться при хранении в одном отношении двух независимых сущностей. Такое отношение образуется как естественное соединение двух отношений по атрибутам, которые не составляют ключа в исходных отношениях.
Правило приведения к 4НФ: Если в отношении находящемся в НФБК обнаружены нетривиальные многозначные зависимости, то для их исключения необходимо провести декомпозицию используя теорему Фейгина.
Полученные после декомпозиции отношения никак не связаны между собой.
Теперь к правилам приведения до НФБК, изложенным в разделе 5.10, можно добавить только что сформулированное правило, может быть, уточнив, что возможен вариант использования не 1НФ а Н1НФ.
На рисунке 5.8 приведена мнемоника для правил приведения к первым пяти нормальным формам. Считалочка для запоминания: "Ключ, весь ключ и ничего кроме ключа". Как присяга - правду, всю правду и ничего кроме правды! Крестом отмечены виды функциональных зависимостей, которые должны быть устранены.