|
Добрый день!
Скажите, пожалуйста,планируется ли продолжение курсов по нанотехнологиям? Спасибо, Евгений
|
Оценка производительности и живучести МКМД-БИТ-потокового предпроцессора системы астронавигации
8.2. Потоковый алгоритм работы МКМД-бит-потокового субпроцессора слежения за центром масс астроориентира
Все рассмотренные процедуры работы канала обработки видеоизображения необходимо привести к потоковому виду, который учитывает как "непрерывность" потока входных и выходных данных, так и специфику работы МКМД-бит-потоковых субпроцессоров, которая связана с тем, что каждая потоковая слов-инструкция пользователя интерпретируется МКМД-бит-процессорной матрицей. Поэтому ее необходимо сопроводить индивидуальными средствами управления, задающими и реализующими циклы  и
и  , где
, где  и
и  - соответственно разрядность арифметики и количество операндов в циклически обрабатываемых потоках данных. В результате на ассемблерном уровне организации вычислений выдерживается принцип "одна инструкция - один процессор", который в каждой ассемблерной команде поддерживается своими специфическими входными и выходными интерфейсами, устройствами управления и обработки. С целью повышения отказоустойчивости и отказобезопасности МКМД-бит-потокового субпроцессорного тракта обработки видеоизображений необходимо выбрать и включить в него процедуры генерации избыточных данных и устройств обнаружения отказов темпа реального времени. В результате потоковый алгоритм работы такого многопроцессорного устройства принимает вид:
- соответственно разрядность арифметики и количество операндов в циклически обрабатываемых потоках данных. В результате на ассемблерном уровне организации вычислений выдерживается принцип "одна инструкция - один процессор", который в каждой ассемблерной команде поддерживается своими специфическими входными и выходными интерфейсами, устройствами управления и обработки. С целью повышения отказоустойчивости и отказобезопасности МКМД-бит-потокового субпроцессорного тракта обработки видеоизображений необходимо выбрать и включить в него процедуры генерации избыточных данных и устройств обнаружения отказов темпа реального времени. В результате потоковый алгоритм работы такого многопроцессорного устройства принимает вид:
Шаг 1. Перевести поток 16-битных входных операндов из параллельного кода  в последовательный код
в последовательный код  . Здесь
. Здесь  , а перечисление потока входных данных происходит по строкам исходного изображения. Такой перечислительный процесс осуществляется внешними по отношению к субпроцессору аппаратными средствами, реализующими три вложенных цикла:
, а перечисление потока входных данных происходит по строкам исходного изображения. Такой перечислительный процесс осуществляется внешними по отношению к субпроцессору аппаратными средствами, реализующими три вложенных цикла:  , где индекс кадра обрабатываемого изображения
, где индекс кадра обрабатываемого изображения  , a
, a  ;
;  .
.
Во входном интерфейсе самого МКМД-бит-потокового субпроцессора реализуется "бесконечно кратный" цикл  , который соответствует циклу перехода от параллельного кода к последовательному с использованием 16-разрядной шины данных.
, который соответствует циклу перехода от параллельного кода к последовательному с использованием 16-разрядной шины данных.
Шаг 2. Заместить две верхние и две нижние строки в каждом кадре исходного изображения  тестовыми данными (рис. 8.3) по правилу: "пять единиц - три ноля", "пять единиц - три ноля" и т. д., всего 64 раза. В субпроцессоре тестовой считается та фаза вычислений, в которой в "скользящем окне" медианного фильтра объединяются две нижние строки из предыдущего кадра с двумя верхними строками из текущего кадра обрабатываемого изображения. В результате на выходе медианного фильтра будет выработано по 3 "единицы" на каждые 8 пикселей, то есть эталонная тестовая реакция канала логической обработки на этот фрагмент изображения должна равняться 48.
тестовыми данными (рис. 8.3) по правилу: "пять единиц - три ноля", "пять единиц - три ноля" и т. д., всего 64 раза. В субпроцессоре тестовой считается та фаза вычислений, в которой в "скользящем окне" медианного фильтра объединяются две нижние строки из предыдущего кадра с двумя верхними строками из текущего кадра обрабатываемого изображения. В результате на выходе медианного фильтра будет выработано по 3 "единицы" на каждые 8 пикселей, то есть эталонная тестовая реакция канала логической обработки на этот фрагмент изображения должна равняться 48.
Чтобы осуществить замещение двух верхних и двух нижних строк исходного изображения тест-данными, необходимо:
- реализовать цикл
 который определяется размерами обрабатываемого изображения 128*128 однобитных пикселей;
который определяется размерами обрабатываемого изображения 128*128 однобитных пикселей; - реализовать цикл
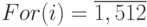 , который определяется размерами 4-х тестовых строк;
, который определяется размерами 4-х тестовых строк; - реализовать циклическую константу вида
 , которая подставляется вместо текущих во время одного цикла
, которая подставляется вместо текущих во время одного цикла 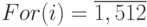 ;
; - задать начальную фазу поступления входных данных таким образом, чтобы цикл
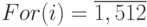 совместился с двумя нижними и двумя верхними строками обрабатываемого изображения.
совместился с двумя нижними и двумя верхними строками обрабатываемого изображения.
Шаг 3. Обработать полученное изображение медианным фильтром размером 5*5 пикселей:  . Здесь:
. Здесь:
-
 - индексы элементов, соответствующие одному положению "скользящего окна";
- индексы элементов, соответствующие одному положению "скользящего окна"; - индексы
 соответствуют центральному элементу "скользящего окна" размером 5*5 пикселей, и они связаны с индексами строк и столбцов исходного изображения
соответствуют центральному элементу "скользящего окна" размером 5*5 пикселей, и они связаны с индексами строк и столбцов исходного изображения  правилом:
правилом:  , а
, а  , где
, где  - координаты левого верхнего угла "скользящего окна".
- координаты левого верхнего угла "скользящего окна".
В МКМД-бит-потоковых технологиях процедура "скольжения" окна размером 5*5 пикселей реализуется с помощью FIFO -регистровой линии задержки, имеющей 1 вход и 25 выходов, на которых одновременно появляются все элементы, соответствующие текущему положению "скользящего окна". Фактически такая линия^ задержки реализует 5 вложенных циклов:  ,где
,где 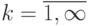 ;
;  ;
;  ;
;  ;
;  .
.
Обычно медианная фильтрация выполняется через две логические процедуры:
- упорядочение элементов
 по возрастанию;
по возрастанию; - присвоение
 , которое соответствует выбору центрального элемента в упорядоченной последовательности
, которое соответствует выбору центрального элемента в упорядоченной последовательности  .
.
Но в данном случае мы имеем дело с бинарным изображением, и поэтому медианную фильтрацию можно выполнить через две арифметико-логические процедуры:

В МКМД-бит-потоковых технологиях невозможно непосредственно просуммировать однобитный поток данных, так как "единица переноса" сохраняется внутри бит-процессора (БП) и учитывается на следующем такте суммирования (см. рис. 3.2 раздела 3.1). Поэтому приходится:
- разделять поток входных бит-данных сначала на два потока, в один из которых попадают все четные, а в другой - все нечетные биты из суммируемого потока;
- выравнивать по времени задержки на 1 такт и суммировать четные и нечетные биты одного и того же входного потока;
- разбивать поток 2-битных частных сумм на два потока - четный и нечетный, и, выровняв их по времени задержки на 2 такта, суммировать и т. д. до получения промежуточного операнда, разрядность которого обеспечивает накопление всей суммы;
- сложение частных сумм по классической схеме с накапливающим аккумулятором.
Для суммирования по этой схеме необходимо реализовать (в данном случае) 6 вложенных циклов:  , из которых 5 нижних используются для формирования 32-битных операндов, обеспечивающих нулевую погрешность вычислений взвешенных сумм в последующих процедурах, а
, из которых 5 нижних используются для формирования 32-битных операндов, обеспечивающих нулевую погрешность вычислений взвешенных сумм в последующих процедурах, а  ;
; 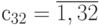 ;
;  ;
;  ;
;  ;
;  .
.
Шаг 4. Обнулить реакцию медианного фильтра на паразитные взаимодействия элементов "скользящего окна" при его переходе со строки на строку (со столбца на столбец):

где  , если
, если  , и
, и  в противном случае.
в противном случае.
Для выполнения этого шага потокового алгоритма необходимо:
- задать цикл обработки строки
 ;
; - сформировать циклическую константу вида: 4 бита - "нули" и остальные 124 бита - "единицы".
Шаг 5. Составить гистограммы по строкам 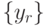 или по столбцам
или по столбцам  ,
,
где


Для реализации этих выражений необходимо:
- задать цикл обработки строки
 ;
; - сформировать циклическую константу вида: 32 "единицы" и 32 "нуля";
- сформировать циклическую константу вида: 32 бита - "единицы" и 16352 бита - "нули", а также ее инверсию для управления циклом накопления.
Шаг 6. Обработать полученные гистограммы 2-элементным "скользящим окном":  или
или  .
.
Данная процедура выполняется "непрерывно" и не налагает каких-либо ограничений на процедуру парного суммирования.
Шаг 7. Сравнить результат обработки первых и последних двух тестовых строк кадра с эталонной реакцией:

Для выполнения этого шага потокового алгоритма необходимы те же управляющие процедуры, что и на шаге 6.
Шаг 8. Обнулить реакцию 2-элементного "скользящего окна" на паразитные взаимодействия элементов при переходе от одного кадра обрабатываемого изображения к другому:
 и
и 
где  , если
, если  , и
, и  , если
, если 
Для выполнения этого шага потокового алгоритма необходимо выполнить те же управляющие процедуры, что и на шаге 6.
Шаг 9. Выполнить "свертку" вектор-столбца 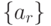 и вектор-строки
и вектор-строки  по правилу:
по правилу:

Здесь  - весовые коэффициенты, соответствующие индексу элемента вектор-столбца или элемента вектор-строки -
- весовые коэффициенты, соответствующие индексу элемента вектор-столбца или элемента вектор-строки -  и
и  соответственно.
соответственно.
Для выполнения этого шага потокового алгоритма необходимо выполнить те же управляющие процедуры, что и на шаге 6.
Шаг 10. Вычислить суммарную "яркость" обрабатываемого изображения:

Для выполнения этого шага потокового алгоритма необходимо выполнить те же управляющие процедуры, что и на шаге 6.
Шаг 11. Определить координаты  центра масс изображения по отношению к его верхнему левому углу:
центра масс изображения по отношению к его верхнему левому углу:  и
и  .
.
Шаг 12. Определить координаты  центра масс изображения по отношению к его центру:
центра масс изображения по отношению к его центру:  и
и  ;
;  ;
; 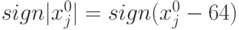 .
.
Шаг 13. Продублировать вычисления на шагах 8-11 с использованием дополнительного комплекта аппаратуры и сравнить результат с основным:

В МКМД-бит-потоковых вычислительных технологиях последние три процедуры выполняются над "бесконечными" потоками данных, из которых только один цикл является информативным, который и выделяется интерфейсом обмена с последующим устройством обработки.
Из приведенных данных видно, что практически в каждой потоковой процедуре необходимо определить параметры циклов 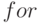 , которые необходимо заложить в управляющие конструкции, специфичные для каждой словинструкции. Именно индивидуальные процедуры управления "по счетчику" (циклы
, которые необходимо заложить в управляющие конструкции, специфичные для каждой словинструкции. Именно индивидуальные процедуры управления "по счетчику" (циклы 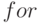 ) отличают МКМД-бит-потоковые субпроцессоры от остальных программируемых средств вычислительной техники. Объясняется это тем, что это класс субпроцессоров работает в режиме интерпретации, а не компиляции прикладных программ. В традиционных архитектурах режим интерпретации значительно проигрывает во времени режиму компиляции, так как в этом случае все аппаратные ресурсы процессора последовательно предоставляются каждой инициализированной слов-инструкции, что вынуждает перенастраивать процессор на параметры каждой инициализированной инструкции ассемблера. В случае бит-потоковых субпроцессоров режим интерпретации не сопряжен с
большими временными издержками, так как все управляющие и интерфейсные процедуры реализуются аппарат-но и включают в себя параметры циклов управления. Это приводит к росту аппаратных затрат на средства управления вычислительным процессом, но обеспечивает максимальную "мобильность" микропрограммных модулей на бит-матрице в процессе парирования множественных карт отказов.
) отличают МКМД-бит-потоковые субпроцессоры от остальных программируемых средств вычислительной техники. Объясняется это тем, что это класс субпроцессоров работает в режиме интерпретации, а не компиляции прикладных программ. В традиционных архитектурах режим интерпретации значительно проигрывает во времени режиму компиляции, так как в этом случае все аппаратные ресурсы процессора последовательно предоставляются каждой инициализированной слов-инструкции, что вынуждает перенастраивать процессор на параметры каждой инициализированной инструкции ассемблера. В случае бит-потоковых субпроцессоров режим интерпретации не сопряжен с
большими временными издержками, так как все управляющие и интерфейсные процедуры реализуются аппарат-но и включают в себя параметры циклов управления. Это приводит к росту аппаратных затрат на средства управления вычислительным процессом, но обеспечивает максимальную "мобильность" микропрограммных модулей на бит-матрице в процессе парирования множественных карт отказов.

