|
Добрый день!
Скажите, пожалуйста,планируется ли продолжение курсов по нанотехнологиям? Спасибо, Евгений
|
МКМД-БИТ-потоковые субпроцессоры с (микро)программируемой архитектурой
4.5. Порядок синтеза МКМД-бит-потоковых субпроцессорных трактов
Область задач, где МКМД-бит-потоковые вычислительные технологии гарантируют системотехнический выигрыш перед остальными вычислительными технологиями, задается тремя противоречивыми требованиями, требующими одновременного удовлетворения:
- вытекающая из условий реального времени решаемых задач пропускная способность по потокам инструкций (производительность -
 ) (и/или данных -
) (и/или данных -  ) должна намного превосходить предоставляемую отдельным (бит)процессором физическую пропускную способность по потокам инструкций (
) должна намного превосходить предоставляемую отдельным (бит)процессором физическую пропускную способность по потокам инструкций (  ) (и/или данных -
) (и/или данных -  ):
):  ;
; - "время жизни" (сверх)многопроцессорной (Б)ВС должно быть на 1-2 порядка больше времени наработки на один отказ одной комплектующей СБИС;
- (сверх)многопроцессорная (Б)ВС должна быть абсолютно устойчивой по своим вычислительным характеристикам, то есть она должна вносить нулевой вклад в абсолютную и/или относительную погрешность вычислений по отношению к погрешности представления исходных данных.
Из перечисленных требований первое является доминирующим, так как при  обычно имеется достаточный аппаратно-временной резерв, чтобы удовлетворить два оставшихся требования с использованием хорошо отработанных традиционных методов и средств аппаратно-временной избыточности. Специфика работы (Б)ВС для боевых ЛА как раз и состоит в том, что подавляющее большинство решаемых задач выдвигает к оборудованию полный комплекс перечисленных выше противоречивых требований, проявляющийся в жесткой "борьбе" за общий аппаратно-временной ресурс (Б)ВС. Поэтому в условиях прототипирования, где решающую роль играет качество синтеза прообраза создаваемого ЛА, такую же решающую роль играет точная и достоверная оценка потребной и предоставляемой производительности на самых ранних этапах проведения проектных работ. Но хроническая проблема всей вычислительной техники как раз и состоит в том, что, отталкиваясь от формальных моделей решаемых задач, точно и достоверно можно определить только прямые алгоритмические затраты некоторой абстрактной вычислительной машины, способной выполнить полный набор требуемых арифметико-логических действий и управляющих процедур, связанных с порядком перечисления
обычно имеется достаточный аппаратно-временной резерв, чтобы удовлетворить два оставшихся требования с использованием хорошо отработанных традиционных методов и средств аппаратно-временной избыточности. Специфика работы (Б)ВС для боевых ЛА как раз и состоит в том, что подавляющее большинство решаемых задач выдвигает к оборудованию полный комплекс перечисленных выше противоречивых требований, проявляющийся в жесткой "борьбе" за общий аппаратно-временной ресурс (Б)ВС. Поэтому в условиях прототипирования, где решающую роль играет качество синтеза прообраза создаваемого ЛА, такую же решающую роль играет точная и достоверная оценка потребной и предоставляемой производительности на самых ранних этапах проведения проектных работ. Но хроническая проблема всей вычислительной техники как раз и состоит в том, что, отталкиваясь от формальных моделей решаемых задач, точно и достоверно можно определить только прямые алгоритмические затраты некоторой абстрактной вычислительной машины, способной выполнить полный набор требуемых арифметико-логических действий и управляющих процедур, связанных с порядком перечисления
потоков инструкций и данных. Определить реальное количество операций, затрачиваемых на решение конкретной задачи даже при полностью известном алгоритме, удается только в отдельных простейших случаях.
Объясняется это тем, что в общем случае потоки инструкций и данных являются частично упорядоченными на оси времени, так как в вычислительных алгоритмах решаемых задач широко используются операторы условных переходов. Именно наличие в программах обработки операторов условных переходов делает взаимозависимыми процессы перечисления потоков инструкций и данных. Избавиться от такой взаимной зависимости практически невозможно, так как при написании алгоритмов и программ в подавляющем большинстве случаев известны только условия перехода или завершения цикла, зависящие от содержимого обрабатываемых потоков данных, но не момент наступления этого события. Отсюда видно, что объективно существующая в вычислительных алгоритмах PD -ассоциативная зависимость между потоками инструкций и данных, с одной стороны, упрощает задачу управления в темпе реального времени в (сверх)больших коллективах вычислителей, а с другой стороны, она не позволяет оценить точное количество инструкций, которые необходимо реально исполнить, чтобы на заданном интервале времени решить поставленную вычислительную задачу.
В МКМД-бит-потоковых вычислительных технологиях такая взаимозависимость между потоками инструкций и данных не устраняется, а только разрывается за счет того, что в ней аппаратно поддержаны только поток-операторы с линейным (инкрементным) порядком перечисления потока ассемблерных слов-инструкций с заранее известным количеством циклов их исполнения. Нелинейный и зависящий от содержимого обрабатываемых данных порядок перечисления реально исполняемых ассемблерных слов-инструкций реализуется на уровне задач, где неделимой единицей управления являются исполняемые поток-операторы и циклически преобразуемые ими потоки данных. В рамках активизированного поток-оператора порядок исполнения слов-инструкций строго задан, а количество циклов их исполнения задается по счетчику, а не по условию. При этом количество циклов исполнения самого поток-оператора считается бесконечным, а переход к другому поток-оператору может быть осуществлен по условию, проверяемому контроллером (суб)процессорного тракта после каждого цикла исполнения поток-оператора над выборкой из 
 -битных данных (см.
рис. 4.5), то есть с достаточно продолжительным периодом из
-битных данных (см.
рис. 4.5), то есть с достаточно продолжительным периодом из 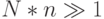 тактов.
тактов.
В таких условиях оценка алгоритмических затрат дает минимальную нижнюю границу, отталкиваясь от которой, уже можно оценить реальные аппаратно-временные затраты, учитывающие и системные издержки на организацию вычислений. С этой целью в МКМД-бит-потоковых вычислительных технологиях необходимо:
- Отталкиваясь от формализованного алгоритма и архитектуры абстрактной вычислительной машины, оценить количество операций, затрачиваемых на реализацию основных, управляющих и коммутационных функций.
- Опираясь на полученное распределение операционных затрат, откор-ректировать абстрактную базовую архитектуру так, чтобы обеспечить равную продолжительность цикла (в числе тактов) исполнения всех процедур, используемых при выполнении основных, управляющих и коммутационных функций.
- Представить в потоковом виде вычислительный алгоритм для всех операционных, управляющих, адресных и коммутационных процедур, с явным указанием требуемого уровня векторно-конвейерного распараллеливания для каждой из них.
- Используя библиотеку стандартных слов-инструкций, синтезировать топологию микропрограмм для всех поток-операторов решаемой задачи и на ее основе определить аппаратно-временные затраты и время задержки в (суб)процессоре.
- Оценить полученные в пункте 4 результаты в целом для комплекса БЭО и всего ЛА и при необходимости повторить шаги 1-5 с модифицированной алгоритмической и векторно-конвейерной схемой распараллеливания вычислений.
Отличительная особенность МКМД-бит-потоковых технологий состоит в том, что они позволяют в таком итеративном процессе последовательного приближения предоставляемой производительности к требуемой достаточно быстро модифицировать не только архитектуру синтезируемого (суб)процессора, но и микропрограммные процедуры исполнения всех используемых слов-инструкций, состав и порядок реализации которых в остальных, в том числе и в RISC -технологиях, неизменен.
Таким образом, целевую функцию итеративного процесса проектирования МКМД-бит-потоковых субпроцессоров можно представить:  , а интерактивные методы и средства достижения этой цели в качестве ограничений используют структурно-функциональные возможности бит-процессоров и схемотехнические характеристики комплектующих СБИС.
, а интерактивные методы и средства достижения этой цели в качестве ограничений используют структурно-функциональные возможности бит-процессоров и схемотехнические характеристики комплектующих СБИС.
В качестве примера оценим потребную производительность при решении задачи медианной фильтрации [290] исходного изображения размером  полутоновых черно-белых пикселей
полутоновых черно-белых пикселей 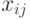 "скользящим окном"
"скользящим окном"  (рис. 4.17 ). Медианный фильтр является частным случаем рангового фильтра и реализует преобразование подстановки центральному элементу "скользящего окна" исходного изображения
(рис. 4.17 ). Медианный фильтр является частным случаем рангового фильтра и реализует преобразование подстановки центральному элементу "скользящего окна" исходного изображения  значение
значение  , вычисленное по всем
, вычисленное по всем  , где
, где  - центральный элемент упорядоченной последовательности
- центральный элемент упорядоченной последовательности  . С помощью такого
. С помощью такого
фильтра выделяется маскирующая "точечная" (импульсная) помеха, когда за "точку" принимается любая пространственная композиция пикселей внутри "скользящего окна" суммарным размером ![]М*М/2[](/sites/default/files/tex_cache/cc5a2f6b93a10f9a5747d4e10219d38e.png) , обладающая максимальной или минимальной яркостью. Здесь
, обладающая максимальной или минимальной яркостью. Здесь ![]М*М/2[](/sites/default/files/tex_cache/cc5a2f6b93a10f9a5747d4e10219d38e.png) - младшее целое
- младшее целое  , а
, а  - нечетно. Такая "точечная" помеха способна в условиях активного противодействия противника сместить вычисленный "центр масс" факела за пределы угла обзора приемной ИК-камеры, что приведет к потере угловых координат самолета-лидера в ведомом беспилотном ЛА, то есть к разрыву сомкнутого строя и, как следствие, потери управления беспилотным ЛА.
- нечетно. Такая "точечная" помеха способна в условиях активного противодействия противника сместить вычисленный "центр масс" факела за пределы угла обзора приемной ИК-камеры, что приведет к потере угловых координат самолета-лидера в ведомом беспилотном ЛА, то есть к разрыву сомкнутого строя и, как следствие, потери управления беспилотным ЛА.
Алгоритмические затраты на вычисление каждого медианного значения  составляют
составляют  , если вычисление упорядочение (сортировку)
, если вычисление упорядочение (сортировку)  проводить методом "пузырька". Отсюда, общие алгоритмические затраты на медианную фильтрацию изображения
проводить методом "пузырька". Отсюда, общие алгоритмические затраты на медианную фильтрацию изображения  полутоновых черно-белых пикселей квадратично зависят от размеров обрабатываемого изображения
полутоновых черно-белых пикселей квадратично зависят от размеров обрабатываемого изображения  и биквадратно - от размеров "скользящего окна"
и биквадратно - от размеров "скользящего окна"  .
.
Именно биквадратная зависимость алгоритмических затрат вынуждает использовать векторно-конвейерную схему распараллеливания вычислений, которая обеспечивает согласование темпов реального времени между входными и обрабатываемыми потоками данных (рис. 4.18).
Действительно, если темп поступления пикселей составляет 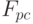 в секунду, то темп обработки должен составлять
в секунду, то темп обработки должен составлять  , так как вычисление медианы необходимо провести для каждого пикселя входного изображения, за исключением периферийных
, так как вычисление медианы необходимо провести для каждого пикселя входного изображения, за исключением периферийных  пикселей в каждой строке и в каждом столбце, для которых понятие медианы не определено (см.
рис. 4.17). Отсюда видно, что в системах реального времени коэффициент векторизации вычислительного алгоритма медианной фильтрации в принципе не может быть ниже площади "скользящего окна"
пикселей в каждой строке и в каждом столбце, для которых понятие медианы не определено (см.
рис. 4.17). Отсюда видно, что в системах реального времени коэффициент векторизации вычислительного алгоритма медианной фильтрации в принципе не может быть ниже площади "скользящего окна" 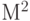 , и для его обеспечения блок медианной фильтрации, работающий по схеме
рис. 4.18, необходимо дополнить блоком векторизации
потока с одним входом и
, и для его обеспечения блок медианной фильтрации, работающий по схеме
рис. 4.18, необходимо дополнить блоком векторизации
потока с одним входом и 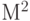 выходами (рис. 4.19).
выходами (рис. 4.19).
В схеме медианного фильтра
рис. 4.18 коэффициент векторно-конвейерного распараллеливания вычислений равен  , и в ней каждый узел должен выполнить (рис. 4.20) две операции: "сравнение" и "транспозиция" операндов по результату сравнения
, и в ней каждый узел должен выполнить (рис. 4.20) две операции: "сравнение" и "транспозиция" операндов по результату сравнения  .
.
Для значений яркости, укладывающихся в диапазон изменения 16-битных двоичных чисел, топологическая схема одного звена медианного фильтра (рис. 4.21) занимает бит-матрицу размером 6*7 бит-процессоров, и в ней:
- звено задержки, в данном случае на 27 тактов, реализовано на бит-процессорах (БП) первой строки матрицы, которые выполняют бит-операции
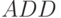 с дополнительной задержкой на 1 такт в канале АЛУ;
с дополнительной задержкой на 1 такт в канале АЛУ;
- блок сравнения, который выполняет сравнение двух чисел, заданных в формате фиксированной запятой со старшим буферным и следующим за ним знаковым разрядом
(
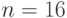 бит), выполнен на бит-процессорах матрицы с координатами (2,2)-(6,4);
бит), выполнен на бит-процессорах матрицы с координатами (2,2)-(6,4); - блок коммутации, который выполняет транспозицию входных операндов, выполнен на бит-процессорах матрицы с координатами (2,5)-(6,7).
В итоге для реализации медианного фильтра требуется бит-матрица размером не менее  бит-процессоров с временем задержки во всем тракте обработки порядка
бит-процессоров с временем задержки во всем тракте обработки порядка  , так как в конвей-ерной арифметике признак результата сравнения
, так как в конвей-ерной арифметике признак результата сравнения  вырабатывается с задержкой более чем
вырабатывается с задержкой более чем  тактов.
тактов.
Микропрограммный алгоритм процедуры сравнения двух операндов вытекает из традиционного правила:

которое в конвейерной арифметике реализуется следующим образом.
Шаг 1. Перевести операнд  из прямого кода в дополнительный код с принудительной инверсией знака и сохранением "нуля" в буферном разряде:
из прямого кода в дополнительный код с принудительной инверсией знака и сохранением "нуля" в буферном разряде:  ;
;  ,где
,где  - 16-битная циклическая константа вида
- 16-битная циклическая константа вида  , а
, а  - ее инверсия, которая поступает на вход
- ее инверсия, которая поступает на вход  на 1 такт раньше
на 1 такт раньше  .
.
Шаг 2. Сложить операнды и запомнить на  тактов знаковый разряд суммы:
тактов знаковый разряд суммы:  ;
;  где циклическая константа
где циклическая константа  подается на второй, управляющий вход
подается на второй, управляющий вход  с опережением на 2 такта по отношению к
с опережением на 2 такта по отношению к 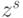 , которая поступает слева на первый, информационный вход этого БП (см.
табл. 5.8 курса "Задачи и модели вычислительных наноструктур").
, которая поступает слева на первый, информационный вход этого БП (см.
табл. 5.8 курса "Задачи и модели вычислительных наноструктур").
Блок коммутации реализует транспозицию входных операндов по правилу:

Таким образом:
- Показано, что технология микропрограммного конструирования МКМД-бит-потоковых субпроцессоров носит итерационный интерактивный характер и осуществляется "сверху-вниз" в структурно-функциональной плоскости проекта при декомпозиции задачи до микропрограммных процедур ее реализации и "снизу-вверх" в топологической плоскости проекта, которая и позволяет оценить реальные потребительские характеристики синтезируемого субпроцессора и закрепленного за ним БЭО.
- На основе топологической схемы микропрограммы можно получить все необходимые соотношения для вычисления потребительских характеристик МКМД-бит-потокового субпроцессора медианной фильтрации. В эти соотношения входят параметры обрабатываемого изображения -
 пикселей, параметры "скользящего окна" -
пикселей, параметры "скользящего окна" -  пикселей, темп поступления данных -
пикселей, темп поступления данных - 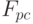 , зависящий от частоты кадров
, зависящий от частоты кадров  , а также параметры самой бит-матрицы: ее размеры и частота работы
(
, а также параметры самой бит-матрицы: ее размеры и частота работы
( 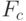 ), которая должна удовлетворять неравенству
), которая должна удовлетворять неравенству  , где
, где  - разрядность значений яркости полутонового черно-белого изображения.
- разрядность значений яркости полутонового черно-белого изображения. - В частности, уже при
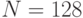 пикселей,
пикселей,  пикселей, частоте кадров
пикселей, частоте кадров 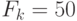 Гц и разрядности входных данных
Гц и разрядности входных данных  бит МКМД-бит-потоковый субпроцессор медианной фильтрации для поддержания темпа реального времени должен обеспечить пропускную способность:
бит МКМД-бит-потоковый субпроцессор медианной фильтрации для поддержания темпа реального времени должен обеспечить пропускную способность:- по потоку инструкций
 ;
; - по потоку данных -
 .
.
- по потоку инструкций





