|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
Сборка и установка Intel® Integrated Performance Primitives. Использование библиотеки в среде Microsoft® Visual Studio
4.5. Запуск приложения и проверка корректности
Для проверки корректности реализации, разработанной на базе Intel® IPP, необходимо реализовать функцию сравнения цветов пикселей отфильтрованных изображений. По существу в функции необходимо выполнить проход по всем пикселям и сравнить значения по каждому из трех каналов. В результате формируется количество пикселей, в которых не совпали значения интенсивности хотя бы по одному каналу.
int compare(const Mat &srcImgOCV, const Mat &srcImgIPP)
{
int kPoints = 0;
int w = srcImgOCV.size().width,
h = srcImgOCV.size().height, i, j, idx;
for (i = 0; i < h; i++)
{
idx = 3 * i * w;
for (j = 0; j < w; j++, idx += 3)
{
if (srcImgOCV.data[idx] –
srcImgIPP.data[idx] != 0 ||
srcImgOCV.data[idx + 1] –
srcImgIPP.data[idx + 1] != 0 ||
srcImgOCV.data[idx + 2] –
srcImgIPP.data[idx + 2] != 0)
{
kPoints++;
}
}
}
return kPoints;
}
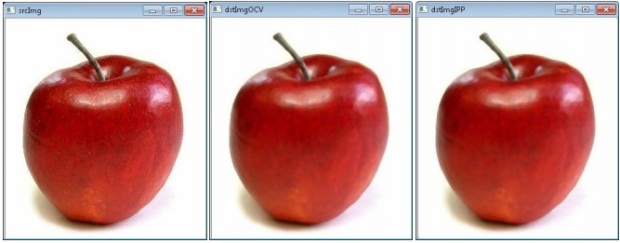
На данный момент можно выполнить запуск приложения, нажав сочетание клавиш Ctrl+F5. В результате работы программы будет показано три изображения: исходное и два отфильтрованных (рис. 10.11). Если приложение отработало корректно, то наряду с этим в консоли будет выведено соответствующее сообщение (рис. 10.12). В противном случае, в консоли появится сообщение об ошибке с указанием количества пикселей, в которых получены разные цвета.
5. Разработка приложения для поиска прямых линий на изображении с использованием Intel® Integrated Performance Primitives
5.1. Постановка задачи
Задача поиска заданных геометрических примитивов на изображении (прямых, эллипсов, окружностей и т.п.) – одна из актуальных задач компьютерного зрения. Данная задача возникает при разработке приложений в сфере робототехники и видеоаналитики в процессе поиска объектов, имеющих типичную геометрическую форму. Также существует опыт применения методов поиска примитивов при распознавании рукописных текстов.
Обобщенное преобразование Хафа – наиболее известный метод определения положения геометрических примитивов заданной формы на изображении. В настоящей работе предлагается использовать данное преобразование применительно к задаче поиска прямых линий.
Во второй части лабораторной работы требуется разработать приложение, которое удовлетворяет следующим требованиям:
- Поддержка возможности поиска прямых линий с использованием преобразования Хафа, реализованного в библиотеке OpenCV.
- Поддержка поиска прямых линий с использованием преобразования Хафа и других необходимых функций библиотеки Intel® IPP.
- Отображение полученных прямых линий на исходном изображении.
5.2. Преобразование Хафа
Преобразование Хафа – метод обнаружения прямых и более сложных кривых на бинарных изображениях. Метод позволяет определить параметры семейства кривых и обеспечивает поиск на изображении множества кривых указанного семейства [1]. Первоначально метод был разработан применительно к поиску прямых линий, впоследствии был обобщен на произвольное семейство кривых, заданных параметрически.
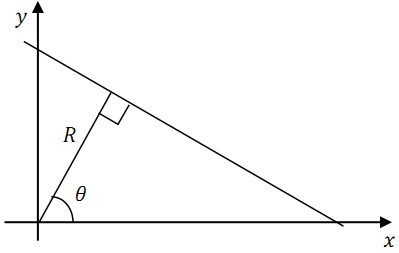
Рассмотрим схему работы преобразования Хафа для определения прямых линий на изображении [7]. Прямую на плоскости можно задать параметрически в виде (1), исходя из геометрического представления, показанного на рис. 10.13.
 |
( 1) |
где  – величина перпендикуляра, опущенного из начала координат системы
– величина перпендикуляра, опущенного из начала координат системы  на прямую,
на прямую,  – угол наклона перпендикуляра относительно оси
– угол наклона перпендикуляра относительно оси 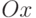 ,
, 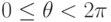 .
.
Тогда неявная функция, определяющая семейство прямых, может быть записана в форме (2).
 |
( 2) |
Таким образом, через каждую точку  проходит несколько прямых, соответствующих разным значениям параметров
проходит несколько прямых, соответствующих разным значениям параметров  и
и  . По существу любой фиксированной точке
. По существу любой фиксированной точке 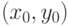 ставится в соответствие набор точек в пространстве параметров
ставится в соответствие набор точек в пространстве параметров 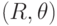 . В свою очередь каждой точке
. В свою очередь каждой точке 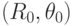 можно поставить в соответствие количество точек
можно поставить в соответствие количество точек  , лежащих на прямой
, лежащих на прямой  . Дискретность представления данных в машине требует введения сетки на плоскости параметров
. Дискретность представления данных в машине требует введения сетки на плоскости параметров 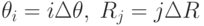 . И теперь каждой точке
. И теперь каждой точке 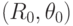 будем ставить в соответствие количество точек, принадлежащих семейству прямых (3).
будем ставить в соответствие количество точек, принадлежащих семейству прямых (3).
 |
( 3) |
Выбрав ячейку сетки, которой соответствует максимальное количество точек, получим наиболее вероятную прямую. В качестве параметров этой прямой можно принять координаты центра ячейки сетки. Если необходимо выделить несколько прямых, то достаточно отсортировать множество ячеек сетки в порядке убывания числа точек и выбрать определенное количество первых ячеек.