|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
Базовые операции обработки изображений
2.5. Оператор Лапласа
Математически оператор Лапласа представляет сумму квадратов вторых частных производных функции 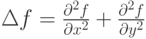 . Дискретный аналог оператора Лапласа используется при обработке изображений, в частности, для определения ребер объектов на изображении. Ребра формируются из множества пикселей, в которых оператор Лапласа принимает нулевые значения, т.к. нули вторых производных функции соответствуют экстремальным перепадам интенсивности.
. Дискретный аналог оператора Лапласа используется при обработке изображений, в частности, для определения ребер объектов на изображении. Ребра формируются из множества пикселей, в которых оператор Лапласа принимает нулевые значения, т.к. нули вторых производных функции соответствуют экстремальным перепадам интенсивности.
Библиотека OpenCV содержит функцию Laplacian, обеспечивающую вычисление оператора Лапласа [7].
void Laplacian(const Mat& src, Mat& dst, int ddepth,
int ksize=1, double scale=1, double delta=0,
int borderType=BORDER_DEFAULT)
Параметры функции:
- src, dst, ddepth, scale, delta, borderType имеют тот же смысл, что и при вызове функции Sobel.
-
kSize – размер апертуры для вычисление второй производной, является положительным четным числом. При использовании значения по умолчанию kSize=1 применяется апертура размером 3x3 и ядро представляется матрицей:

Приведем пример программы, которая обеспечивает поиск ребер объектов на изображения с помощью оператора Лапласа. Перед непосредственным применением оператора выполняется сглаживание с использованием фильтра Гаусса (GaussianBlur) и преобразование исходного изображения в оттенки серого (cvtColor). Заметим, что результирующие значения оператора Лапласа записываются в матрицу, глубина которой аналогично примеру с фильтром Собеля отличается от глубины исходного изображения, поэтому перед отображением выполняется преобразование полученной матрицы в 8-битную целочисленную посредством вызова функции convertScaleAbs.
#include <stdio.h>
#include <opencv2/opencv.hpp>
using namespace cv;
const char helper[] =
$quot;Sample_Laplacian.exe <img_file>\n\
\t<img_file> - image file name\n$quot;;
int main(int argc, char* argv[])
{
const char *initialWinName = $quot;Initial Image$quot;,
*laplacianWinName = $quot;Laplacian$quot;;
Mat img, grayImg, laplacianImg, laplacianImgAbs;
int ddepth = CV_16S;
if (argc < 2)
{
printf($quot;%s$quot;, helper);
return 1;
}
// загрузка изображения
img = imread(argv[1], 1);
// сглаживание с помощью фильтра Гаусса
GaussianBlur(img, img, Size(3,3),
0, 0, BORDER_DEFAULT);
// преобразование в оттенки серого
cvtColor(img, grayImg, CV_RGB2GRAY);
// применение оператора Лапласа
Laplacian(grayImg, laplacianImg, ddepth);
convertScaleAbs(laplacianImg, laplacianImgAbs);
// отображение результата
namedWindow(initialWinName, CV_WINDOW_AUTOSIZE);
namedWindow(laplacianWinName, CV_WINDOW_AUTOSIZE);
imshow(initialWinName, img);
imshow(laplacianWinName, laplacianImgAbs);
waitKey();
// закрытие окон
destroyAllWindows();
// осовобождение памяти
img.release();
grayImg.release();
laplacianImg.release();
laplacianImgAbs.release();
return 0;
}
Далее показан результат выделения ребер с использованием оператора Лапласа (рис. 7.8) на тестовом изображении, показанном ранее (рис. 7.2, слева).
2.6. Детектор ребер Канни
Детектор ребер Канни [4, 8, 9] предназначен для поиска границ объектов на изображении. Детектор строится на основании оператора Собеля и включает несколько этапов:
- Удаление шума на изображении посредством применения фильтра Гаусса с ядром размера 5:
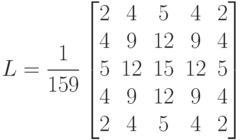
- Вычисление первых производных (магнитуд и направлений) функции интенсивности пикселей по горизонтальному и вертикальному направлениям посредством применения оператора Собеля с ядрами
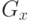 и
и 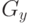 (см. раздел 2.4). Направления градиентов округляются до одного из возможных значений
(см. раздел 2.4). Направления градиентов округляются до одного из возможных значений 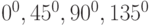 .
. - Отбор пикселей, которые потенциально принадлежат ребру с использованием процедуры non-maximum suppression [4]. Пиксели, которым соответствуют вектора производных по направлениям, являющиеся локальными максимумами, считаются потенциальными кандидатами на принадлежность ребру.
- Двойное отсечение (гистерезис). Выделяются "сильные" и "слабые" ребра. Пиксели, интенсивность которых превышает максимальный порог, считаются пикселями, принадлежащими "сильным" ребрам. Принимается, что пиксели с интенсивностью, входящей в интервал от минимального до максимального порогового значения, принадлежат "слабым" ребрам. Пиксели, интенсивность которых меньше минимального порога, отбрасываются из дальнейшего рассмотрения. Результирующие ребра содержат пиксели всех "сильных" ребер и те пиксели "слабых" ребер, чья окрестность содержит хотя бы один пиксель "сильных" ребер.
Детектор Канни реализован в библиотеке OpenCV [7] в виде отдельной функции, прототип которой приведен далее.
void Canny(const Mat& image, Mat& edges, double threshold1,
double threshold2, int apertureSize=3,
bool L2gradient=false)
Функция принимает на вход следующие параметры:
- image – одноканальное 8-битное изображение.
- edges – результирующая карта ребер, представляется матрицей, размер которой совпадает с размером исходного изображения.
- threshold1, threshold2 – параметры алгоритма, пороговые значения для отсечения.
- apertureSize – размер апертуры для применения оператора Собеля.
-
L2gradient – флаг, который указывает, по какой норме будет вычисляться магнитуда градиента. Принимает истинное значение, если используется норма
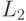 (корень квадратный из суммы квадратов частных производных), в противном случае
(корень квадратный из суммы квадратов частных производных), в противном случае 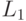 (сумма модулей частных производных). Как правило, нормы
(сумма модулей частных производных). Как правило, нормы 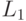 достаточно, и вычисляется она быстрее в связи с отсутствием вызова функции sqrt.
достаточно, и вычисляется она быстрее в связи с отсутствием вызова функции sqrt.
Приведем пример использования детектора Канни. Отметим, что перед непосредственным применением детектора выполняется размытие изображения (blur) и преобразование в оттенки серого (cvtColor).
#include <stdio.h>
#include <opencv2/opencv.hpp>
using namespace cv;
const char helper[] =
$quot;Sample_Canny.exe <img_file>\n\
\t<img_file> - image file name\n$quot;;
int main(int argc, char* argv[])
{
const char *cannyWinName = $quot;Canny detector$quot;;
Mat img, grayImg, edgesImg;
double lowThreshold = 70, uppThreshold = 260;
if (argc < 2)
{
printf($quot;%s$quot;, helper);
return 1;
}
// загрузка изображения
img = imread(argv[1], 1);
// удаление шумов
blur(img, img, Size(3,3));
// преобразование в оттенки серого
cvtColor(img, grayImg, CV_RGB2GRAY);
// применение детектора Канни
Canny(grayImg, edgesImg, lowThreshold, uppThreshold);
// отображение результата
namedWindow(cannyWinName, CV_WINDOW_AUTOSIZE);
imshow(cannyWinName, edgesImg);
waitKey();
// закрытие окон
destroyAllWindows();
// осовобождение памяти
img.release();
grayImg.release();
edgesImg.release();
return 0;
}
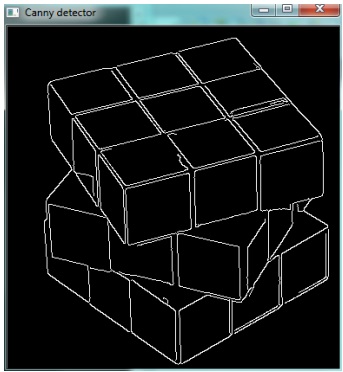
На рисунке (рис. 7.9) показан результат применения детектора Канни к тестовому изображению (рис. 7.2, слева).