| Россия |
Нейроподобные модели как формально-логический базис анализа живых систем
8.5. Фундаментальные константы как источник неоднозначной идентификации предметов и явлений природы
Относительные неудачи в создании промышленных нанотехнологий ставят вопрос о временном или фундаментальном характере связанных с ними проблем, из которых главная связана с необходимостью сохранения когерентных соотношений в квантовом "рабочем теле" на интервалах времени, характеризуемых как "техническая бесконечность".
Именно декогерентизация квантовых систем является главным источником потери однозначности, а значит, и управляемости извне, соотношений типа "вход-выход", без чего в принципе невозможно организовать вычислительный процесс. Поэтому имеет смысл проанализировать всевозможные источники неоднозначностей на всех уровнях организации вычислений.
Проблема измерения фундаментальных свойств молекулярно-биологических и физиологических систем (активность, целенаправленность, биологическая значимость и т. п.) стала камнем преткновения на пути широкомасштабного использования формальных моделей при описании живых систем [2, 17, 240, 241]. При этом упускался из виду тот факт, что только модели непрерывной математики требуют предварительных эмпирических измерений характеристик и свойств моделируемых процессов [242]. Но в математике исследуются не только численные соотношения, но и отношения, которые выражают связь (реальную или мнимую) между элементами некоторого множества [121]. Отношение не является операцией (функцией), и его конструктивное использование в моделях эмпирических систем не требует привлечения методов и средств непрерывной математики, которая и создавалась для нужд измерений различных величин: расстояние, площадь, объем, вес, скорость и так далее [243].
С этих позиций обращают на себя внимание два обстоятельства:
- Базовые закономерности (само)организации и развития предбиоло-гических, молекулярно-биологических и физиологических систем сложились в природе задолго до того, как человек стал пользоваться понятием "число" [244]. Это говорит не только о возможности, но и о достаточности представления таких закономерностей "нечисленными" формальными моделями, в основе которых лежит отношение "больше-меньше". Главное преимущество "нечисленной" формализации реального процесса: для нее требуется простейшая измерительная система типа рычажных весов, которая выполняет тривиальное эмпирическое сравнение.
- Физики давно преодолели примат числа и непрерывной величины, связав фундаментальные свойства релятивистских и квантовых систем с различными видами симметрии [96], для описания которой нет необходимости привлекать численные закономерности и достаточно использовать аппарат теории групп [103, 121].
Тем не менее, до сих пор принято считать, что измерительная система в виде аналитических весов более конструктивна, так как дает однозначный результат (в пределах погрешности измерений), в то время как измерительная система типа рычажных весов достаточно "грубая" и дает существенно неоднозначный результат измерений.
Покажем, что свойственная "нечисленным" методам неоднозначность идентификации в равной степени присуща и численным методам, так как в природе невозможно однозначно идентифицировать интересующие нас предметы и явления даже с привлечением фундаментальных физико-химических и молекулярно-биологических констант.
Геометрические константы были использованы первыми [244] при построении формальных моделей. Они учитывали только соотношение пространственных форм реальных физических объектов: длина окружности и радиус - 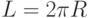 , площадь круга и квадрат радиуса -
, площадь круга и квадрат радиуса - 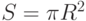 . Здесь
. Здесь  является безразмерным коэффициентом, и его можно представить в виде константы, задаваемой соотношением двух характеристик целого класса физических тел типа "круг", которое не зависит от индивидуальных размеров, каким бы способом ни проводились измерения пар
является безразмерным коэффициентом, и его можно представить в виде константы, задаваемой соотношением двух характеристик целого класса физических тел типа "круг", которое не зависит от индивидуальных размеров, каким бы способом ни проводились измерения пар 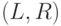 или
или 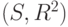 :
:  и
и  .
.
Определенная таким образом константа в скрытой форме уже содержит базовый для кибернетики принцип отрицательной обратной связи, который в данном случае говорит: любая непрерывная вариация числителя всегда компенсируется противоположной вариацией знаменателя. Поэтому справедливо обратное утверждение, которое составляет основу теории распознавания образов в кибернетике: все физические тела, в которых данные соотношения выполняются, можно идентифицировать как "круг", но с определенными оговорками:
-
 является иррациональным числом (несоизмеримым с единицей, по И. Ньютону [245]), и его вычисление на основе эмпирически измеренных пар
является иррациональным числом (несоизмеримым с единицей, по И. Ньютону [245]), и его вычисление на основе эмпирически измеренных пар 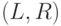 или
или 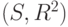 в общем случае представляет собой бесконечный процесс деления, то есть процесс идентификации по этому критерию не имеет строгого признака останова;
в общем случае представляет собой бесконечный процесс деления, то есть процесс идентификации по этому критерию не имеет строгого признака останова; - эмпирические пары, а с ними и вся измерительная система, должны быть определенного типа, который характеризуется единицами измерения, и поэтому из
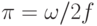 не следует, что идентифицирован объект типа "круг", так как здесь речь идет о частоте
не следует, что идентифицирован объект типа "круг", так как здесь речь идет о частоте  и круговой частоте
и круговой частоте  , которые с линейными размерами "круга" имеют мало общего.
, которые с линейными размерами "круга" имеют мало общего.
Отсюда, однозначно идентифицировать физический объект "круг" с помощью фундаментальной геометрической константы \pi невозможно, но благодаря этому его можно имитировать в частотной области, связанной с геометрическими параметрами имитируемого объекта только ассоциативно.
Физические константы трансформировались в ходе развития физических теорий: в классической механике - это коэффициенты пропорциональности, сопрягающие размерности величин, а в релятивистской и квантовой механике - это системообразующие инварианты.
В законе всемирного тяготения Ньютона 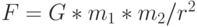 гравитационная постоянная
гравитационная постоянная 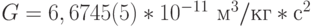 [97], как и
[97], как и  , выражается иррациональным числом, измеренным с ограниченной точностью. Она является коэффициентом пропорциональности, который сопрягает единицы измерения силы
, выражается иррациональным числом, измеренным с ограниченной точностью. Она является коэффициентом пропорциональности, который сопрягает единицы измерения силы  в левой части и произведения масс двух тел
в левой части и произведения масс двух тел  и
и 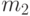 , деленной на квадрат расстояния между ними
, деленной на квадрат расстояния между ними 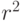 в правой части выражения. В классической кибернетической формулировке закон всемирного тяготения можно записать
в правой части выражения. В классической кибернетической формулировке закон всемирного тяготения можно записать  , где
, где  уже рассматривается как инварианта [14], которой можно идентифицировать физический объект "гравитационное поле". Здесь также требуется оговорка: такая идентификация справедлива только по Ньютону, так как, согласно принципу эквивалентности Эйнштейна, силы инерции, действующие в космическом корабле, "…летящем с ускорением, равным ускорению свободного падения у поверхности Земли, неотличимы от сил гравитации, действующих в истинном поле тяготения в корабле, стоящем на поверхности Земли " [97].
уже рассматривается как инварианта [14], которой можно идентифицировать физический объект "гравитационное поле". Здесь также требуется оговорка: такая идентификация справедлива только по Ньютону, так как, согласно принципу эквивалентности Эйнштейна, силы инерции, действующие в космическом корабле, "…летящем с ускорением, равным ускорению свободного падения у поверхности Земли, неотличимы от сил гравитации, действующих в истинном поле тяготения в корабле, стоящем на поверхности Земли " [97].
Таким образом, как и в случае с физическим объектом "круг", однозначно идентифицировать физический объект "гравитационное поле" с помощью фундаментальной константы всемирного тяготения невозможно чисто методически, но благодаря этому его можно имитировать с помощью ускоренных систем координат.
Во втором законе Ньютона 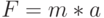 инерционная масса
инерционная масса  не является фундаментальной физической константой и используется как коэффициент пропорциональности, сопрягающий размерности силы
не является фундаментальной физической константой и используется как коэффициент пропорциональности, сопрягающий размерности силы  в левой части и ускорения
в левой части и ускорения  в правой части выражения. Тем не менее, в механике Ньютона в рамках конкретного физического эксперимента
в правой части выражения. Тем не менее, в механике Ньютона в рамках конкретного физического эксперимента  , что позволяет не только идентифицировать, но и сепарировать произвольные физические объекты по их массе
, что позволяет не только идентифицировать, но и сепарировать произвольные физические объекты по их массе  , проведя измерение
, проведя измерение  и
и  только в начале и в конце движения и исключив непрерывный контроль на всем пути.
только в начале и в конце движения и исключив непрерывный контроль на всем пути.
В специальной теории относительности А. Эйнштейна масса уже не является константой даже в рамках одного эксперимента и растет вместе со скоростью движения физического тела  :
:  . Здесь
. Здесь  - масса покоя, а
- масса покоя, а  [97] - скорость света в вакууме, которая является фундаментальной константой в рамках этой теории. Поэтому для идентификации "релятивистских" физических объектов можно использовать выражение, связывающее массу и энергию:
[97] - скорость света в вакууме, которая является фундаментальной константой в рамках этой теории. Поэтому для идентификации "релятивистских" физических объектов можно использовать выражение, связывающее массу и энергию: 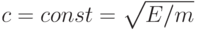 , которое говорит о том, что и данная фундаментальная константа является иррациональным числом, "измеренным" с конечной точностью.
, которое говорит о том, что и данная фундаментальная константа является иррациональным числом, "измеренным" с конечной точностью.
Инвариантность, а значит, и симметрия законов природы относительно некоторых преобразований составляет основу любой научной теории. В частности, в основе теории относительности лежит постулат инвариантности всего материального преобразованиям движения:
"… если преобразованию движения подвергнуть систему движущихся тел, то все относительные движения этих тел остаются неизменными" [97]. Кроме этого в специальной теории относительности сохраняется инвариантность законов природы следующим преобразованиям: перенос в пространстве, что говорит о равноправии всех точек пространства, то есть о его однородности; вращение в пространстве, что говорит о равноправии всех направлений в пространстве; сдвиг во времени, что говорит об однородности времени. Все четыре типа преобразований являются преобразованиями симметрии, а переносы и вращения в пространстве составляют предмет евклидовой геометрии, которая рассматривает физические тела в трехмерном пространстве. При скоростях, близких к скоростям света, евклидовы преобразования переноса и вращения с одной стороны и преобразования сдвига во времени и движения с другой стороны ненезависимы, что является следствием конечности фундаментальной константы c. В результате все четыре преобразования в теории относительности рассматриваются совместно в рамках геометрии "пространство - время" (пространственно-временной континуум). Таким образом, константа скорости света в вакууме является системообразующей в специальной теории относительности А. Эйнштейна, а субъект, отражающий "релятивистскую" внешнюю среду, должен уметь ее имитировать доступными ему неразличимыми эквивалентами.
Универсальная мировая постоянная Планка  [97]
[97]  ) выражается иррациональным числом, имеет размерность действия, называется квантом действия и является фундаментальной в нерелятивистской квантовой механике, так как:
) выражается иррациональным числом, имеет размерность действия, называется квантом действия и является фундаментальной в нерелятивистской квантовой механике, так как:
- ограничивает область применения классической механики размерностью действий, которые должны намного превосходить по величине
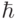 ;
; - сопрягает размерности в дуальном соотношении
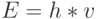 , где энергия
, где энергия  характеризует поведение частицы, а частота
характеризует поведение частицы, а частота  - поведение волны;
- поведение волны; - задает порог минимально достижимой неоднозначности одновременного измерения координаты и импульса элементарной частицы, который, согласно принципу неопределенности Гейзенберга, определяется соотношением
 , где две неопределенности
, где две неопределенности  и
и 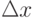 представляют собой среднеквадратичное отклонение соответственно импульса и координаты от их среднего значения.
представляют собой среднеквадратичное отклонение соответственно импульса и координаты от их среднего значения.
С позиций кибернетики постоянная Планка позволяет:
- с помощью
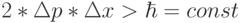 идентифицировать и отделить квантовые физические объекты от "неквантовых";
идентифицировать и отделить квантовые физические объекты от "неквантовых"; - с помощью
 идентифицировать и имитировать частицы методами и средствами измерения непрерывных волновых процессов и, наоборот, волновые процессы - методами и средствами измерения корпускулярных процессов.
идентифицировать и имитировать частицы методами и средствами измерения непрерывных волновых процессов и, наоборот, волновые процессы - методами и средствами измерения корпускулярных процессов.
Отсюда, в классе квантовых объектов и систем имеется два источника неоднозначной идентификации, один из которых связан с принципом неопределенности Гейзенберга, а второй - с их двойственной природой, причем постоянная Планка входит в оба выражения, задающие численное соотношение между неоднозначно измеряемыми свойствами квантовых объектов.
Приведенные данные позволяют утверждать:
- для идентификации физического объекта или системы необходимо измерить как минимум два свойства и вычислить инварианту, которая определяется численным соотношением измеренных свойств;
- главными источниками неоднозначной идентификации физических объектов являются три типа погрешностей: методическая, определяемая естественным дуализмом идентифицируемых объектов, измерения фундаментальных свойств и вычисления фундаментальных констант, которые являются иррациональными числами;
- инвариантность фундаментальных физических констант предполагает вариационный и, как правило, непрерывный характер измерения базовых свойств физического объекта, которые можно провести объективно, то есть в широком комплексе изменения измеряемых свойств и внешних условий, или субъективно и даже волюнтаристски, то есть на основе одного измерения и при неизвестном комплексе внешних условий;
- неоднозначность идентификации физических объектов является главным источником их адекватной имитации в конкретном комплексе внешних и внутренних условий.
Химические константы связаны с превращениями молекул, которые обмениваются атомами друг с другом, распадаются на молекулы с меньшим числом атомов или образуют новые вещества [246]. Химические превращения реализуются через макроскопические взаимодействия множественных совокупностей атомов. Такие взаимодействия в первую очередь зависят от количественного и качественного состава атомов, температуры, давления, степени замкнутости системы по потокам массы и энергии и т. п. Поведение неоднородных, массовых совокупностей "элементарных" физических объектов удается описать математически только с помощью усредненных статистических характеристик, которые нивелируют особенности поведения каждого члена совокупности [97, 246]:
- Газовая постоянная
 входит в уравнение состояния 1 моля идеального газа
входит в уравнение состояния 1 моля идеального газа 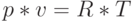 и по своему физическому смыслу является работой по расширению 1 моля идеального газа под постоянным давлением при нагревании на 1 градус Кельвина (К). Здесь
и по своему физическому смыслу является работой по расширению 1 моля идеального газа под постоянным давлением при нагревании на 1 градус Кельвина (К). Здесь  - давление,
- давление,  - объем моля,
- объем моля,  - абсолютная температура.
- абсолютная температура. - Постоянная Больцмана
 , которая связывает энтропию
, которая связывает энтропию  физической системы с вероятностью осуществления в ней макроскопического состояния
физической системы с вероятностью осуществления в ней макроскопического состояния 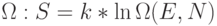 , где
, где  - число Авогадро, которое харак-теризует число структурных элементов (атомов, молекул, ионов) в единице количества вещества 1 моль,
- число Авогадро, которое харак-теризует число структурных элементов (атомов, молекул, ионов) в единице количества вещества 1 моль,  - число квантовых уровней в узком интервале энергии
- число квантовых уровней в узком интервале энергии 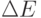 вблизи значения энергии
вблизи значения энергии  системы из
системы из  частиц.
частиц.
Обе фундаментальные химические константы сохраняют все атрибуты физических констант: они выражаются иррациональными числами, а для идентификации с их помощью замкнутых систем необходимо измерить не менее двух макроскопических величин и проконтролировать условие 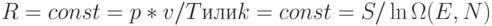 , так как, согласно Больцману, энтропия
, так как, согласно Больцману, энтропия  замкнутой системы возрастает, что обусловлено ее переходом из менее вероятного состояния в более вероятное.
замкнутой системы возрастает, что обусловлено ее переходом из менее вероятного состояния в более вероятное.
Формулируя предмет кибернетики [14], Н. Винер обратил внимание на тот факт, что к статистическим моделям ньютоновских систем пришлось прибегнуть из-за невозможности определить начальные скорости и импульсы составляющих элементов. В частности, распределение по скоростям частиц макроскопической физической системы, находящейся в статистическом равновесии, при условии, что движение этих частиц подчинено законам классической механики, определяется соотношением Максвелла [97]:
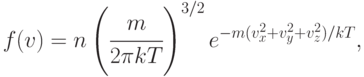
где 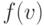 - вероятное число молекул в единичном объеме, компоненты скоростей которых лежат в интервалах от
- вероятное число молекул в единичном объеме, компоненты скоростей которых лежат в интервалах от  до
до 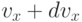 , от
, от 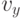 до
до 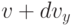 и от
и от 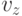 до
до 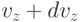 , а
, а  и
и  - соответственно масса молекул и их количество в единице объема.
- соответственно масса молекул и их количество в единице объема.
Распределение Максвелла является частным случаем канонического распределения Гиббса, и оба включают постоянную Больцмана в качестве константы. Каноническое распределение Гиббса характеризует распределение вероятностей состояний статистического ансамбля, который находится в тепловом равновесии со средой и может обмениваться с ней энергией при постоянном объеме и постоянном числе частиц [97]:
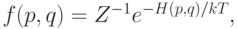
где 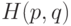 - гамильтониан функции системы,
- гамильтониан функции системы, 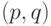 - обобщенные координаты и импульсы всех частиц системы соответственно, а
- обобщенные координаты и импульсы всех частиц системы соответственно, а
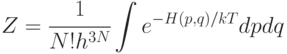
статистический интеграл, определяемый из условия нормировки функции 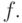 Отсюда, идентифицировать, а значит, и контролировать состояние равновесия химической реакции
Отсюда, идентифицировать, а значит, и контролировать состояние равновесия химической реакции
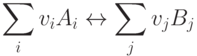
статистическими методами достаточно накладно. Поэтому в химии для этих целей используют константу равновесия:
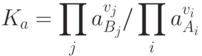
которая задает соотношение между активностями 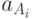 реагирующих веществ
реагирующих веществ 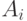 и активностями
и активностями 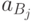 продуктов реакции
продуктов реакции 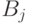 . Здесь
. Здесь 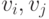 - стехиометрические коэффициенты, выражающие соотношение между количествами молей реагентов и продуктов реакции. При этом между константами равновесия и статистическими характеристиками реакции нет однозначного соответствия, так как они связаны между собой стандартным изменением энергии Гиббса
- стехиометрические коэффициенты, выражающие соотношение между количествами молей реагентов и продуктов реакции. При этом между константами равновесия и статистическими характеристиками реакции нет однозначного соответствия, так как они связаны между собой стандартным изменением энергии Гиббса 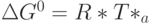 , которое зависит от выбора стандартного состояния для реагирующих веществ и продуктов реакции.
, которое зависит от выбора стандартного состояния для реагирующих веществ и продуктов реакции.
Но в природе кроме равновесных систем существуют еще и неравновесные, поведение которых исследуется и описывается методами и средствами термодинамики необратимых процессов. Если для равновесных (обратимых) процессов удается найти их полное количественное описание, то для неравновесных (необратимых) процессов можно установить только количественные неравенства, которые указывают возможные направления течения этих процессов. Для неравновесных систем справедливы обобщенные законы сохранения массы, импульса и энергии, но энтропия таких систем не сохраняется, а возрастает во времени благодаря необратимости протекающих процессов. В этом случае производство энтропии определяется соотношением  , где суммирование ведется по
, где суммирование ведется по 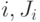 - тепловые, диффузионные и т. п. потоки, а
- тепловые, диффузионные и т. п. потоки, а 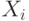 - сопряженные им термодинамические силы, то есть градиенты термодинамических параметров, приводящие к отклонению от равновесия. В неравновесных системах при малых отклонениях от термодинамического равновесия возникающие потоки линейно зависят от термодинамических сил:
- сопряженные им термодинамические силы, то есть градиенты термодинамических параметров, приводящие к отклонению от равновесия. В неравновесных системах при малых отклонениях от термодинамического равновесия возникающие потоки линейно зависят от термодинамических сил: 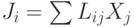 , где суммирование ведется по
, где суммирование ведется по  , а
, а  - феноменологические коэффициенты или коэффициенты переноса. В результате термодинамическая сила
- феноменологические коэффициенты или коэффициенты переноса. В результате термодинамическая сила  вызывает соответствующий ей поток
вызывает соответствующий ей поток 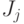 , то есть градиент температуры вызывает поток теплоты (теплопроводность), градиент концентрации - поток вещества (диффузия), градиент скорости - поток импульса (определяет вязкость) и т. п.
, то есть градиент температуры вызывает поток теплоты (теплопроводность), градиент концентрации - поток вещества (диффузия), градиент скорости - поток импульса (определяет вязкость) и т. п.
Однако одних количественных, в том числе и статистических показателей явно недостаточно для адекватного представления химических превращений. В частности, изомеры статистически неразличимы, так как имеют одинаковый состав и молекулярную массу. Тем не менее, они разнятся свойствами, что обусловлено различным строением и пространственным расположением атомов. В химии отличают структурную и пространственную изомерию [246], первая из которых подразделяется на изомерию скелета, обусловленную различным порядком связи атомов, образующих скелет молекулы, и изомерию положения, обусловленную различным расположением функциональных групп при фиксированном скелете молекул. Стереоизомеры имеют одинаковый порядок связей атомов, но отличаются их расположением в пространстве [246]: оптические (обусловлены хираль-ностью элементов молекулы), геометрические (свойственны соединениям с двойными связями и малыми циклами) и конформационные (обусловлены существованием в молекуле нескольких конформаций).
Изомеры могут превращаться друг в друга с образованием подвижного равновесного состояния (таутомерия), то есть существует целый класс химических превращений, который не выводит нас за рамки преобразований отношения структурного или пространственного порядка. Это говорит о том, что математические модели реальных объектов и процессов можно строить не только на основе преобразований, сохраняющих меру, которые составляют основу кибернетики Н. Винера, но и на основе преобразований, сохраняющих некоторое отношение. При этом необходимо учитывать, что классы преобразований, сохраняющих меру и сохраняющих отношение, пересекаются только частично, то есть существуют преобразования, сохраняющие меру, но не отношение, сохраняющие отношение, но не меру, и сохраняющие как меру, так и отношение.
В частности:
- любые деформации круга, преобразующие его в эллипс, сохраняют площадь (меру), но нарушают линейные отношения между длиной окружности (периметром) и радиусом;
- при игре на баяне или аккордеоне отношение порядка между мехами сохраняется, но длина инструмента (мера) непрерывно изменяется;
- из аддитивного свойства меры следует, что ее значение не зависит от порядка суммирования или интегрирования, то есть от порядка перечисления ее компонент.
Упорядоченность и связанное с ней отношение порядка играют ключевую роль в общей теории систем [247], так как количество информации, содержащейся в системе, служит мерой нашего знания правил, с помощью которых получена упорядоченность, характерная для данной системы. В частности, для передачи по каналу связи любого иррационального числа требуется количество бит информации, которое возрастает до бесконечности с ростом точности представления данного числа. Но можно передавать не само иррациональное число, а соотношение для его
вычисления, для чего требуется ограниченное количество бит. Поэтому в теории систем отличают структурную и функциональную упорядоченность. Первая обычно проявляется через некоторую регулярность, симметрию или повторяемость, и ее легко обнаружить, но достаточно трудно (громоздко) описать. Обнаружение второй требует более глубоких исследований, но когда найдена закономерность, лежащая в основе функциональной упорядоченности, исчезает и элемент неожиданности, а объем информации, необходимой для ее описания, резко падает, как это имеет место с константой равновесия.
Отсюда, центральная задача практически любого научного исследования состоит как минимум в раскрытии механизмов упорядочения эмпирической или формальной системы.
Предбиологические механизмы самоорганизации, понимаемой как пространственно-временная упорядоченность, были раскрыты с помощью термодинамики неравновесных систем, где всегда имеющие место конвективные потоки флуктуационного происхождения при определенных критических температурах могут усиливаться, что приводит к образованию макроскопических потоков, стабилизированных за счет обмена энергией с внешней средой [33, 34]. Такой механизм получил название "упорядочение через флуктуацию", а порождаемый им порядок - дис-сипативные структуры.
