|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Дележ, отвечающий аксиомам Нэша
Теорема 3.1. Существует единственная функция  из (14.18), определенная для всех задач о сделках,
задаваемых тройками (S,u*,v*) и удовлетворяющих
аксиомам (14.15)-(14.17), (14.19), (14.21), (14.22). При этом предполагается,
что хотя бы для одной пары (u,v) из замкнутого,
ограниченного и выпуклого множества S, входящего в определение задачи, справедливо (может быть
нестрогое) доминирование
из (14.18), определенная для всех задач о сделках,
задаваемых тройками (S,u*,v*) и удовлетворяющих
аксиомам (14.15)-(14.17), (14.19), (14.21), (14.22). При этом предполагается,
что хотя бы для одной пары (u,v) из замкнутого,
ограниченного и выпуклого множества S, входящего в определение задачи, справедливо (может быть
нестрогое) доминирование
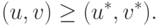 |
( 15.1) |
Доказательство теоремы опирается на следующие леммы.
Лемма 3.1. Если множество S содержит точку (u,v), такую, что
 |
( 15.2) |
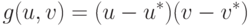 |
( 15.3) |
 |
( 15.4) |
 .
.Доказательство Поскольку функция (15.3) является непрерывной, а непустое множество (15.4) - ограниченным и замкнутым, то существует максимум
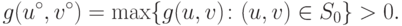 |
( 15.5) |
Допустим, что существует еще одна точка (u',v'), максимизирующая функцию g на S0. Тогда
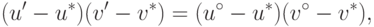 |
( 15.6) |
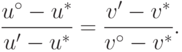
Поскольку точки  и
и 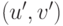 являются (по предположению) различными, то из (15.6) вытекают следствия:
являются (по предположению) различными, то из (15.6) вытекают следствия:
 |
( 15.7) |
Из выпуклости множества S0 следует справедливость включения
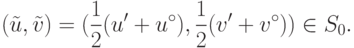
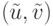 имеет место неравенство
имеет место неравенство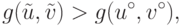 |
( 15.8) |
 из (15.5), что доказывает единственность точки максимума функции g.
Действительно,
из (15.5), что доказывает единственность точки максимума функции g.
Действительно,![\begin{gathered}
g(\tilde{u}, \tilde{v}) = \frac{1}{4}\left[(u' - u^\ast) +
(u^\circ - u^\ast)\right]\left[(v' - v^\ast) + (v^\circ -
v^\ast)\right]=\\ = \frac{1}{2}(u' - u^\ast)(v' - v^\ast) +
\frac{1}{2}(u^\circ -
u^\ast)(v^\circ - v^\ast) + \frac{1}{4}(u^\circ - u')(v' - v^\circ),
\end{gathered}](/sites/default/files/tex_cache/faf21a9fe868f92ddc21efc5d6e6dd27.png)
В дальнейшем мы покажем, что условия (15.5) определяют функцию  из (14.18),
и опишем графический прием для определения аргумента
из (14.18),
и опишем графический прием для определения аргумента  из левой части (15.5).
из левой части (15.5).
Лемма 3.2. Пусть выполняются условия (15.2) и точка  удовлетворяет
определению (15.5). Тогда множество
удовлетворяет
определению (15.5). Тогда множество  лежит под прямой линией, определяемой уравнением
лежит под прямой линией, определяемой уравнением
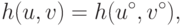 |
( 15.9) |
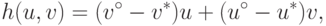 |
( 15.10) |
 , т.е.
, т.е.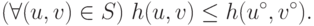
Доказательство. Допустим, что прямая (15.9)
не является опорной для множества S в точке  .
Тогда существует такая точка
.
Тогда существует такая точка 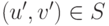 , что
, что
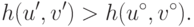 |
( 15.11) |
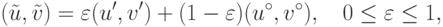
 в силу его выпуклости.
Поскольку
в силу его выпуклости.
Поскольку 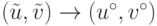 при
при 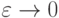 и, согласно правому неравенству
в (15.5),
и, согласно правому неравенству
в (15.5), 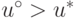 , то при достаточно малых значениях
, то при достаточно малых значениях 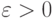 справедливо включение
справедливо включение 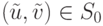 .
.Теперь покажем, что при достаточно малых значениях 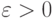 имеет место
неравенство
имеет место
неравенство 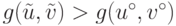 ,
противоречащее определению (15.5). Действительно,
,
противоречащее определению (15.5). Действительно,
![\begin{multiline*}
g(\tilde{u}, \tilde{v}) = [u^\circ + \varepsilon(u' - u^\circ) - u^\ast]
[v^\circ + \varepsilon(v' - v^\circ) - v^\ast]) =\\
= (u^\circ - u^\ast)(v^\circ - v^\ast) +
\varepsilon^2(u' - u^\circ)(v' - v^\circ) + \\
+\varepsilon[(v^\circ - v^\ast)
(u' - u^\circ) + (u^\circ - u^\ast)(v' - v^\circ)],
\end{multiline*}](/sites/default/files/tex_cache/4416884bab88fdde017ac932fdd7b604.png)
 является положительным, а член, содержащий
является положительным, а член, содержащий 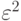 , -
пренебрежимо малым при
, -
пренебрежимо малым при 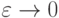 .
Следовательно, прямая линия (15.9)
является опорной к множеству S в точке
.
Следовательно, прямая линия (15.9)
является опорной к множеству S в точке  .
.
