|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Экспертные методы принятия решений
Таким образом, важна конкретная (узкая) постановка задачи перед экспертами. Но такой постановки зачастую нет. А тогда "игры" по разработке обобщенного показателя качества - например, в виде линейной функции от перечисленных переменных - не могут дать объективных выводов. Альтернативой единственному обобщенному показателю является математический аппарат типа многокритериальной оптимизации - множества Парето и т.д.
В некоторых случаях все-таки можно глобально сравнить объекты - например, с помощью тех же экспертов получить упорядочение рассматриваемых объектов - изделий или проектов. Тогда можно ПОДОБРАТЬ коэффициенты при отдельных показателях так, чтобы упорядочение с помощью линейной функции возможно точнее соответствовало глобальному упорядочению (например, найти эти коэффициенты методом наименьших квадратов). Наоборот, в подобных случаях НЕ СЛЕДУЕТ оценивать указанные коэффициенты с помощью экспертов. Эта простая идея до сих пор не стала очевидной для отдельных составителей методик по проведению экспертных опросов и анализу их результатов. Они упорно стараются заставить экспертов делать то, что они качественно выполнить не в состоянии - указывать веса, с которыми отдельные показатели качества должны входить в итоговый обобщенный показатель.
Эксперты обычно могут сравнить объекты или проекты в целом, но не могут вычленить вклад отдельных факторов. Раз организаторы опроса спрашивают, эксперты отвечают, но эти ответы не несут в себе надежной информации о реальности...
Число туров. Второе основание классификации экспертных процедур - число туров. Экспертизы могут включать один тур, некоторое фиксированное число туров (два, три,…) или неопределенное число туров. Чем больше туров, тем более тщательным является анализ ситуации, поскольку эксперты при этом обычно много раз возвращаются к рассмотрению предмета экспертизы. Но одновременно увеличивается общее время на экспертизу и возрастает ее стоимость. Можно уменьшить расходы, вводя в экспертизу не всех экспертов сразу, а постепенно. Так, например, если цель состоит в сборе аргументов "за" и "против", то первоначальный перечень аргументов может быть составлен одним экспертом. Второй добавит к нему свои аргументы. Суммарный материал поступит к первому и третьему, которые внесут свои аргументы и контраргументы. И так далее - добавляется по одному эксперту на каждый новый тур.
Наибольшие сложности вызывают процедуры с заранее неопределенным числом туров, например, "снежный ком". Часто задают максимально возможное число туров, и тогда неопределенность сводится к тому, придется ли проводить это максимальное число туров или удастся ограничиться меньшим числом.
Организация общения экспертов. Третье основание классификации экспертных процедур - способ организации общения экспертов. Рассмотрим достоинства и недостатки каждого из элементов шкалы: отсутствие общения - заочное анонимное общение - заочное общение без анонимности - очное общение с ограничениями - очное общение без ограничений.
При отсутствии общения эксперт высказывает свое мнение, ничего не зная о других экспертах и об их мнениях. Он полностью независим, что и хорошо, и плохо. Обычно такая ситуация соответствует однотуровой экспертизе.
Заочное анонимное общение, например, как в методе Дельфи, означает, что эксперт знакомится с мнениями и аргументами других экспертов, но не знает, кто именно высказал то или иное положение. Следовательно, в экспертизе должно быть предусмотрено хотя бы два тура.
Заочное общение без анонимности соответствует, например, общению по Интернету. Все варианты заочной экспертизы хороши тем, что нет необходимости собирать экспертов вместе, следовательно, находить для этого удобное время и место. В будущем с распространением телеконференций грань между очным и заочным общением экспертов начнет стираться.
При очных экспертизах эксперты говорят, а не пишут, как при заочных, и потому успевают за то же потраченное время сообщить существенно больше. Очная экспертиза с ограничениями весьма распространена. Это - собрание, идущее по фиксированному регламенту. Примером является военный совет в императорской русской армии, когда эксперты (офицеры и генералы) высказывались в фиксированном порядке от младшего (по чину и должности) к старшему. Другой пример - разработка и принятие решений в Государственной Думе Российской Федерации.
Наконец, очная экспертиза без ограничений - это свободная дискуссия.
Все очные экспертизы имеют недостатки, связанные с возможностями отрицательного влияния на их проведение социально-психологических свойств и клановых (партийных) пристрастий участников, а также неравенства их профессионального, должностного, научного статусов. Представьте себе, что соберутся вместе 5 лейтенантов и 3 генерала. Независимо от того, какая информация имеется у того или иного участника встречи, ход ее предсказать нетрудно: генералы будут беседовать, а лейтенанты - помалкивать. При этом вполне очевидно, что лейтенанты получили образование позже генералов, а потому обладают полезной информацией, которой нет у генералов.
Веса экспертов. Четвертое основание классификации экспертных процедур - по способам введения весов для мнений экспертов. Простейший способ - все эксперты равноправны, при голосованиях по отдельным положениям разрабатываемого решения имеют по одному голосу.
Часто вводят понятия решающего голоса и совещательного голоса. Например, при защите дипломного проекта члены Государственной Аттестационной Комиссии (ГАК) имеют решающие голоса, а все остальные участники заседания - совещательные. В Федеральном законе "Об экологической экспертизе" (1995) подробно расписано, представители каких организаций и структур управления могут присутствовать на заседании экспертной комиссии государственной экологической экспертизы с правом совещательного голоса.
В регламент принятия решений иногда включают положение, согласно которому при делении голосов ровно пополам принимается мнение той половины, к которой относится председатель ЭК. Это означает, что вес голоса председателя на бесконечно малую величину больше веса рядового эксперта.
При голосованиях на собраниях акционеров вес каждого эксперта (участника заседания) определяется числом акций, которыми он распоряжается.
Комбинация различных видов экспертизы. Реальные экспертизы часто представляют собой комбинации различных описанных выше типов экспертиз. В качестве примера рассмотрим защиту студентом дипломного проекта. Сначала идет многотуровая очная экспертиза, проводимая научным руководителем и консультантами, в результате студент подготавливает проект к защите. Затем два эксперта работают заочно - это автор отзыва сторонней организации и заведующий кафедрой, допускающий работу к защите. Обратите внимание на различие задач этих экспертов и объемов выполняемой ими работы - один пишет подробный отзыв, второй росписью на титульном листе проекта разрешает его защиту. Наконец - очная экспертиза без ограничений (для членов ГАК - государственной аттестационной комиссии). Дипломный проект оценивается коллегиально, по большинству голосов, при этом один из экспертов (научный руководитель) знает работу подробно, а остальные - в основном лишь по докладу. Отметим, что мнения экспертов учитываются с весами, а именно, мнения членов ГАК - с весом 1, мнения всех остальных - с весом 0 (совещательный голос). Таким образом, имеем сочетание многотуровой и однотуровой, заочных и очных экспертиз. Подобные сочетания характерны для многих реально проводящихся экспертиз.
Методы средних рангов
Современная теория измерений и экспертные оценки.Как проводить анализ собранных рабочей группой ответов экспертов? Для более углубленного рассмотрения проблем экспертных оценок понадобятся некоторые понятия теории измерений , служащей основой теории экспертных оценок, прежде всего той ее части, которая связана с анализом заключений экспертов, выраженных в качественном (а не в количественном) виде. Теория измерений интересует нас, в частности, в связи с агрегированием мнений экспертов, построением обобщенных показателей (их называют также рейтингами).
Получаемые от экспертов мнения часто выражены в порядковой шкале, т.е. эксперт может сказать (и обосновать), что один тип продукции будет более привлекателен для потребителей. Что один показатель качества продукции более важен, чем другой, первый технологический объект более опасен, чем второй, и т.д. Но он не в состоянии сказать, во сколько раз или на сколько более важен, соответственно, более опасен. Поэтому экспертов часто просят дать ранжировку (упорядочение) объектов экспертизы, т.е. расположить их в порядке возрастания (или, точнее, неубывания) интенсивности интересующей организаторов экспертизы характеристики.
Ранжировки определяются и изучаются с помощью рангов. Ранг - это номер (объекта экспертизы) в упорядоченном ряду. Формально ранги выражаются числами 1, 2, 3, ..., но весьма важно то, что с этими числами нельзя делать привычные арифметические операции. Например, хотя 1 + 2 = 3, но нельзя утверждать, что для объекта, стоящем на третьем месте в упорядочении (в другой терминологии - ранжировке), интенсивность изучаемой характеристики равна сумме интенсивностей объектов с рангами 1 и 2. Так, один из видов экспертного оценивания - оценки достижений спортсменов. Разве можно сказать, что спортсмен, занявший третье место, достиг того же, что и спортсмены, занявшие первое и второе места, вместе взятые? Поэтому очевидно, что для анализа подобного рода качественных данных необходима не обычная арифметика, а другая теория, дающая базу для разработки, изучения и применения конкретных методов расчета. Эта другая теория и есть теория измерений (ТИ).
Рассмотрим в качестве примера применения результатов ТИ, касающихся средних величин в порядковой шкале, один сюжет, связанный с ранжировками и рейтингами.
Сравнение на основе средних баллов. В настоящее время распространены экспертные, маркетинговые, квалиметрические, социологические и иные опросы, в которых используются балльные оценки. В таких исследованиях опрашиваемых просят выставить баллы объектам, изделиям, технологическим процессам, предприятиям, проектам. Или же заявкам на выполнение научно-исследовательских работ, идеям, проблемам, программам, политикам и т.п. Затем рассчитывают средние баллы и рассматривают их как интегральные (т.е. обобщенные, итоговые) оценки, выставленные объектам экспертизы коллективом опрошенных экспертов. Какими формулами пользоваться для вычисления средних величин? Ведь средних величин существует, как мы знаем, очень много разных видов.
Обычно применяют среднее арифметическое. Специалисты по теории измерений уже более 30 лет знают, что такой способ некорректен, поскольку баллы обычно измерены в порядковой шкале. Обоснованным является использование медиан в качестве средних баллов. Однако полностью игнорировать средние арифметические нецелесообразно из-за их привычности и распространенности. Поэтому представляется рациональным использовать одновременно оба метода - и метод средних арифметических рангов (баллов), и методов медианных рангов. Такая рекомендация находится в согласии с общенаучной концепцией устойчивости, рекомендующей применять различные методы для обработки одних и тех же данных с целью выделить выводы, получаемые одновременно при всех методах. Такие выводы, видимо, соответствуют реальной действительности, в то время как заключения, меняющиеся от метода к методу, зависят от субъективизма исследователя, выбирающего метод обработки исходных экспертных оценок.
Пример сравнения восьми проектов. Рассмотрим конкретный пример применения только что сформулированного подхода.
По заданию руководства фирмы анализировались восемь проектов, предлагаемых для включения в план стратегического развития фирмы. Они обозначены следующим образом: Д, Л, М-К, Б, Г-Б, Сол, Стеф, К (по фамилиям менеджеров, предложивших их для рассмотрения). Все проекты были направлены 12 экспертам, включенным в экспертную комиссию, организованную по решению Правления фирмы. В приведенной ниже табл. 11.1 приведены ранги восьми проектов, присвоенные им каждым из 12 экспертов.
Ранги присваивались в соответствии с представлениями экспертов о целесообразности включения проектов в стратегический план фирмы. При этом эксперт присваивает ранг 1 самому лучшему проекту, который обязательно надо реализовать. Ранг 2 получает от эксперта второй по привлекательности проект, ..., наконец, ранг 8 - наиболее сомнительный проект, который реализовывать стоит лишь в последнюю очередь.
| № эксперта | Д | Л | М-К | Б | Г-Б | Сол | Стеф | К |
|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 3 | 1 | 2 | 8 | 4 | 6 | 7 |
| 2 | 5 | 4 | 3 | 1 | 8 | 2 | 6 | 7 |
| 3 | 1 | 7 | 5 | 4 | 8 | 2 | 3 | 6 |
| 4 | 6 | 4 | 2,5 | 2,5 | 8 | 1 | 7 | 5 |
| 5 | 8 | 2 | 4 | 6 | 3 | 5 | 1 | 7 |
| 6 | 5 | 6 | 4 | 3 | 2 | 1 | 7 | 8 |
| 7 | 6 | 1 | 2 | 3 | 5 | 4 | 8 | 7 |
| 8 | 5 | 1 | 3 | 2 | 7 | 4 | 6 | 8 |
| 9 | 6 | 1 | 3 | 2 | 5 | 4 | 7 | 8 |
| 10 | 5 | 3 | 2 | 1 | 8 | 4 | 6 | 7 |
| 11 | 7 | 1 | 3 | 2 | 6 | 4 | 5 | 8 |
| 12 | 1 | 6 | 5 | 3 | 8 | 4 | 2 | 7 |
Примечание.Эксперт № 4 считает, что проекты М-К и Б равноценны, но уступают лишь одному проекту - проекту Сол. Поэтому проекты М-К и Б должны были бы стоять на втором и третьем местах и получить баллы 2 и 3. Поскольку они равноценны, то получают средний балл 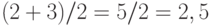 .
.
Анализируя результаты работы экспертов (т.е. упомянутую таблицу), члены аналитического подразделения Рабочей группы, анализировавшие ответы экспертов по заданию Правления фирмы, были вынуждены констатировать, что полного согласия между экспертами нет, а потому данные, приведенные в таблице, следует подвергнуть более тщательному математическому анализу.

