|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Алгоритмы обнаружения и коррекции ошибок
4.2. Введение в коды Рида-Соломона: принципы, архитектура и реализация
Коды Рида-Соломона были предложены в 1960 году Ирвином Ридом (Irving S. Reed) и Густавом Соломоном (Gustave Solomon), являвшимися сотрудниками Линкольнской лаборатории МТИ. Ключом к использованию этой технологии стало изобретение эффективного алгоритма декодирования Элвином Беликамфом (Elwyn Berlekamp; http://en.wikipedia.org/wiki/Berlekamp-Massey_algorithm), профессором Калифорнийского университета (Беркли). Коды Рида-Соломона (см. также http://www.4i2i.com/reed_solomon_codes.htm) базируются на блочном принципе коррекции ошибок и используются в огромном числе приложений в сфере цифровых телекоммуникаций и при построении запоминающих устройств. Коды Рида-Соломона применяются для исправления ошибок во многих системах:
- устройствах памяти (включая магнитные ленты, CD, DVD, штриховые коды, и т.д.);
- беспроводных или мобильных коммуникациях (включая сотовые телефоны, микроволновые каналы и т.д.);
- спутниковых коммуникациях;
- цифровом телевидении / DVB (digital video broadcast);
- скоростных модемах, таких как ADSL, xDSL и т.д.
На рис. 4.3 показаны практические приложения (дальние космические проекты) коррекции ошибок с использованием различных алгоритмов (Хэмминга, кодов свертки, Рида-Соломона и пр.). Данные и сам рисунок взяты из http://en.wikipedia.org/wiki/Reed-Solomon_error_correction.
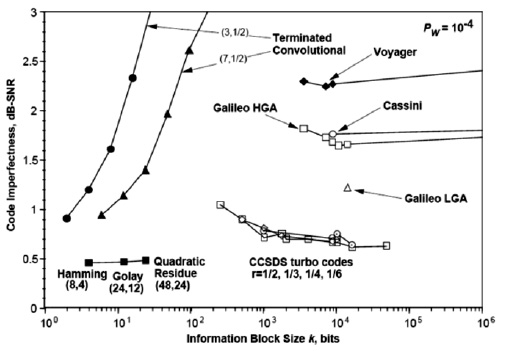
Рис. 4.3. Несовершенство кода, как функция размера информационного блока для разных задач и алгоритмов
Типовая система представлена ниже (см. http://www.4i2i.com/reed_solomon_codes.htm)
Кодировщик Рида-Соломона берет блок цифровых данных и добавляет дополнительные "избыточные" биты. Ошибки происходят при передаче по каналам связи или по разным причинам при запоминании (например, из-за шума или наводок, царапин на CD и т.д.). Декодер Рида-Соломона обрабатывает каждый блок, пытается исправить ошибки и восстановить исходные данные. Число и типы ошибок, которые могут быть исправлены, зависят от характеристик кода Рида-Соломона.
Свойства кодов Рида-Соломона
Коды Рида-Соломона являются субнабором кодов BCH и представляют собой линейные блочные коды. Код Рида-Соломона специфицируются как RS(n,k) s -битных символов.
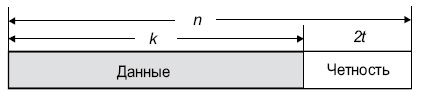
Это означает, что кодировщик воспринимает k информационных символов по s битов каждый и добавляет символы четности для формирования n символьного кодового слова. Имеется nk символов четности по s битов каждый. Декодер Рида-Соломона может корректировать до t символов, которые содержат ошибки в кодовом слове, где 2t = n–k.
Диаграмма, представленная ниже, показывает типовое кодовое слово Рида-Соломона:
Пример. Популярным кодом Рида-Соломона является RS(255, 223) с 8-битными символами. Каждое кодовое слово содержит 255 байт, из которых 223 являются информационными и 32 байтами четности. Для этого кода
n = 255, k = 223, s = 8
2t = 32, t = 16
Декодер может исправить любые 16 символов с ошибками в кодовом слове: то есть ошибки могут быть исправлены, если число искаженных байт не превышает 16.
При размере символа s, максимальная длина кодового слова ( n ) для кода Рида-Соломона равна n = 2s – 1.
Например, максимальная длина кода с 8-битными символами ( s = 8 ) равна 255 байтам.
Коды Рида-Соломона могут быть в принципе укорочены путем обнуления некоторого числа информационных символов на входе кодировщика (передавать их в этом случае не нужно). При передаче данных декодеру эти нули снова вводятся в массив.
Пример. Код (255, 223), описанный выше, может быть укорочен до (200, 168). Кодировщик будет работать с блоком данных 168 байт, добавит 55 нулевых байт, сформирует кодовое слово (255, 223) и передаст только 168 информационных байт и 32 байта четности.
Объем вычислительной мощности, необходимой для кодирования и декодирования кодов Рида-Соломона, зависит от числа символов четности. Большое значение t означает, что большее число ошибок может быть исправлено, но это потребует большей вычислительной мощности по сравнению с вариантом при меньшем t.
Ошибки в символах
Одна ошибка в символе происходит, когда 1 бит символа оказывается неверным или когда все биты неверны.
Пример. Код RS(255,223) может исправить до 16 ошибок в символах. В худшем случае, могут иметь место 16 битовых ошибок в разных символах (байтах). В лучшем случае, корректируются 16 полностью неверных байт, при этом исправляется 16 x 8 = 128 битовых ошибок.
Коды Рида-Соломона особенно хорошо подходят для корректировки кластеров ошибок (когда неверными оказываются большие группы бит кодового слова, следующие подряд).
Декодирование
Алгебраические процедуры декодирования Рида-Соломона могут исправлять ошибки и потери. Потерей считается случай, когда положение неверного символа известно. Декодер может исправить до t ошибок или до 2t потерь. Данные о потере (стирании) могут быть получены от демодулятора цифровой коммуникационной системы, т.е. демодулятор помечает полученные символы, которые вероятно содержат ошибки.
Когда кодовое слово декодируется, возможны три варианта.
- Если 2s + r < 2t ( s ошибок, r потерь), тогда исходное переданное кодовое слово всегда будет восстановлено. В противном случае
- Декодер детектирует ситуацию, когда он не может восстановить исходное кодовое слово. или
- Декодер некорректно декодирует и неверно восстановит кодовое слово без какого-либо указания на этот факт.
Вероятность каждого из этих вариантов зависит от типа используемого кода Рида-Соломона, а также от числа и распределения ошибок.