|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Алгоритмы обнаружения и коррекции ошибок
Преимущество кодирования
Преимущество использования кодов Рида-Соломона заключается в том, что вероятность сохранения ошибок в декодированных данных обычно много меньше, чем вероятность ошибок, если коды Рида-Соломона не используются. Это часто называется выигрышем кодирования.
Пример. Пусть имеется цифровая телекоммуникационная система, работающая с BER (Bit Error Ratio), равной 10-9, т.е. не более 1 из 109 бит передается с ошибкой. Такого результата можно достичь путем увеличения мощности передатчика или применением кодов Рида-Соломона (либо другого типа коррекции ошибок). Алгоритм Рида-Соломона позволяет системе достичь требуемого уровня BER с более низкой выходной мощностью передатчика.
Архитектура кодирования и декодирования кодов Рида-Соломона
Кодирование и декодирование Рида-Соломона может быть выполнено аппаратно или программно.
Арифметика конечного поля Галуа
Коды Рида-Соломона базируются на специальном разделе математики – полях Галуа (GF) или конечных полях. Арифметические действия (+,-, x, / и т.д.) над элементами конечного поля дают результат, который также является элементом этого поля. Кодировщик или декодер РидаСоломона должны уметь выполнять эти арифметические операции. Эти операции для своей реализации требуют специального оборудования или специализированного программного обеспечения.
Образующий полином
Кодовое слово Рида-Соломона формируется с привлечением специального полинома. Все корректные кодовые слова должны делиться без остатка на эти образующие полиномы. Общая форма образующего полинома имеет вид
g(x) = (x – ai)(x – ai+1)...(x – ai+2t)
а кодовое слово формируется с помощью операции
c(x) = g(x).i(x)
где g(x) является образующим полиномом, i(x) представляет собой информационный блок, c(x) – кодовое слово, называемое простым элементом поля.
Пример. Генератор для RS(255, 249)
g(x)= (x – a0)(x – a1)(x – a2)(x – a3)(x – a4)(x – a5) g(x)= x6 + g5x5 + g3x3 + g2x2 + g1x1 + g0
Архитектура кодировщика
2t символов четности в кодовом слове Рида-Соломона определяются из следующего соотношения:
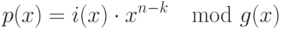
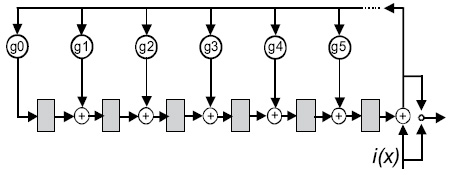
Ниже показана схема реализации кодировщика для версии RS(255,249):
Каждый из 6 регистров содержит в себе символ (8 бит). Арифметические операторы выполняют сложение или умножение на символ как на элемент конечного поля.
Архитектура декодера
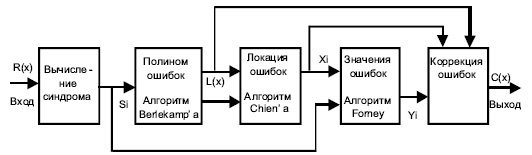
Общая схема декодирования кодов Рида-Соломона показана ниже на рис. 4.7.
Обозначения:
- r(x) – Полученное кодовое слово
- Si – Синдромы
- L(x) – Полином локации ошибок
- Xi – Положения ошибок
- Yi – Значения ошибок
- c(x) – Восстановленное кодовое слово
- v – Число ошибок
Полученное кодовое слово r(x) представляет собой исходное (переданное) кодовое слово c(x) плюс ошибки:
r(x) = c(x) + e(x)
Декодер Рида-Соломона пытается определить позицию и значение ошибки для t ошибок (или 2t потерь) и исправить ошибки и потери.
Вычисление синдрома
Вычисление синдрома похоже на вычисление четности. Кодовое слово Рида-Соломона имеет 2t синдромов, это зависит только от ошибок (а не передаваемых кодовых слов). Синдромы могут быть вычислены путем подстановки 2t корней образующего полинома g(x) в r(x).
Нахождение позиций символьных ошибок
Это делается путем решения системы уравнений с t неизвестными. Существует несколько быстрых алгоритмов для решения этой задачи. Эти алгоритмы используют особенности структуры матрицы кодов РидаСоломона и сильно сокращают необходимую вычислительную мощность. Делается это в два этапа.
1. Определение полинома локации ошибок.
Это может быть сделано с помощью алгоритма Berlekamp-Massey или алгоритма Эвклида. Алгоритм Эвклида используется чаще на практике, так как его легче реализовать, однако алгоритм Berlekamp-Massey позволяет получить более эффективную реализацию оборудования и программ.
2. Нахождение корней этого полинома. Это делается с привлечением алгоритма поиска Chien.
Нахождение значений символьных ошибок
Здесь также нужно решить систему уравнений с t неизвестными. Для решения используется быстрый алгоритм Forney.
Реализация кодировщика и декодера Рида-Соломона. Аппаратная реализация
Существует несколько коммерческих аппаратных реализаций. Имеется много разработанных интегральных схем, предназначенных для кодирования и декодирования кодов Рида-Соломона. Эти ИС допускают определенный уровень программирования (например RS(255, k), где t может принимать значения от 1 до 16).
Программная реализация
До недавнего времени программные реализации в "реальном времени" требовали слишком большой вычислительной мощности практически для всех кодов Рида-Соломона. Главной трудностью в программной реализации кодов Рида-Соломона являлось то, что процессоры общего назначения не поддерживают арифметические операции для поля Галуа. Однако оптимальное составление программ в сочетании с возросшей вычислительной мощностью позволяют получить вполне приемлемые результаты для относительно высоких скоростей передачи данных.