Операторы языка C#
Бесконечность и компьютеры. Вычисления с точностью varepsilon>
Бесконечность для математики естественна. Множество целых чисел бесконечно, множество рациональных чисел бесконечно, множество вещественных чисел бесконечно. Но если элементы первых двух множеств можно пронумеровать, то последнее множество несчетно. Сколь угодно малый промежуток вещественной оси мы бы ни взяли, там находится бесконечно много вещественных чисел. Число  и другие иррациональные числа задаются бесконечным числом цифр, не имеющим периода. Многие базисные определения в математике основаны на понятии предела и стремлении к бесконечности.
и другие иррациональные числа задаются бесконечным числом цифр, не имеющим периода. Многие базисные определения в математике основаны на понятии предела и стремлении к бесконечности.
Мир компьютеров - это конечный мир, хотя в нем и присутствует стремление к бесконечности. Множества, с которыми приходится оперировать в мире компьютера, всегда конечны. Тип целых чисел в языках программирования - int - всегда задает конечное множество целых из некоторого фиксированного диапазона. В библиотеке FCL это наглядно подтверждается самими именами целочисленных типов System.Int16, System.Int32, System.Int64. Типы вещественных чисел - double, float - задают конечные множества. Это достигается не только тем, что диапазон задания вещественных чисел ограничен, но и ограничением числа значащих цифр, задающих вещественное число. Поэтому для вещественных чисел компьютера всегда можно указать такие два числа, между которыми нет никаких других чисел. Иррациональности компьютер не знает - число  всегда задается конечным числом цифр.
всегда задается конечным числом цифр.
Там, где в математике идет речь о пределах, бесконечных суммах, сходимости к бесконечности, в компьютерных вычислениях аналогичные задачи сводятся к вычислениям с заданной точностью - с точностью  . Рассмотрим, например, задачу о вычислении предела числовой последовательности:
. Рассмотрим, например, задачу о вычислении предела числовой последовательности:
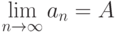
По определению число A является пределом числовой последовательности, если для любого сколь угодно малого числа  существует такой номер N, зависящий от
существует такой номер N, зависящий от  , что для всех n, больших N, числа
, что для всех n, больших N, числа 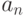 находятся в
находятся в  -окрестности числа A. Это определение дает основу для вычисления значения предела A. Понятно, что получить точное значение A во многих случаях принципиально невозможно, - его можно вычислить лишь с некоторой точностью и тоже не сколь угодно малой, поскольку, как уже говорилось, есть понятие "машинного нуля" - минимального числа, все значения меньше которого воспринимаются как нуль. В одной из задач требуется вычислить значение числа
-окрестности числа A. Это определение дает основу для вычисления значения предела A. Понятно, что получить точное значение A во многих случаях принципиально невозможно, - его можно вычислить лишь с некоторой точностью и тоже не сколь угодно малой, поскольку, как уже говорилось, есть понятие "машинного нуля" - минимального числа, все значения меньше которого воспринимаются как нуль. В одной из задач требуется вычислить значение числа  как предел числовой последовательности. Оставаясь в рамках стандартных множеств чисел (double, float), принципиально невозможно получить точное значение этого числа,
поскольку в этих множествах нет иррациональных чисел с бесконечным числом цифр. Но можно получить значение этого числа с некоторой точностью. Когда два соседних члена последовательности -
как предел числовой последовательности. Оставаясь в рамках стандартных множеств чисел (double, float), принципиально невозможно получить точное значение этого числа,
поскольку в этих множествах нет иррациональных чисел с бесконечным числом цифр. Но можно получить значение этого числа с некоторой точностью. Когда два соседних члена последовательности - 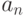 и
и 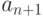 - начинают отличаться на величину, по модулю меньшую, чем
- начинают отличаться на величину, по модулю меньшую, чем  , то можно полагать, что оба члена последовательности попали в
, то можно полагать, что оба члена последовательности попали в  -окрестность числа A и
-окрестность числа A и 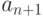 можно принять за приближенное значение числа A. Это рассуждение верно только при условии, что последовательность действительно имеет предел. В противном случае этот прием может привести к ошибочным выводам. Например, последовательность, элементы которой равны 1, если индекс элемента делится на 3, и равны 2, если индекс не делится на 3. Очевидно, что у этой последовательности предела нет, хотя существуют два полностью совпадающих соседних члена последовательности.
можно принять за приближенное значение числа A. Это рассуждение верно только при условии, что последовательность действительно имеет предел. В противном случае этот прием может привести к ошибочным выводам. Например, последовательность, элементы которой равны 1, если индекс элемента делится на 3, и равны 2, если индекс не делится на 3. Очевидно, что у этой последовательности предела нет, хотя существуют два полностью совпадающих соседних члена последовательности.
Большинство задач этого раздела посвящено вычислениям значения функций, заданных разложением в бесконечный сходящийся ряд. И здесь не ставится задача получения абсолютно точного результата. Достаточно вычислить значение функции с заданной точностью  . На практике вычисления останавливаются, когда текущий член суммы становится по модулю меньше заданного
. На практике вычисления останавливаются, когда текущий член суммы становится по модулю меньше заданного  . Опять-таки, чтобы этот прием корректно работал, необходима сходимость ряда. Контрпримером является задача, где вычисляется сумма гармонического ряда. Здесь для любого заданного
. Опять-таки, чтобы этот прием корректно работал, необходима сходимость ряда. Контрпримером является задача, где вычисляется сумма гармонического ряда. Здесь для любого заданного  текущий член суммы, начиная с некоторого номера, становится меньше
текущий член суммы, начиная с некоторого номера, становится меньше  , но ряд расходится, и последовательность конечных сумм ряда не имеет предела.
, но ряд расходится, и последовательность конечных сумм ряда не имеет предела.
Рассмотрим задачу вычисления функции с использованием ее разложения в бесконечный сходящийся ряд:
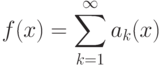
Вот возможный шаблон ее решения:
public double f(double x)
{
double S=0,ak=1, eps=1e-8;
while(Math.Abs(ak) >eps)
{
//Вычислить ak
S+=ak;
}
return(S);
}При применении этого шаблона следует:
- получить при возможности рекуррентную формулу, используя для вычисления нового значения ak ранее вычисленные значения;
- использовать по возможности свойства функции f(x) для ускорения сходимости ak к нулю, например, привести x к минимально возможному диапазону для периодических функций;
- помнить, что данный шаблон применим только тогда, когда ряд является сходящимся;
- понимать, что выполнение условия (|ak| < eps ) еще не означает, что значение функции вычислено с точностью eps. Строго говоря, необходимо иметь оценку остаточного члена ряда. На практике этим обстоятельством зачастую можно пренебрегать, уменьшая при необходимости eps и достигая тем самым нужной точности вычисления f(x).
Во всех задачах этого раздела задается точность вычислений  - малое вещественное число. Обычно, если требуется получить результат с точностью до 5-6 значащих цифр, то
- малое вещественное число. Обычно, если требуется получить результат с точностью до 5-6 значащих цифр, то  задается константой
задается константой  (1e-8 - 1e-9).
(1e-8 - 1e-9).
- 57. Вычислить с заданной точностью значение числа
 , используя следующее разложение в ряд:Минимизируйте время его вычисления в условных единицах. Сравните вычисленное значение
, используя следующее разложение в ряд:Минимизируйте время его вычисления в условных единицах. Сравните вычисленное значение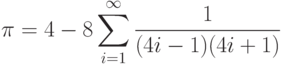
 со стандартным значением PI, возвращаемым классом Math. Для разных значений
со стандартным значением PI, возвращаемым классом Math. Для разных значений  вычислите n - число членов суммы, требуемых для достижения заданной точности.
вычислите n - число членов суммы, требуемых для достижения заданной точности. - 58. Вычислить с заданной точностью значение числа
 , используя следующее разложение в ряд:Минимизируйте время его вычисления в условных единицах. Сравните вычисленное значение
, используя следующее разложение в ряд:Минимизируйте время его вычисления в условных единицах. Сравните вычисленное значение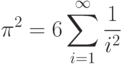
 со стандартным значением PI, возвращаемым классом Math. Для разных значений
со стандартным значением PI, возвращаемым классом Math. Для разных значений  вычислите n - число членов суммы, требуемых для достижения заданной точности.
вычислите n - число членов суммы, требуемых для достижения заданной точности. - 59. Вычислить с заданной точностью значение числа
 , используя следующее разложение в ряд:Предварительно следует записать рекуррентное соотношение для текущего члена суммы. Минимизируйте время его вычисления в условных единицах. Сравните вычисленное значение
, используя следующее разложение в ряд:Предварительно следует записать рекуррентное соотношение для текущего члена суммы. Минимизируйте время его вычисления в условных единицах. Сравните вычисленное значение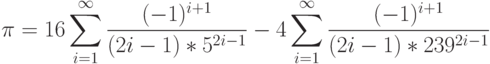
 со стандартным значением PI, возвращаемым классом Math. Для разных значений
со стандартным значением PI, возвращаемым классом Math. Для разных значений  вычислите n - число членов суммы, требуемых для достижения заданной точности.
вычислите n - число членов суммы, требуемых для достижения заданной точности. - 60. Вычислить с заданной точностью значение числа e, используя следующее разложение в ряд:Предварительно следует записать рекуррентное соотношение для текущего члена суммы. Минимизируйте время его вычисления в условных единицах. Сравните вычисленное значение e со стандартным значением E, возвращаемым классом Math. Для разных значений
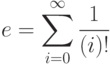
 вычислите n - число членов суммы, требуемых для достижения заданной точности.
вычислите n - число членов суммы, требуемых для достижения заданной точности. - 61. Пусть
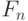 и
и 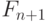 - два соседних числа Фибоначчи. Найти с заданной точностью предел отношения
- два соседних числа Фибоначчи. Найти с заданной точностью предел отношения 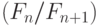 при
при 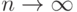 . Сравнить этот предел с "золотым сечением" - числом x. Напомню, золотое сечение строится следующим образом. Возьмем отрезок единичной длины и разделим его на две неравные части - большую x и меньшую y=1-x. Сечение называется "золотым", если отношение целого к большей части равно отношению большей части к меньшей: x/(1-x) = 1/x.
. Сравнить этот предел с "золотым сечением" - числом x. Напомню, золотое сечение строится следующим образом. Возьмем отрезок единичной длины и разделим его на две неравные части - большую x и меньшую y=1-x. Сечение называется "золотым", если отношение целого к большей части равно отношению большей части к меньшей: x/(1-x) = 1/x. - 62. Даны два положительных числа b и d. Пусть:Вычислить с заданной точностью пределы

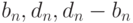 .
. - 63. Пусть x и y=1-x задают золотое сечение отрезка единичной длины (см. задачу 1.104). Пусть задано число
 , такое, что
, такое, что 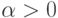 и
и  . Вычислить с заданной точностью предел последовательности
. Вычислить с заданной точностью предел последовательности 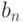 , где
, где 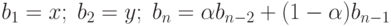
- 64. Дано вещественное число x. Вычислить с заданной точностью
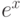 :Указание: для ускорения вычислений используйте разложение в ряд только для дробной части числа x. Используйте умножение и константу e для вычисления
:Указание: для ускорения вычислений используйте разложение в ряд только для дробной части числа x. Используйте умножение и константу e для вычисления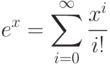
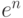 , где n - это целая часть числа x.
, где n - это целая часть числа x. - 65. Дано вещественное число x. Вычислить с заданной точностью sin(x):Указание: для ускорения вычислений используйте разложение в ряд только для приведенного значения числа x. Помните, что sin(x) - это периодическая функция, так что всегда можно привести x к интервалу
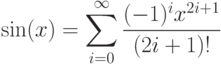
![[-\pi, \pi]](/sites/default/files/tex_cache/86f9a3a2cc344b78b146c202b2226bae.png) .
. - 66. Дано вещественное число x, такое, что |x| <1. Вычислить с заданной точностью arcsin(x):
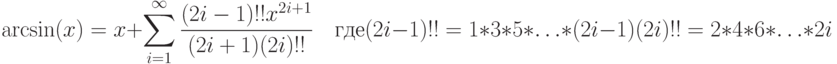
- 67. Дано вещественное число x. Вычислить с заданной точностью cos(x):Указание: для ускорения вычислений используйте разложение в ряд только для приведенного значения числа x. Помните, что cos(x) - это периодическая функция, так что всегда можно привести x к интервалу
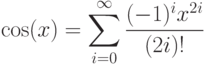
![[-\pi, \pi]](/sites/default/files/tex_cache/86f9a3a2cc344b78b146c202b2226bae.png) .
. - 68. Дано вещественное число x, такое, что |x| <1. Вычислить с заданной точностью arccos(x):
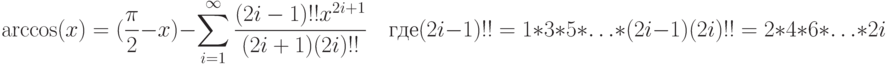
- 69. Дано вещественное число x >0. Вычислить с заданной точностью ln(x):
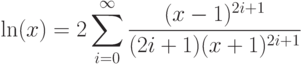
- 70. Дано вещественное число 0 < x < 2. Вычислить с заданной точностью ln(x):
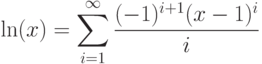
- 71. Дано вещественное число x. Вычислить с заданной точностью tg(x):где
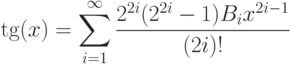
 определяются следующим соотношением:Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что tg(x) - это периодическая функция, так что всегда можно привести x к интервалу
определяются следующим соотношением:Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что tg(x) - это периодическая функция, так что всегда можно привести x к интервалу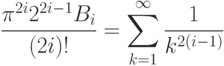
![[-\pi/2, \pi/2]](/sites/default/files/tex_cache/16174be2a587fdc8055e3d1699c5ff81.png) .
. - 72. Дано вещественное число x . Вычислить с заданной точностью arctg(x):
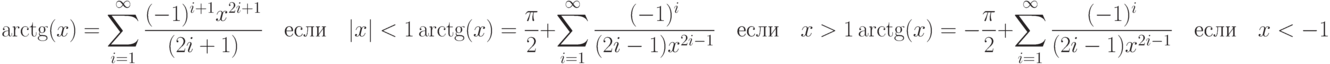
- 73. (**) Дано вещественное число x. Вычислить с заданной точностью ctg(x):где
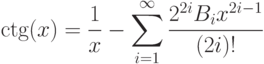
 определяются следующим соотношением:Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что сtg(x) - это периодическая функция, так что всегда можно привести x к интервалу
определяются следующим соотношением:Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что сtg(x) - это периодическая функция, так что всегда можно привести x к интервалу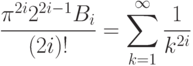
![[-\pi/2, \pi/2]](/sites/default/files/tex_cache/16174be2a587fdc8055e3d1699c5ff81.png) .
. - 74. Дано вещественное число x . Вычислить с заданной точностью arcсtg(x):
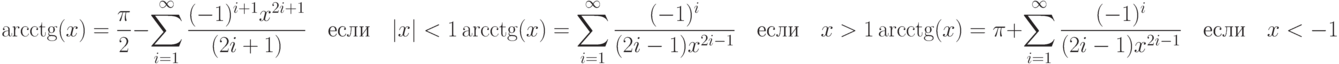
- 75. (**) Дано вещественное число x. Вычислить с заданной точностью sc(x):где
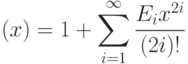
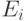 определяются следующим соотношением:Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что sc(x) - это периодическая функция, так что всегда можно привести x к интервалу
определяются следующим соотношением:Указание: используйте разложение в ряд только для приведенного значения числа x. Помните, что sc(x) - это периодическая функция, так что всегда можно привести x к интервалу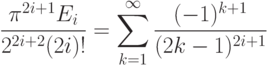
![[-\pi, \pi]](/sites/default/files/tex_cache/86f9a3a2cc344b78b146c202b2226bae.png) .
. - 76. Дано вещественное число x. Вычислить с заданной точностью sh(x):Указание: гиперболический синус sh(x) не является периодической функцией, поэтому никакого приведения x выполнять не следует.
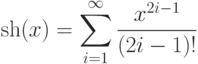
- 77. Дано вещественное число x. Вычислить с заданной точностью ch(x):Указание: гиперболический косинус ch(x) не является периодической функцией, поэтому никакого приведения x выполнять не следует.
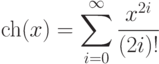
- 78. Дано вещественное число x. Вычислить с заданной точностью Arcsh(x):
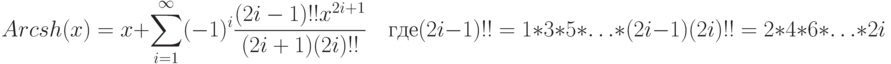
Проекты
- (*) Постройте класс MyMath, имеющий те же методы, что и класс Math библиотеки FCL.
- (**) Постройте Калькулятор, позволяющий использовать для вычислений как методы класса Math, так и MyMath, и сравнивать результаты по точности и времени вычислений.

