Опубликован: 02.12.2009 | Уровень: для всех | Доступ: платный | ВУЗ: Тверской государственный университет
Лекция 4:
Операторы языка C#
Рекуррентные вычисления
- 36. Вычислить
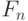 - число Фибоначчи с номером n, где
- число Фибоначчи с номером n, где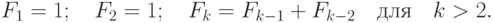
- 37. Дано натуральное число n и вещественные числа b и d. Вычислить сумму членов арифметической прогрессии:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, чтобы его вычисление требовало ровно одного сложения.
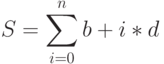
- 38. Дано натуральное число n и вещественные числа b и d. Вычислить сумму членов геометрической прогрессии:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, чтобы его вычисление требовало ровно одного умножения.
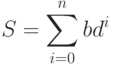
- 39. Дано натуральное число n. Вычислить:где
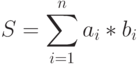
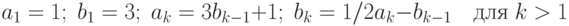
- 40. Даны натуральные числа n и m (50<m<n). Вычислить:где
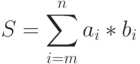
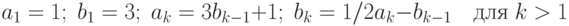
- 41. Даны натуральные числа n и m (50<m<n). Вычислить:где
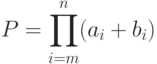
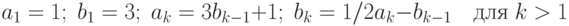
- 42. Дано натуральное число n и вещественное число x. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, чтобы его вычисление выполнялось за время, равное 12 уе. (см. задачи предыдущей главы). Сравните вычисленное значение S со значением
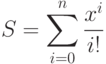
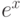 . Вычислите разность
. Вычислите разность  при различных значениях n и x.
при различных значениях n и x. - 43. Дано натуральное число n и вещественное число x. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, чтобы его вычисление выполнялось за время, равное 27 уе. (см. задачи предыдущей главы). Сравните вычисленное значение S со значением sin(x). Вычислите разность | S - sin(x)| при различных значениях n и x.
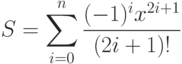
- 44. Дано натуральное число n и вещественное число x, такое, что |x| <1. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, минимизируя время его вычисления. Сравните вычисленное значение S со значением arcsin(x). Вычислите разность | S - arcsin(x)| при различных значениях n и x.

- 45. Дано натуральное число n и вещественное число x. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, чтобы его вычисление выполнялось за время, равное 27 уе. (см. задачу 1.30). Сравните вычисленное значение S со значением cos(x). Вычислите разность | S - cos(x)| при различных значениях n и x.
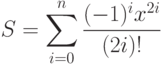
- 46. Дано натуральное число n и вещественное число x, такое, что |x| <1. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, минимизируя время его вычисления. Сравните вычисленное значение S со значением arccos(x). Вычислите разность | S - arccos(x)| при различных значениях n и x.
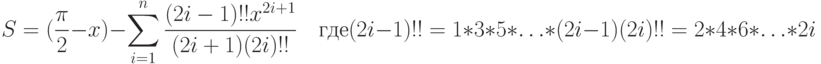
- 47. Дано натуральное число n и вещественное число x >0. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы. Минимизируйте время его вычисления в условных единицах. Сравните вычисленное значение S со значением ln(x). Вычислите разность | S - ln(x)| при различных значениях n и x.
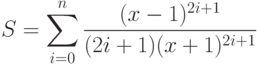
- 48. (**) Даны натуральные числа n и m и вещественное число x, такое, что
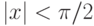 . Вычислить:где
. Вычислить:где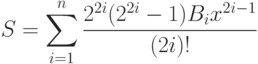
 определяются следующим соотношением:Предварительно следует записать рекуррентные соотношения, как для получения чисел
определяются следующим соотношением:Предварительно следует записать рекуррентные соотношения, как для получения чисел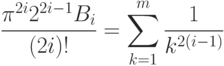
 , так и для вычисления S. Сравните вычисленное значение S со значением tg(x). Вычислите разность | S - tg(x)| при различных значениях n и x.
, так и для вычисления S. Сравните вычисленное значение S со значением tg(x). Вычислите разность | S - tg(x)| при различных значениях n и x. - 49. (*) Даны натуральные числа n и m и вещественное число x, такое, что
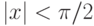 . Вычислить:Сравните вычисленное значение S со значением tg(x). Вычислите разность | S - tg(x)| при различных значениях n и x.
. Вычислить:Сравните вычисленное значение S со значением tg(x). Вычислите разность | S - tg(x)| при различных значениях n и x.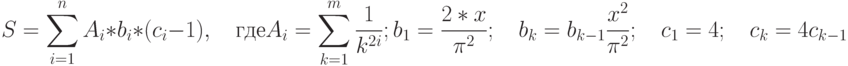
- 50. Дано натуральное число n и вещественное число x . Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, минимизируя время его вычисления. Сравните вычисленное значение S со значением arctg(x). Вычислите разность | S - arctg(x)| при различных значениях n и x.
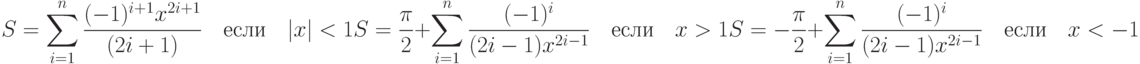
- 51. (**) Даны натуральные числа n и m и вещественное число x, такое, что
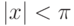 . Вычислить:где
. Вычислить:где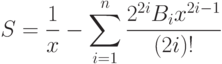
 определяются следующим соотношением:Предварительно следует записать рекуррентные соотношения как для получения чисел
определяются следующим соотношением:Предварительно следует записать рекуррентные соотношения как для получения чисел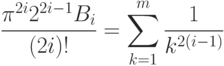
 , так и для вычисления S. Сравните вычисленное значение S со значением ctg(x). Вычислите разность | S - ctg(x)| при различных значениях n и x.
, так и для вычисления S. Сравните вычисленное значение S со значением ctg(x). Вычислите разность | S - ctg(x)| при различных значениях n и x. - 52. Дано натуральное число n и вещественное число x . Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, минимизируя время его вычисления. Сравните вычисленное значение S со значением arcctg(x). Вычислите разность | S - arcctg(x)| при различных значениях n и x.
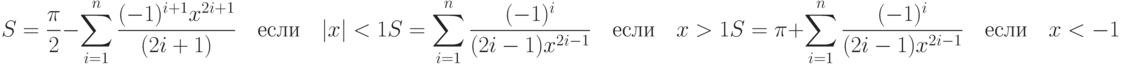
- 53. (**) Даны натуральные числа n и m и вещественное число x, такое, что
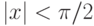 . Вычислить:где
. Вычислить:где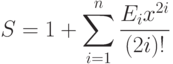
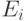 определяются следующим соотношением:Предварительно следует записать рекуррентные соотношения как для получения чисел
определяются следующим соотношением:Предварительно следует записать рекуррентные соотношения как для получения чисел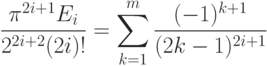
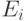 , так и для вычисления S. Сравните вычисленное значение S со значением sc(x). Вычислите разность | S - sc(x)| при различных значениях n и x.
, так и для вычисления S. Сравните вычисленное значение S со значением sc(x). Вычислите разность | S - sc(x)| при различных значениях n и x. - 54. Дано натуральное число n и вещественное число x. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, минимизируя время его вычисления. Сравните вычисленное значение S со значением sh(x). Вычислите разность | S - sh(x)| при различных значениях n и x.
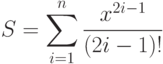
- 55. Дано натуральное число n и вещественное число x. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, минимизируя время его вычисления. Сравните вычисленное значение S со значением ch(x). Вычислите разность | S - ch(x)| при различных значениях n и x.

- 56. Дано натуральное число n и вещественное число x, такое, что |x| <1. Вычислить:Предварительно следует записать рекуррентное соотношение для текущего члена суммы, минимизируя время его вычисления. Сравните вычисленное значение S со значением Arcsh(x). Вычислите разность | S - Arcsh(x)| при различных значениях n и x.