Операторы языка C#
Вычисление сумм, произведений и рекуррентные соотношения
Повторю то, что уже говорилось при рассмотрении примера в первой лекции. Вычисление конечных сумм и произведений - это наиболее часто встречающийся тип элементарных задач, шаблон решения которых должен быть заучен как 2*2. Для вычисления суммы:
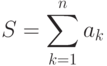
можно применить следующий шаблон:
S=0;
for(int k=1; k<=n; k++)
{
//Вычислить текущий член суммы ak
…
S+=ak;
}Часто приходится пользоваться слегка расширенным шаблоном:
Init;
for(int k=1; k<=n; k++)
{
//Вычислить текущий член суммы ak
…
S+=ak;
}В этом шаблоне Init представляет группу операторов, которые инициализируют значения переменных, используемых в цикле, значениями, обеспечивающими корректность применения цикла. В частном случае, рассмотренном выше, инициализация сводится к заданию значения переменной S. Заметьте, если перед началом цикла не позаботиться о том, чтобы эта переменная была равна нулю, то после завершения цикла результат не будет верным.
В этой схеме основные проблемы могут быть связаны с вычислением текущего члена суммы ak. Нужно понимать, что ak - это простая переменная, а не массив. Значения этой переменной вычисляются заново на каждом шаге цикла, задавая очередной член суммирования. Кроме того, следует заботиться об эффективности вычислений, применяя два основных правила, позволяющие уменьшить время вычислений.
Чистка цикла. Все вычисления, не зависящие от k, должны быть вынесены из цикла (в раздел Init).
Рекуррентная формула. Часто можно уменьшить время вычислений ak, используя предыдущее значение ak. Иногда приходится вводить дополнительные переменные, хранящие уже вычисленные значения нескольких членов суммы. Рекуррентная формула выражает новое значение ak через предыдущее значение и дополнительные переменные, если они требуются. Начальные значения ak и дополнительных переменных должны быть корректно установлены перед выполнением цикла в разделе Init. Заметьте, что если начальное значение ak вычисляется в разделе Init до цикла, то схема слегка модифицируется - вначале выполняется прибавление ak к S, а затем новое значение ak вычисляется по рекуррентной формуле.
Рассмотрим пример. Пусть необходимо вычислить сумму:
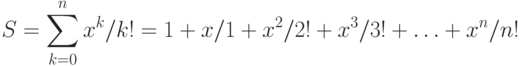
Тогда в соответствии с шаблоном
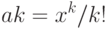
Можно построить рекуррентную формулу для ak, поскольку каждое следующее значение равно предыдущему значению, умноженному на x и деленному на k. Вычисление суммы задает следующий фрагмент программы:
int S =0;
int ak=1;
for(int k=0; k<=n; k++)
{
S+=ak;
//Вычислить текущий член суммы ak
ak *=x/k;
}Большинство задач этого раздела соответствуют этому шаблону. Рекуррентную формулу чаще всего можно получить, записав выражение для 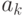 и
и 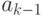 и вычислив затем их отношение. В некоторых задачах (они отмечены звездочкой) получение рекуррентной формулы может требовать больших усилий.
и вычислив затем их отношение. В некоторых задачах (они отмечены звездочкой) получение рекуррентной формулы может требовать больших усилий.
Начиная с этой задачи, мы будем в большинстве случаев опускать слова "Постройте консольное и Windows-приложение", полагая их подразумевающимися по умолчанию. Предполагается также, что консольное приложение позволяет проводить многократные эксперименты. При необходимости в консольном приложения предполагается построение меню.
- 24. Дано натуральное число n. Вычислить сумму первых n членов расходящегося гармонического ряда:
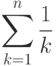
- 25. Дано натуральное число nmax и вещественное число b. Найти, если оно существует, такое наименьшее n, меньшее nmax, что:Если сумма nmax членов гармонического ряда меньше b, то необходимо выдать соответствующее сообщение.
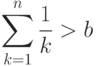
- 26. Дано натуральное число n. Вычислить сумму первых n членов ряда:При суммировании исключается каждый третий член.
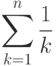
- 27. Дано натуральное число n. Вычислить сумму первых 2n членов ряда:Вычислить эту сумму четырьмя разными способами: последовательно слева направо, последовательно справа налево, слева направо, вычисляя вначале положительные члены ряда, затем отрицательные, справа налево, вычисляя вначале положительные члены ряда, затем отрицательные. Сравните результаты вычислений. Чем объясняется различие в последних цифрах при больших n? Как влияет на результат использование типов float или double для переменных, задающих суммы и текущий член при суммировании?
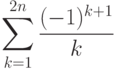
- 28. Дано натуральное число n. Вычислить сумму первых 2n членов ряда:
![\sum\limits_{k=1}^{2n} \frac{(-1)^{k+1}}{k\sqrt[k]{(k+1)}}](/sites/default/files/tex_cache/0f83246bc24b6c60f6dc138f23e23f45.png)
- 29. Дано натуральное число n. Вычислить произведение первых n членов ряда:
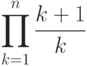
- 30. Даны натуральные числа n и k (n>=k). Вычислить биномиальный коэффициент
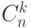 :
: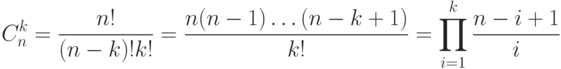
- 31. Даны натуральные числа n и m (n>=m). Вычислить сумму биномиальных коэффициентов:Следует напомнить, что определения функций суммы и произведения предполагают:
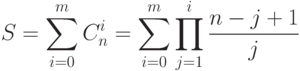
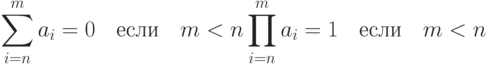
- 32. Дан массив B размерности n*m и массив C размерности m*n. Вычислить сумму диагональных элементов матрицы A = B*C:
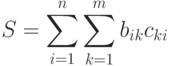
- 33. Дан массив B размерности n*m и массив C размерности m*n. Вычислить произведение диагональных элементов матрицы A = B*C:
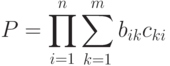
- 34. Даны натуральные числа n и m, вещественное x. Вычислить:
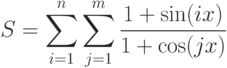
- 35. Даны натуральные числа n и m, вещественное x. Вычислить: