Простые числа

12.2. Испытание простоты чисел

Если формулы получения простых чисел, подобно формулам Ферма или Мерсенна, не гарантируют, что полученные числа — простые, то как мы можем генерировать большие простые числа для криптографии? Мы можем только выбрать случайно большое число и провести испытание, чтобы убедиться, что оно — простое.

Нахождение алгоритма, который правильно и эффективно проверяет очень большое целое число и устанавливает: данное число – простое это число или же составной объект, — всегда было проблемой в теории чисел и, следовательно, в криптографии. Однако, недавние исследования (одно из которых мы обсуждаем в этом разделе) выглядят очень перспективными.

Алгоритмы, которые решают эту проблему, могут быть разделены на две обширные категории — детерминированные алгоритмы и вероятностные алгоритмы. Ниже рассматриваются некоторые представители обеих категорий. Детерминированный алгоритм всегда дает правильный ответ. Вероятностный алгоритм дает правильный ответ в большинстве, но не во всех случаях. Хотя детерминированный алгоритм идеален, он обычно менее эффективен, чем соответствующий вероятностный.

Детерминированные алгоритмы

Детерминированный алгоритм, проверяющий простоту чисел, принимает целое число и выдает на выходе признак: это число — простое число или составной объект. До недавнего времени все детерминированные алгоритмы были неэффективны для нахождения больших простых чисел. Как мы коротко покажем, новые взгляды делают эти алгоритмы более перспективными.

Алгоритм теории делимости

Самое элементарное детерминированное испытание на простоту чисел — испытание на делимость. Мы используем в качестве делителей все числа, меньшие, чем 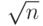. Если любое из этих чисел делит n, тогда n — составное. Алгоритм 12.1 показывает проверку на делимость в ее примитивной и очень неэффективной форме.

Алгоритм может быть улучшен, если проверять только нечетные номера. Он может быть улучшен далее, если использовать таблицу простых чисел между 2 и 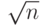. Число арифметических операций в алгоритме 12.1 — 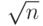. Если мы принимаем, что каждая арифметическая операция использует только операцию на один бит (чисто условное соглашение), тогда сложность разрядной операции алгоритма 12.1 — , где n_b – число битов в n. В больших системах, обозначаемых О, сложность может быть оценена O(2ⁿ): экспоненциально (см. приложение L). Другими словами, алгоритм делимости неэффективен, если n_b большое.

Пример 12.18

Предположим, что n имеет 200 битов. Какое число разрядных операций должен был выполнить алгоритм делимости?

Решение

Сложность побитовых операций этого алгоритма — . Это означает, что алгоритму необходимо провести 2¹⁰⁰ битовых операций. Если алгоритм имеет скорость 2³⁰ операций в секунду, то необходимо 2⁷⁰ секунд для проведения испытаний.

AKS-алгоритм

В 2002 г. индийские ученые Агравал, Каял и Сахсена (Agrawal, Kayal и Saxena) объявили, что они нашли алгоритм для испытания простоты чисел с полиномиальной сложностью времени разрядных операций 0 ((log₂n_b)). Алгоритм использует тот факт, что 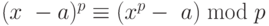. Интересно наблюдать, что некоторые будущие разработки делают этот алгоритм стандартным тестом для определения простоты чисел в математике и информатике.

Пример 12.19

Предположим, что n имеет 200 битов. Какое число разрядных операций должен был выполнить алгоритм AKS?

Решение

Сложность разрядной операции этого алгоритма — O((log ₂ n _b) ¹²). Это означает, что алгоритму надо только (log₂ 200) ¹² = 39 547 615 483 битовых операций. На компьютере, способном выполнить 1 миллиард битов в секунду, алгоритму требуется только 40 секунд.

Вероятностные алгоритмы

До AKS-алгоритма все эффективные методы для испытания простоты чисел были вероятностные. Эти методы могут использоваться еще некоторое время, пока AKS формально не принят как стандарт.

Вероятностный алгоритм не гарантирует правильность результата. Однако мы можем получить вероятность ошибки настолько маленькую, что это почти гарантирует, что алгоритм вырабатывает правильный ответ. Сложность разрядной операции алгоритма может стать полиномиальной, при этом мы допускаем небольшой шанс для ошибок. Вероятностный алгоритм в этой категории возвращает результат либо простое число, либо составной объект, основываясь на следующих правилах:

a. Если целое число, которое будет проверено, — фактически простое число, алгоритм явно возвратит простое число.

b. Если целое число, которое будет проверено, — фактически составной объект, алгоритм возвращает составной объект с вероятностью , но может возвратить простое число с 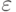вероятности. Вероятность ошибки может быть улучшена, если мы выполняем алгоритм несколько раз с различными параметрами или с использованием различных методов. Если мы выполняем алгоритм m раз, вероятность ошибки может уменьшиться до _m.

Тест Ферма

Первый вероятностный метод, который мы обсуждаем, — испытание простоты чисел тестом Ферма.

Если n — простое число, то .

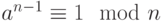Обратите внимание, что если n — простое число, то сравнение справедливо. Это не означает, что если сравнение справедливо, то n — простое число. Целое число может быть простым числом или составным объектом. Мы можем определить следующие положения как тест Ферма:

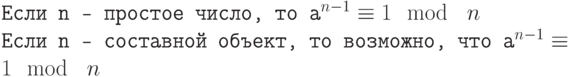
Простое число удовлетворяет тесту Ферма. Составной объект может пройти тест Ферма с вероятностью 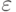. Сложность разрядной операции испытания Ферма равна сложности алгоритма, который вычисляет возведение в степень. Позже в этой лекции мы приводим алгоритм для быстрого возведения в степень со сложностью разрядной операции O(n_b ), где О — номер битов в n. Вероятность может быть улучшена, если проверка делается с несколькими числами (a₁, a₂ и так далее). Каждое испытание увеличивает вероятность, что испытуемое число – это простое число.

Пример 12.20

Проведите испытание Ферма для числа 561.

Решение

Используем в качестве основания число 2.

2^561-1 = 1 mod 561

Число прошло тест Ферма, но это — не простое число, потому что

.

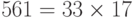Испытание квадратным корнем

В модульной арифметике, если n — простое число, то квадратный корень равен только 1 (либо +1, либо –1). Если n — составной объект, то квадратный корень — +1 или (-1), но могут быть и другие корни. Это называют испытанием простоты чисел квадратным корнем. Обратите внимание, что в модульной арифметике –1 означает n–1.

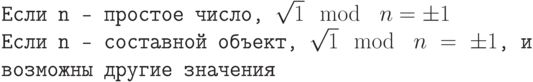
Пример 12.21

Каковы квадратные корни 1 mod n, если n равно 7 (простое число)?

Решение

Единственные квадратные корни 1 mod n – это числа 1 и –1. Мы можем видеть, что

12 = 1 mod 7	  (–1)2 = 1 mod 7
22 = 4 mod 7	  (–2)2 = 4 mod 7
32 = 2 mod 7	  (–3)2 = 2 mod 7

Заметим, что тест не дает результатов для 4, 5 и 6, потому что 4 = –3 mod 7, 5 = –2 mod 7 и 6 = –1 mod 7.

Пример 12.22

Каков квадратный корень из 1 mod n, если n равно 8 (составное)?

Решение

Имеется три решения: 1, 3, 5 и 7 (которые дают –1). Мы можем также видеть, что

12 = 1 mod 8	  (–1)2 = 1 mod 8
32 = 1 mod 8	  (–5)2 = 1 mod 8

Пример 12.23

Каков квадратный корень из 1 mod n, если n равно 17 (простое)?

Решение

Имеются только два решения, соответствующие поставленной задаче: это 1 и (–1).

12 = 1 mod 17	  (-1)2 = 1 mod 17
22 = 4 mod 17	  (-2)2 = 4 mod 17
32 = 9 mod 17	  (-3)2 = 9 mod 17
42 = 16 mod 17	  (-4)2 = 16 mod 17
52 = 8 mod 17	  (-5)2 = 8 mod 17
62 = 2 mod 17	  (-6)2 = 2 mod 17
72 = 15 mod 17	  (-7)2 = 15 mod 17
82 = 13 mod 17	  (-8)2 = 13 mod 17

Заметим, что не надо проверять целые числа, большие 8, потому что 9 = –8 mod 17

Пример 12.24

Каков квадратный корень из 1 mod n, если n равно 22 (составное)?

Решение

Сюрприз в том, что имеется только два решения: +1 и –1, хотя 22 — составное число.

12    = 1 mod 22
(-1)2 = 1 mod 22

Хотя во многих случаях имеется испытание, которое показывает нам однозначно, что число составное, но это испытание провести трудно. Когда дано число n, то все числа, меньшие, чем n (кроме чисел 1 и n–1), должны быть возведены в квадрат, чтобы гарантировать, что ни одно из них не равно 1. Это испытание может использоваться для чисел (не +1 или –1), которые в квадрате по модулю n дают значение 1. Этот факт помогает в испытании Миллера–Рабина, которое рассматривается в следующем разделе.