| Видео курс есть это программы, спасибо |
Использование функций. Часть 1
Возведение в степень
Для возведения в степень используют функцию СТЕПЕНЬ.
Синтаксис функции
СТЕПЕНЬ(А;В),
где A – число, возводимое в степень;
В – показатель степени, в которую возводится число.
Отрицательные числа можно возводить только в степень, значение которой является целым числом. В остальном ограничений на возведение в степень нет.
Для извлечения квадратного корня можно использовать функцию КОРЕНЬ.
Синтаксис функции
КОРЕНЬ(А),
где A – число, из которого извлекают квадратный корень.
Нельзя извлекать корень из отрицательных чисел.
Тригонометрические вычисления
В Microsoft Excel можно выполнять как прямые, так и обратные тригонометрические вычисления, то есть, зная значение угла, находить значения тригонометрических функций или, зная значение функции, находить значение угла.
Синтаксис всех прямых тригонометрических функций одинаков. Например, синтаксис функции SIN.
SIN(А),
где A – угол в радианах, для которого определяется синус.
Точно так же одинаков и синтаксис всех обратных тригонометрических функций. Например, синтаксис функции АSIN
АSIN(А),
где A – число, равное синусу определяемого угла.
Следует обратить внимание, что все тригонометрические вычисления производятся для углов, измеряемых в радианах. Для перевода в более привычные градусы следует использовать функции преобразования ( ГРАДУСЫ, РАДИАНЫ ) или самостоятельно переводить значения используя функцию ПИ ().
Функция ПИ () вставляет значение числа  (пи). Аргументов функция не имеет, но скобки после названия удалять нельзя.
(пи). Аргументов функция не имеет, но скобки после названия удалять нельзя.
Например, при необходимости рассчитать значение синуса угла, указанного в градусах, необходимо его умножить на ПИ()/180.
увеличить изображение
Рис. 7.7. Вычисление тригонометрических функций для углов, указанных в градусах
Преобразование чисел
Преобразование чисел может потребоваться при переводе углов из градусов в радианы и обратно, при определении абсолютной величины числа, при преобразовании арабских цифр в римские.
Для перевода значения угла, указанного в радианах, в градусы используют функцию ГРАДУСЫ.
Синтаксис функции
ГРАДУСЫ(А),
где А – угол в радианах, преобразуемый в градусы.
Для перевода значения угла, указанного в градусах, в радианы используют функцию РАДИАНЫ.
Синтаксис функции
РАДИАНЫ(А),
где А – угол в градусах, преобразуемый в радианы.
Функции ГРАДУСЫ и РАДИАНЫ удобно использовать с тригонометрическими функциями. Например, при необходимости рассчитать значение синуса угла, указанного в градусах (рис. 7.8), или рассчитать в градусах значение арксинуса (рис. 7.9).
увеличить изображение
Рис. 7.8. Вычисление тригонометрических функций для углов, указанных в градусах
увеличить изображение
Рис. 7.9. Вычисление углов в градусах при использовании тригонометрических функций
Для определения абсолютной величины числа используют функцию ABS. Абсолютная величина числа – это число без знака.
Синтаксис функции
ABS(А),
где А – число, для которого определяется абсолютное значение.
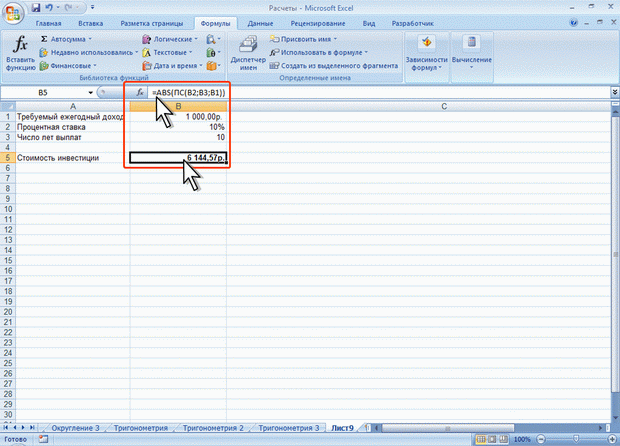
Функция ABS часто применяется для преобразования результатов вычислений с использованием финансовых функций, которые в силу своих особенностей дают отрицательный результат вычислений. Например, при расчете стоимости инвестиции с использованием функции ПС результат получается отрицательным, поскольку эту сумму необходимо заплатить. Для преобразования результата в положительное число можно использовать функцию ABS (рис. 7.10).
Для преобразования числа, записанного арабскими цифрами в число, записанное римскими цифрами, используют функцию РИМСКОЕ.
Синтаксис функции
РИМСКОЕ(А; В),
где А – число, записанное арабскими цифрами;
В – форма записи числа.
Если значение аргумента В не указано или указано число 0, то используется классическая форма записи римского числа. При значениях аргумента В от 1 до 4 используются различные формы упрощенной записи римских чисел.
Функцию РИМСКОЕ нельзя использовать для отрицательных чисел, а также для чисел больше 3999.