| ВКР |
Управление организационно-экономической устойчивостью промышленных корпоративных систем на основе динамического анализа состояния в условиях неопределенности
8.2. Метод динамического анализа состояния многопараметрического объекта
Способ динамического анализа состояния многопараметрического объекта или системы. Для решения задачи оперативного анализа воспользуемся методом динамического анализа состояния многопараметрического объекта, где в качестве такого объекта рассматриваем предприятие в целом, а диагностику и анализ его состояния осуществляем на основе классификации показателей, характеризующих организационно-экономическую устойчивость предприятия, разработанной в "Управление организационно-экономической устойчивостью промышленных корпоративных систем на основе динамического анализа состояния в условиях неопределенности" .
В решении данной задачи предлагается основываться на способе оперативного динамического анализа нечеткого состояния многопараметрического объекта (МПО), позволяющего реализовывать принцип предыстории функционирования МПО на основе проведения целевой декомпозиции исходного множества многопараметрического пространства состояний на классы четких и нечетких состояний разнородных динамических параметров.
Этот метод позволяет обеспечить визуальный динамический анализ как четких (однозначно идентифицированных), так и нечетких (неоднозначно идентифицируемых) текущих состояний объекта с экрана многоцветного видеомонитора и оперативно (в реальном масштабе времени) определять относительную величину и характер изменения диагностируемого обобщенного состояния МПО с оценкой последовательности (предыстории) его изменения. Все это в комплексе обеспечивает сокращение сроков анализа состояния МПО и используемых технических средств отображения динамических параметров для информационной поддержки принятия решений экспертаманалитикам, подготавливающим решения по диагностике состояний МПО.
Способ оперативного динамического анализа нечеткого состояния МПО предлагается использовать в комплексе совместно со способом цветокодового представления и анализа динамики состояния многопараметрического объекта или процесса. Данное условие необходимо, так как результаты представления информации состояния МПО отображаются на экране многоцветового монитора посредством наглядного визуального представления всей обобщенной информации о МПО или определенной ее части в виде когнитивной цветокодовой матрицыдиаграммы.
При анализе состояния МПО, наблюдаемого по 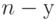 динамическому параметру (показателю состояния МПО), его текущее состояние в
динамическому параметру (показателю состояния МПО), его текущее состояние в  -й момент времени можно представить в виде выражения:
-й момент времени можно представить в виде выражения:
 |
( 8.1) |
где 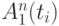 - штатное четкое состояние иго параметра, т. е. параметр однозначно находится в
- штатное четкое состояние иго параметра, т. е. параметр однозначно находится в 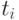 -й момент времени в допуске;
-й момент времени в допуске;
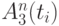 - нештатное четкое состояние
- нештатное четкое состояние  -го параметра, т. е. параметр однозначно находится в
-го параметра, т. е. параметр однозначно находится в 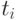 -й момент времени не в допуске;
-й момент времени не в допуске;
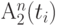 - нечеткое состояние
- нечеткое состояние  -го параметра, т. е. система обработки в
-го параметра, т. е. система обработки в 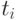 -й момент времени не может в силу тех или иных причин однозначно определить, в допуске или не в допуске динамический параметр.
-й момент времени не может в силу тех или иных причин однозначно определить, в допуске или не в допуске динамический параметр.
Нечеткость состояния параметра определяется тем, что его текущее значение ввиду размытости, расплывчатости может быть отнесено как к штатному, так и нештатному состоянию. Традиционное представление динамических параметров представлено на рис. 8.8. Цветокодовая матрицадиаграмма изменения состояния многопараметрического объекта или процесса представлена на рис. 8.9.
Обобщая выражение (8.1) по всему множеству динамических параметров 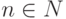 для МПО в целом, получаем возможные обобщенные оценки классов состояния:
для МПО в целом, получаем возможные обобщенные оценки классов состояния:
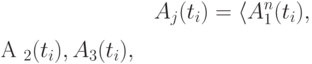 |
( 8.2) |
Состояние динамических параметров, оцененных в соответствии с выражением (8.2) по этапам функционирования объекта, определяет соответственно его обобщенное (интегральное) состояние и переходы объекта из одного состояния в другое (динамику состояний). Например, в простейшем случае множества 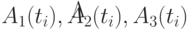 определяют соответствующие классы штатных
определяют соответствующие классы штатных 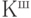 и нештатных
и нештатных 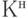 состояний МПО.
состояний МПО.
Очевидно, чем более неопределенней (неоднозначней) ситуация на выходе МПО и чем большее влияние оказывают различные дестабилизирующие факторы на динамический параметр, тем труднее провести оценку текущего нечеткого состояния МПО с идентификацией исходного многопараметрического пространства на классы 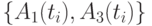 четких состояний динамических параметров и тем большее количество динамических параметров попадает в класс
четких состояний динамических параметров и тем большее количество динамических параметров попадает в класс 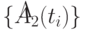 нечетких состояний.
нечетких состояний.
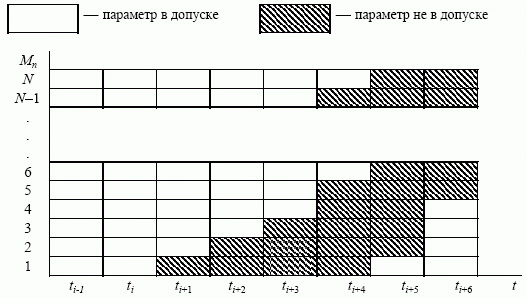
Рис. 8.9. Цветокодовая матрицадиаграмма изменения состояния многопараметрического объекта или процесса
Нечеткое подмножество 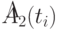 можно представить в виде соотношения:
можно представить в виде соотношения:
 |
( 8.3) |
где 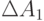 и
и  - значения погрешностей определения
- значения погрешностей определения 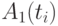 и
и  соответственно при оценке параметров из исходного множества
соответственно при оценке параметров из исходного множества 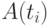 , которые не позволяют однозначно идентифицировать (классифицировать, распознать) анализируемый параметр и отнести его к одному из четких подмножеств
, которые не позволяют однозначно идентифицировать (классифицировать, распознать) анализируемый параметр и отнести его к одному из четких подмножеств 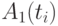 и
и  .
.
Исключение сложной операции идентификации (классификации, распознавания) нечетких состояний динамических параметров только на классы четких состояний (классы эквивалентности) и переход к гибкой классификации на базе введения класса нечеткого состояния (класса толерантности) динамического параметра позволяет значительно упростить процесс оперативной обработки и анализа нечетких состояний динамических параметров и нечеткого состояния МПО в целом.
Введем обобщенную характеристику:
 |
( 8.4) |
где  - общее количество динамических параметров,
- общее количество динамических параметров, 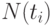 - количество динамических параметров, текущее значение которых в
- количество динамических параметров, текущее значение которых в 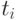 - момент времени отнесено к одному из подмножеств (классов)
- момент времени отнесено к одному из подмножеств (классов) 
Используя введенные характеристики (8.2) и (8.4), можно получать различные цветокодовые матрицы - гистограммы состояний МПО. Так, кодируя определенным цветовым кодом видимого спектра каждый из выделенных классов состояний (8.2) динамических параметров и представляя относительную величину 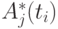 в виде информационного поля соответствующего подмножества динамических параметров, получаем трехуровневую цветокодовую матрицу - гистограмму состояния МПО (рис. 8.10).
в виде информационного поля соответствующего подмножества динамических параметров, получаем трехуровневую цветокодовую матрицу - гистограмму состояния МПО (рис. 8.10).
увеличить изображение
Рис. 8.10. Трехуровневая цветокодовая матрицагистограмма состояния многопараметрического объекта
Сущность способа состоит в том, что с целью обеспечения оперативного динамического анализа нечеткого состояния многопараметрического объекта или процесса проводится оперативное преобразование результатов допусковой оценки четких состояний разнородных динамических параметров в соответствующие информационные цветокодовые сигналы с обобщением по всему множеству динамических параметров в заданном временном интервале. В качестве показателей оцениваемой характеристики используют динамические параметры. В качестве результатов оценки используют результаты допусковой оценки нечетких состояний динамических параметров. Операцию преобразования осуществляют формированием соответствующего информационного цветокодового сигнала видимого спектра в зависимости от результатов допусковой оценки текущих состояний динамического параметра с последующим отнесением его к одному из классов четких или нечетких состояний (в допуске, не в допуске, не известно) с обобщением по всему множеству параметров на заданном интервале. Отображают информационные цветокодовые сигналы посредством трехуровневой матрицыгистограммы состояний. Ее столбцы соответствуют относительным величинам оцененных классов четких и нечетких состояний динамических параметров объекта, а строки - заданным временным интервалам. Определяют относительную величину и характер изменения интегрального состояния многопараметрического объекта по направлениям изменения и относительным величинам этого изменения во времени информационных цветокодовых сигналов.
Таким образом, нечеткое многопараметрическое пространство состояний всего множества (потока) динамических параметров, независимо от его мощности, можно представить на экране многоцветового видеомонитора (дисплея) в виде трехуровневой цветокодовой матрицыгистограммы состояний МПО ![[A_j^*(t_{i})\cdot t_{i}]](/sites/default/files/tex_cache/8747770aa20485f3d6dad41ea3966de5.png) , где
, где 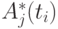 - относительное количество динамических параметров, принадлежащих
- относительное количество динамических параметров, принадлежащих 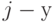 классу состояний,
классу состояний,  ,
, 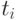 - время регистрации.
- время регистрации.
Новизна предлагаемого способа по сравнению с известными способами представления и анализа состояния многопараметрического объекта или процесса в том, что разработана логическая последовательность действий по представлению и анализу нечеткого состояния МПО. В основе такого подхода предлагается использовать новый подход к декомпозиции многопараметрического пространства нечетких состояний динамических параметров на классы четких и нечетких состояний, что значительно облегчает реализацию алгоритмов классификации (кластеризации) - распознавания (диагностики), идентификации и информационной поддержки принятия решений по управлению МПО.
Способ цветокодового представления и анализа динамики состояния многопараметрического объекта или системы. Для МПО трудность решения задач диагностики их состояний, изменяющихся во времени, обусловлена необходимостью оперативной оценки каждого динамического параметра, характеризующего функционирование МПО, на соответствующей циклограмме его работы в строгом соответствии со шкалой времени.
Способ цветокодового представления и анализа динамики состояния многопараметрического объекта или системы - универсальный способ цветокодового представления и анализа состояний сложных многопараметрических объектов на основе использования непрерывнодискретной шкалы переходов МПО из одного класса состояний в другой с учетом предыстории его функционирования, в составе которого положено оперативное выделение обобщенных цветокодовых описаний для информационной поддержки принятия решений.
Цель данного способа - оперативное представление и анализ изменения класса состояния многопараметрического объекта или системы, отображаемого множеством разнородных динамических параметров с определением последовательности, полноты и характера перехода его из одного состояния в другое.
Заявленная цель достигается реализацией способа цветокодового представления и анализа динамики состояния МПО за счет одновременной обработки и наглядного визуального представления всей обобщенной информации о МПО или определенной ее части в виде когнитивной цветокодовой матрицыдиаграммы состояния МПО. Осуществляется на основе перехода от традиционного представления динамического параметра в виде графика или функции изменения его значения во времени к нетрадиционному цветокодовому представлению динамики изменения текущего класса состояния МПО в виде матрицыдиаграммы. При этом каждый текущий класс состояния МПО определяется по всему множеству разнородных параметров и кодируется одним из цветов кода видимого спектра.
Способ, таким образом, позволяет обеспечить наглядное визуальное представление многомерного (многопараметрического) текущего состояния МПО на экране многоцветного видеомонитора и оперативно (в реальном масштабе времени) определять последовательность, полноту и характер перехода его из одного класса состояний в другой. Все это в комплексе обеспечивает сокращение сроков представления и визуального анализа динамической информации о состоянии МПО в различных прикладных областях деятельности и используемых технических средств ее отображения.
Сущность способа в том, что с целью обеспечения оперативного цветокодового представления и анализа состояния МПО, идентифицированные по допусковому способу, с точки зрения принадлежности к  -му классу состояния,
-му классу состояния, 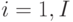 , текущие значения разнородных динамических параметров представляют в соответствующие информационные цветокодовые сигналы видимого спектра последовательно во времени с обобщением по всему множеству динамических параметров в заданном временном интервале. Операцию преобразования осуществляют формированием соответствующего информационного цветокодового сигнала. Информационные цветокодовые сигналы посредством матрицыдиаграммы состояния МПО. Ее столбцы соответствуют идентифицированному текущему значению
, текущие значения разнородных динамических параметров представляют в соответствующие информационные цветокодовые сигналы видимого спектра последовательно во времени с обобщением по всему множеству динамических параметров в заданном временном интервале. Операцию преобразования осуществляют формированием соответствующего информационного цветокодового сигнала. Информационные цветокодовые сигналы посредством матрицыдиаграммы состояния МПО. Ее столбцы соответствуют идентифицированному текущему значению  -го класса состояния динамического параметра, строки - заданным временным интервалам, определяют последовательность смены класса состояния МПО по циклограмме его наблюдаемых динамических параметров и
характер перехода (многопараметрического пространства пересечения классов) МПО из одного класса состояния в другой с обобщением по всему упорядоченному множеству разнородных динамических параметров, отображающих текущее состояние МПО.
-го класса состояния динамического параметра, строки - заданным временным интервалам, определяют последовательность смены класса состояния МПО по циклограмме его наблюдаемых динамических параметров и
характер перехода (многопараметрического пространства пересечения классов) МПО из одного класса состояния в другой с обобщением по всему упорядоченному множеству разнородных динамических параметров, отображающих текущее состояние МПО.
Предлагаемый способ позволяет оперативно определять последовательность, полноту и характер переходов МПО из одного класса состояния в другой по большому количеству (на порядок и более по сравнению с традиционным представлением) разнородных динамических параметров, что значительно облегчает восприятие общей интегральной картины смены состояния МПО.
Сущность предложенного способа проиллюстрируем для двухпараметрического пространства состояний МПО (рис. 8.11), где каждый динамический параметр 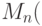 или
или 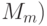 отображает в относительной величине одну из характеристик наблюдаемого МПО - амплитуду
отображает в относительной величине одну из характеристик наблюдаемого МПО - амплитуду 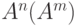 ее изменения. Очевидно, что с точки зрения оперативности принятия решения о переходе одного состояния МПО в другое крайне важна интегральная многопараметрическая характеристика его текущего состояния, несущая обобщенную информацию не столько количественного, сколько качественного (содержательного) характера. В качестве такой интегральной характеристики может быть использовано многопараметрическое пространство пересечения между классами состояния МПО.
ее изменения. Очевидно, что с точки зрения оперативности принятия решения о переходе одного состояния МПО в другое крайне важна интегральная многопараметрическая характеристика его текущего состояния, несущая обобщенную информацию не столько количественного, сколько качественного (содержательного) характера. В качестве такой интегральной характеристики может быть использовано многопараметрическое пространство пересечения между классами состояния МПО.
На рис. 8.11.а), б) приведено традиционное представление графиков изменения амплитуды динамических параметров МПО с установленными на нем измерительными датчиками 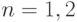 , которые формируют соответствующие динамические параметры. Переход двухпараметрического МПО из одного состояния в другое по
, которые формируют соответствующие динамические параметры. Переход двухпараметрического МПО из одного состояния в другое по 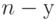 и
и  параметру в традиционной форме представления приведен на рис. 8.11 а), б), где участок АВ является областью перехода МПО из класса состояний
параметру в традиционной форме представления приведен на рис. 8.11 а), б), где участок АВ является областью перехода МПО из класса состояний  в класс
в класс 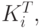 которая может быть различна для разных параметров. Очевидно, что классы
которая может быть различна для разных параметров. Очевидно, что классы 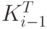 и
и 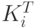 являются пересекающимися классами (классами толерантности). Анализ логики изменения динамических параметров на рассматриваемом участке времени позволяет определить крайние границы (
являются пересекающимися классами (классами толерантности). Анализ логики изменения динамических параметров на рассматриваемом участке времени позволяет определить крайние границы ( 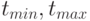 ) перехода объекта из состояния
) перехода объекта из состояния 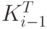 в состояние
в состояние 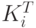 . Тогда
. Тогда  определим как временной интервал пространства этого перехода. Оно представляет собой некоторое множество пересечений
определим как временной интервал пространства этого перехода. Оно представляет собой некоторое множество пересечений 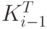 и
и 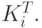 Проведем декомпозицию исходной ситуации на непересекающиеся классы (классы эквивалентности)
Проведем декомпозицию исходной ситуации на непересекающиеся классы (классы эквивалентности) 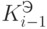 и
и 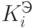 с выделением пространства пересечений
с выделением пространства пересечений
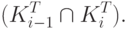
Определим частое пространство пересечений (перехода) МПО из состояния  в состояние
в состояние 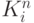 по
по 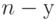 параметру в виде пересечения
параметру в виде пересечения  , тогда обобщенное по множеству
, тогда обобщенное по множеству  пространство
пространство 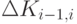 представим в виде:
представим в виде:
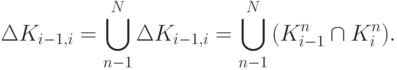 |
( 8.5) |
Полученное выражение (8.5), обобщенное по всему множеству наблюдаемых динамических параметров, может быть использовано для интегральной многопараметрической оценки факта изменения класса состояний, а следовательно, для распознавания состояний
МПО в динамике текущего времени. Построим матрицудиаграмму состояния МПО в виде некоторой координатной сетки, где по оси абсцисс отложено время (или определенные отрезки времени), а по оси ординат - веса заданных признаков (динамических параметров), несущих информацию о соответствующем классе состоянии МПО (рис. 8.11.в)). Кодируя определенным цветовым кодом видимого спектра каждый из классов по совокупности параметров, а также состояния перехода из одного класса состояний в другой для наглядности восприятия, получим обобщенное представление двухпараметрического пространства 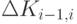 на момент смены состояний МПО в новой системе координат. С учетом предлагаемого подхода на рис. 8.11.в) приведено наглядное представление двух динамических параметров в виде многомерной цветокодовой матрицыдиаграммы
на момент смены состояний МПО в новой системе координат. С учетом предлагаемого подхода на рис. 8.11.в) приведено наглядное представление двух динамических параметров в виде многомерной цветокодовой матрицыдиаграммы ![[M_{n}(t_i)\cdot ti]](/sites/default/files/tex_cache/4832af2d5197fd764a1a916586de5ece.png) , где
, где 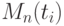 - упорядоченная совокупность информационных сигналов (полей) динамических параметров, в каждом из которых представляется последовательно во времени цветокодовая информация видимого спектра, соответствующая определенному текущему классу состояния МПО,
- упорядоченная совокупность информационных сигналов (полей) динамических параметров, в каждом из которых представляется последовательно во времени цветокодовая информация видимого спектра, соответствующая определенному текущему классу состояния МПО, 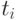 - характерные временные или пространственные координаты.
- характерные временные или пространственные координаты.
Выбор характеристики (показателя) изменения динамического параметра, диапазонов ее представления, шкалы цветокодирования и задания нужной гаммы цветов осуществляется оператороманалитиком по его желанию в зависимости от характера и особенностей решаемой задачи. Выбранный диапазон представления рассматриваемой характеристики динамического параметра с точки зрения принадлежности к  -му классу должен однозначно соответствовать (автоматически подстраиваться) выбранной шкале цветокодирования, соответствующей идентифицированному текущему классу состояний МПО, таким образом, чтобы каждому классу соответствовал строго определенный цвет шкалы цветокодирования.
-му классу должен однозначно соответствовать (автоматически подстраиваться) выбранной шкале цветокодирования, соответствующей идентифицированному текущему классу состояний МПО, таким образом, чтобы каждому классу соответствовал строго определенный цвет шкалы цветокодирования.
Визуальный анализ рассматриваемых представлений, раскрывающих суть предлагаемого способа, позволяет оперативно определять последовательность, полноту и характер смены текущего класса состояний МПО, наблюдаемого по каждому динамическому параметру и в целом по всему множеству динамических параметров МПО, в том числе:
- визуально оценить последовательность перехода по любой группе динамических параметров МПО в целом на исследуемых временных интервалах. Например, переход МПО из класса состояний
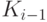 в класс
в класс 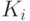 наглядно представляется цветокодовой матрицей диаграммой по любому множеству динамических параметров, фиксирующих динамические изменения той или иной характеристики;
наглядно представляется цветокодовой матрицей диаграммой по любому множеству динамических параметров, фиксирующих динамические изменения той или иной характеристики; - оценить характер многопараметрического пространства перехода МПО из одного класса состояния в другой на рассматриваемом интервале времени.
Таким образом, способ обеспечивает оперативное представление и анализ текущего состояния МПО с определением последовательности, полноты и характера перехода его из одного состояния в другое по всему множеству разнородных динамических параметров. Все это в комплексе обеспечивает сокращение сроков обработки и анализа информации и используемых технических средств ее отображения для информационной поддержки принятия решений.
Предложенный подход дает наглядные модели состояний МПО в виде некоторой логической совокупности цветокодовых матриц-диаграмм состояний МПО.
Динамический просмотр таких совокупностей по реальной информации в режиме мониторинга на анализируемом интервале времени позволяет:
- отслеживать, находить, выявлять на визуальном уровне главные тенденции в поведении (изменении свойств) МПО;
- оперативно идентифицировать переходы объекта из одного состояния в другое, оценивать общую картину динамики изменения его состояния по всей циклограмме его функционирования;
- использовать человекаоператора в качестве окончательного элемента системы анализа, так как он может наблюдать на экране одного или нескольких многоцветных видеомониторов необходимые для ИППР по диагностике состояний МПО обобщенные данные обо всем потоке поступающей динамической информации, в том числе информации о различных (разнотипных) параметрах (показателей), которую невозможно анализировать на одном информационном поле при традиционном представлении;
- обеспечить формализацию процесса диагностирования за счет многомерного представления и визуализации нечетких обобщенных данных. Его особенность в том, что априорными описаниями классов являются структурные описания - цветокодовые представления, рассматриваемые последовательно по времени функционирования МПО, при получении которых проводится принцип учета последовательности изменения классов состояний МПО (структуры) и учета отношений, существующих между отдельными элементами анализируемых представлений;
- исключить ряд наиболее трудоемких "ручных" операций, таких, как: непрерывный контроль характера изменения функциональных параметров, оперативная оценка поля допуска по каждому параметру в условиях помех и искажений, проведение обобщения по всем параметрам, несущим информацию о состоянии МПО.
Представление параметров, признаков или показателей. Традиционно результаты эксперимента или наблюдений (эмпирические данные) представляются в виде матрицы данных, в основе которой описаны параметры, признаки или показатели, характеризующие состояние исследуемого объекта или процесса.
Пусть сложный объект или процесс характеризуется некоторым конечным множеством параметров, признаков или показателей. Каждый из них описывается некоторым множеством характеристик. В общем случае считаем, что параметры, признаки, показатели и их характеристики находятся в функциональной зависимости от времени и соответственно характеризуют текущее состояние динамического объекта или процесса. Будем считать, что сложноорганизованная информация представлена в виде некоторого многопараметрического (  -мерного) пространства измерений. Его оси соответствуют отдельным параметрам, а каждую строку матрицы данных рассматриваем как вектор в этом пространстве.
-мерного) пространства измерений. Его оси соответствуют отдельным параметрам, а каждую строку матрицы данных рассматриваем как вектор в этом пространстве.
Текущее состояние параметра, признака или показателя, описывающее состояние сложного объекта или процесса, в общем случае может характеризоваться некоторым набором характеристик. В каждом параметре (признаке, показателе) можно выделить информационные, структурные и идентифицирующие характеристики.
Пусть состояние  -го динамического параметра (показателя, коэффициента)
-го динамического параметра (показателя, коэффициента) 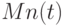 сложного многомерного (многопараметрического) объекта или процесса характеризуется совокупностью
сложного многомерного (многопараметрического) объекта или процесса характеризуется совокупностью 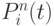 частных информационных характеристик:
частных информационных характеристик:
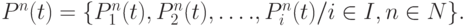
Среди которых выделим основные:
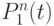 - факт выхода параметра за допустимое поле допуска;
- факт выхода параметра за допустимое поле допуска;
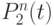 - амплитуда изменения параметра в физической или относительной величине;
- амплитуда изменения параметра в физической или относительной величине;
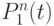 - принадлежность значения параметра определенному классу состояний многопараметрического объекта.
- принадлежность значения параметра определенному классу состояний многопараметрического объекта.
Состояние  -го динамического параметра
-го динамического параметра 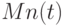 сложного многопараметрического объекта или процесса представляем в виде:
сложного многопараметрического объекта или процесса представляем в виде:
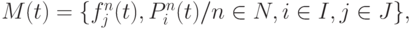
где 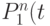 ) -
) -  -й показатель (характеристика) состояния
-й показатель (характеристика) состояния  -го параметра, а
-го параметра, а
 -
-  -я форма его описания.
-я форма его описания.
Состояние  -го динамического параметра
-го динамического параметра 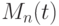 сложного многопараметрического объекта или процесса может быть отображено совокупностью различных форм представления:
сложного многопараметрического объекта или процесса может быть отображено совокупностью различных форм представления:
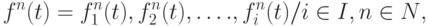
где 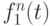 -
-  -я форма представления состояния динамического параметра. (табличная, графическая, цветовая форма представления и т. п.).
-я форма представления состояния динамического параметра. (табличная, графическая, цветовая форма представления и т. п.).
Соответственно, состояние всех наблюдаемых динамических параметров на  -й момент времени характеризует многомерное (многопараметрическое) текущее состояние сложного объекта или процесса по
-й момент времени характеризует многомерное (многопараметрическое) текущее состояние сложного объекта или процесса по  -му показателю и
-му показателю и  -й форме его представления.
-й форме его представления.
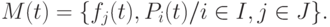
Принцип цветокодирования по степени принадлежности заданному полю допуска. При обработке и анализе сложноорганизованной информации часто приходится осуществлять оценку принадлежности (принадлежит, не принадлежит) или степени принадлежности (с каким значением принадлежности) нечетких значений параметра заданному полю допуска, классу состояний.
Рассмотрим подход к визуализации процесса динамической оценки степени принадлежности заданному полю допуска текущих значений параметра.
Полагаем, что оценка состояния произвольного  -го параметра
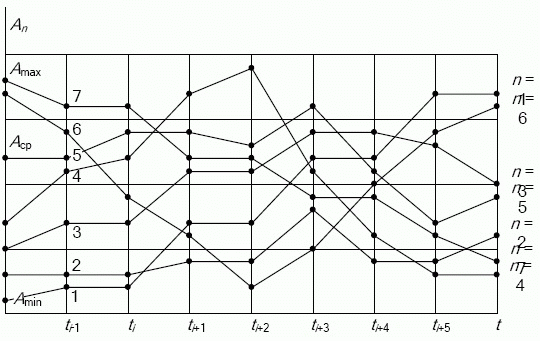
-го параметра 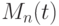 проводится по степени принадлежности его текущих значений заданному полю допуска во времени по циклограмме функционирования исследуемого объекта или процесса. Тогда состояние рассматриваемого объекта или процесса относительно данного параметра можно представить в виде:
проводится по степени принадлежности его текущих значений заданному полю допуска во времени по циклограмме функционирования исследуемого объекта или процесса. Тогда состояние рассматриваемого объекта или процесса относительно данного параметра можно представить в виде:
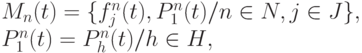
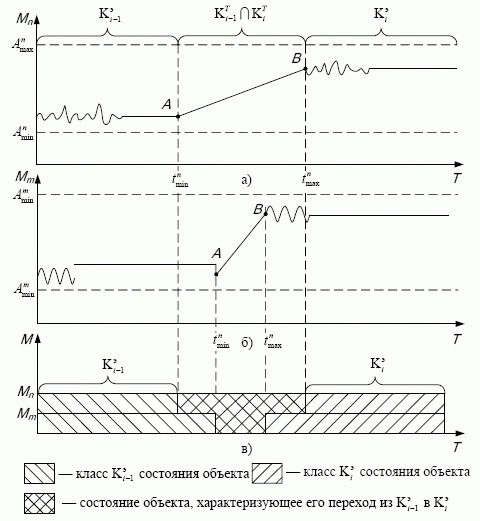
где 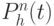 - принадлежность значения параметра заданному полю допуска по оцениваемой
- принадлежность значения параметра заданному полю допуска по оцениваемой  -й характеристике.
-й характеристике.
Сущность такого цветокодирования в том, что текущее значение анализируемой характеристики динамического параметра в зависимости от степени принадлежности его текущих значений заданному полю допуска кодируется определенным кодом видимого спектра и представляется соответствующей цветокодовой ячейкой. Каждая ячейка соответствует определенному значению степени принадлежности значения параметра (характеристики) заданному полю допуска. Это достигается путем перехода от представления параметра в виде графика или функции изменения его значения во времени к цветокодовому представлению факта выхода за поле допуска текущего значения параметра исследуемого объекта, при этом проводится обобщение по множеству параметров одним из цветов кода видимого спектра.
Построение интегрального показателя оценки организационно-экономической устойчивости предприятия. При формировании интегрального показателя организационно-экономической устойчивости предприятия можно использовать довольно много расчетных показателей и коэффициентов. Важно, чтобы выбранные для анализа показатели:
- несли конкретный смысл, отражая основные грани работоспособности и устойчивости предприятия как сложной системы (т. е. грани ее функционального состояния);
- можно было выразить в относительных величинах. Последнее условие необходимо для построения именно интегрального показателя, отражающего состояние системы в целом и формирующегося с учетом состояния показателей устойчивости всех подсистем в совокупности, т. е. зависящего от локальных показателей устойчивости.
На основании разработанной системы классификации показателей и подхода к формированию интегрального показателя организационно-экономической устойчивости предприятия предлагается следующая схема построения этого показателя.
- На основе представленной классификации показателей, характеризующих организационно-экономическую устойчивость предприятия, выделяются ключевые параметры в каждом из определенных блоков параметров функционирования той или иной системы предприятия (табл. 8.2.).
- На основании экономико-математических расчетов, представленных в подходе к формированию интегрального показателя организационно-экономической устойчивости предприятия, определяются локальные показатели устойчивости по каждому из блоков каждой из систем предприятия, производственно-сбытовой и финансово-экономической.
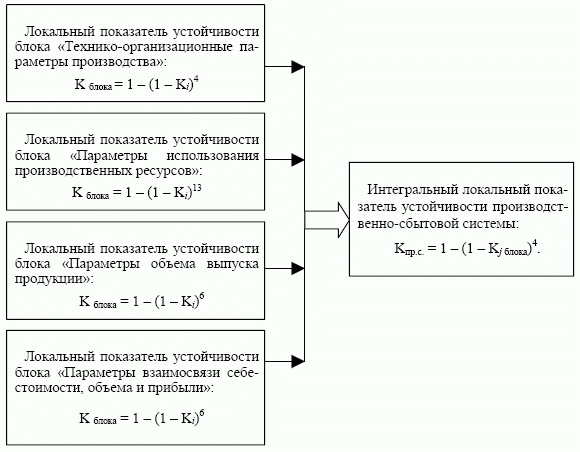
Схема расчета локального показателя устойчивости блока представлена на примере расчета локального показателя устойчивости блока: "Технико-организационные параметры производства" (рис. 8.12).
увеличить изображение
Рис. 8.12. Схема расчета локального показателя устойчивости блока "Технико-организационные параметры производства" - Производится расчет локальных интегральных показателей по производственно-сбытовой и финансово-экономической системам. Схема расчета интегрального показателя устойчивости производственно-сбытовой системы представлена на рис. 8.13.
- Определяется интегральный показатель организационно-экономической устойчивости по предприятию в целом.
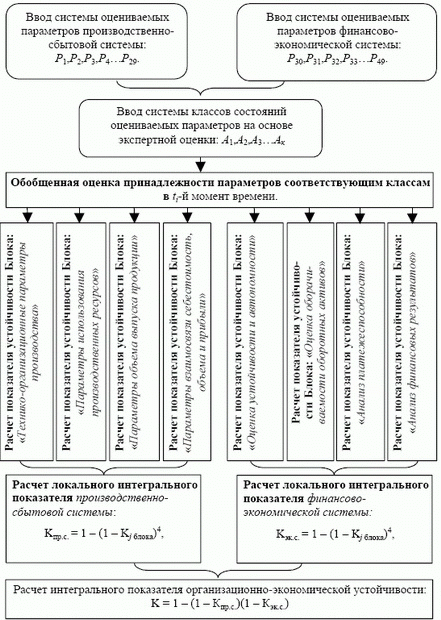
Схема построения интегрального показателя организационно-экономической устойчивости представлена на рис. 8.14.
увеличить изображение
Рис. 8.14. Схема построения интегрального показателя организационно-экономической устойчивости
Сформированный показатель интегральной оценки организационно-экономического состояния предприятия отвечает всем задачам и целям (на уровне оперативного анализа), оценке эффективности деятельности предприятия как многопараметрического объекта с множеством взаимосвязей с внешней средой функционирования. Данный показатель отражает важнейшую характеристику состояния устойчивости предприятия в целом: организационно-экономическая устойчивость может быть достигнута исключительно при параллельном сочетании производственно-сбытовой и финансово-экономической устойчивости.



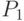 - анализ ритмичности;
- анализ ритмичности; - анализ комплектности;
- анализ комплектности;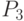 - анализ выполнения плана по номенклатуре;
- анализ выполнения плана по номенклатуре;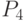 - анализ незавершенного производства.
- анализ незавершенного производства.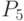 - трудовые ресурсы;
- трудовые ресурсы;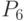 - производительность труда;
- производительность труда;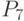 - среднегодовая стоимость основных средств;
- среднегодовая стоимость основных средств;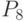 - степень износа;
- степень износа;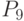 - готовность основных средств;
- готовность основных средств; - обновление основных средств;
- обновление основных средств;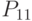 - выбытие основных средств;
- выбытие основных средств; - фондовооруженность;
- фондовооруженность;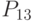 - энерговооруженность;
- энерговооруженность; - фондоотдача;
- фондоотдача;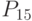 - материалоемкость продукции;
- материалоемкость продукции;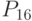 - обеспеченность запасами;
- обеспеченность запасами;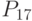 - соблюдение нормы расходов.
- соблюдение нормы расходов.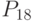 -
- 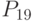 - фактические объемы производства по
- фактические объемы производства по 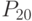 - фактические объемы реализации по
- фактические объемы реализации по 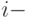 му виду продукции
му виду продукции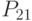 - максимально возможные объемы производства по
- максимально возможные объемы производства по 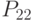 - максимально возможные объемы по факту наблюдения за рынком реализации по
- максимально возможные объемы по факту наблюдения за рынком реализации по 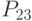 - планируемые объемы реализации по
- планируемые объемы реализации по 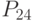 - взаимосвязь между выручкой, издержками и прибылью;
- взаимосвязь между выручкой, издержками и прибылью;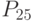 - объем продаж в натуральном выражении;
- объем продаж в натуральном выражении;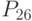 - объем продаж в денежном выражении;
- объем продаж в денежном выражении; - предельный уровень цены товара;
- предельный уровень цены товара;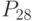 - необходимый объем выручки для обеспечения заданной прибыли;
- необходимый объем выручки для обеспечения заданной прибыли; _{29} - предельный допустимый уровень переменных издержек при заданных параметрах цен, прибыли, либо условно-постоянных затрат.
_{29} - предельный допустимый уровень переменных издержек при заданных параметрах цен, прибыли, либо условно-постоянных затрат.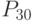 - автономность;
- автономность;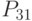 - финансовая устойчивость,
- финансовая устойчивость,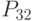 - обеспеченность собственными оборотными средствами;
- обеспеченность собственными оборотными средствами;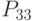 - маневренность;
- маневренность; - инвестирования.
- инвестирования.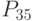 - оборачиваемость
- оборачиваемость 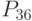 - оборачиваемость запасов;
- оборачиваемость запасов;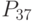 - оборачиваемость дебиторской задолженности;
- оборачиваемость дебиторской задолженности;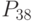 - достаточность денежных средств;
- достаточность денежных средств;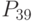 - период предпринимательского кредита.
- период предпринимательского кредита.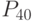 - абсолютная ликвидность;
- абсолютная ликвидность; - ликвидность;
- ликвидность; - текущая ликвидность.
- текущая ликвидность.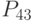 - рентабельность
- рентабельность 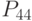 - рентабельность акционерного капитала;
- рентабельность акционерного капитала; - рентабельность инвестиционного капитала;
- рентабельность инвестиционного капитала;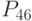 - рентабельность активов;
- рентабельность активов;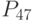 - рентабельность
- рентабельность 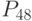 - рентабельность продаж;
- рентабельность продаж;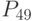 - рентабельность продукции.
- рентабельность продукции.