| ВКР |
Управление организационно-экономической устойчивостью промышленных корпоративных систем на основе динамического анализа состояния в условиях неопределенности
8.5. Общая схема изучения устойчивости в математических моделях организационно-экономических явлений и процессов
Понятие "организационно-экономическая устойчивость предприятия". Понятие "устойчивость" пришло в экономическую науку из математики, где изначально имело следующее значение (определение А.М. Ляпунова).
Определение. Система устойчива, если

т. е. если малым возмущениям внешней системы соответствуют малые возмущения рассматриваемой системы, то такая система считается устойчивой.
В экономике понятие организационно-экономической устойчивости предприятия введено следующим образом:
" … способность сохранять финансовую стабильность предприятия при постоянном изменении рыночной конъюнктуры путем совершенствования и целенаправленного развития его производственнотехнологической и организационной структуры … " [1]
Таким образом, стремление сохранять свое положение на рынке подразумевает комплекс мер по поддержанию стабильного положения предприятия под воздействием внешней среды, т. е. создание системы управления, отслеживающей изменения внешней системы и обеспечивающей выработку управляющих воздействий, поддерживающих предприятие на желательном уровне развития.
Целесообразно рассмотреть общее представление об устойчивости, сложившееся в современной науке.
Устойчивость математических моделей. Проблемам познания, в том числе в технических исследованиях, естественнонаучных и социальноэкономических областях, посвящено огромное количество работ. Однако это не значит, что обо всем в этой области уже все сказано. А о некоторых положениях целесообразно говорить еще и еще раз, пока они не станут общеизвестными.
В идеале каждую модель порождения и анализа данных следовало бы рассматривать как аксиоматическую теорию. В этом идеальном случае создание и использование модели происходит в соответствии с известной триадой "практика - теория - практика". А именно, сначала вводятся некоторые математические объекты, соответствующие интересующим исследователя реальным объектам, и на основе представлений о свойствах реальных объектов формулируются необходимые для успешного моделирования свойства математических объектов, которые и принимаются в качестве аксиом. Затем аксиоматическая теория развивается как часть математики, вне связи с представлениями о реальных объектах. На заключительном этапе полученные в математической теории результаты интерпретируются содержательно. Получаются утверждения о реальных объектах, являющиеся следствиями тех и только тех их свойств, которые ранее были аксиоматизированы.
После построения математической модели реального явления или процесса встает вопрос об ее адекватности. Иногда ответ на этот вопрос может дать эксперимент. Рассогласование модельных и экспериментальных данных следует интерпретировать как признак неадекватности некоторых из принятых аксиом. Однако для проверки адекватности социальноэкономических моделей зачастую невозможно поставить решающий эксперимент в отличие, скажем, от физических моделей. С другой стороны, для одного и того же явления или процесса, как правило, можно составить много возможных моделей, если угодно, много разновидностей одной базовой модели. Поэтому необходимы какието дополнительные условия, позволяющие из множества возможных моделей и эконометрических методов анализа данных выбрать наиболее подходящие. В качестве одного из подобных условий выдвигается требование устойчивости модели и метода анализа данных относительно допустимых отклонений исходных данных и предпосылок модели или условий применимости метода.
В большинстве случаев исследователей и практических работников интересуют не столько сами модели и методы, сколько решения, которые с их помощью принимаются. Ведь модели и методы для того и разрабатываются, чтобы подготавливать решения. Вместе с тем очевидно, что решения, как правило, принимаются в условиях неполноты информации. Так, любые числовые параметры известны лишь с некоторой точностью. Введение в рассмотрение возможных неопределенностей исходных данных требует какихто заключений относительно устойчивости принимаемых решений по отношению к этим допустимым неопределенностям.
Введем основные понятия согласно монографии [16]. Будем считать, что имеются исходные данные, на основе которых принимаются решения. Способ переработки (отображения) исходных данных в решение назовем моделью. С общей точки зрения модель - это функция, переводящая исходные данные в решение, т. е. способ перехода значения не имеет. Очевидно, любая рекомендуемая для практического использования модель должна быть исследована на устойчивость относительно допустимых отклонений исходных данных. Укажем некоторые возможные применения результатов подобного исследования:
- заказчик научноисследовательской работы получает представление о точности предлагаемого решения;
- удается выбрать из многих моделей наиболее адекватную;
- по известной точности определения отдельных параметров модели удается указать необходимую точность нахождения остальных параметров;
- переход к случаю "общего положения" позволяет получать более сильные с математической точки зрения результаты.
Примеры. По каждому из четырех перечисленных возможных применений в [16, 18] приведены различные примеры. В прикладной статистике точность предлагаемого решения связана с разбросом исходных данных и с объемом выборки. Выбору наиболее адекватной модели посвящены многие рассмотрения в монографии по прикладной статистике [19], связанные с обсуждением моделей однородности и регрессии. Использование рационального объема выборки в статистике интервальных данных исходит из принципа уравнивания погрешностей. Этот принцип основан на том, что по известной точности определения отдельных параметров модели удается указать необходимую точность нахождения остальных параметров. Другой пример применения принципа уравнивания погрешностей - нахождение необходимой точности оценивания параметров в моделях логистики, рассмотренных в главе 5 монографии [16]. Наконец, переходом к случаю "общего положения" в прикладной статистике является переход к непараметрическим методам. Он необходим из-за невозможности обосновать принадлежность результатов наблюдений к тем или иным параметрическим семействам.
Специалисты по математическому моделированию и теории управления считают устойчивость одной из важных характеристик технических, социальноэкономических, медицинских и иных моделей. Достаточно глубокие исследования ведутся по ряду направлений.
Первоначальное изучение влияния малого изменения одного параметра обычно называют анализом чувствительности. Оно описывается значением частной производной. Если модель задается дифференцируемой функцией, итог анализа чувствительности - вектор значений частных производных в анализируемой точке.
Теория устойчивости решений дифференциальных уравнений развивается по крайней мере с XIX в. [20]. Выработаны соответствующие понятия - устойчивость по Ляпунову, корректность, доказаны глубокие теоремы. Для решения некорректных задач академиком АН СССР А.Н. Тихоновым в начале 1960-х гг. предложен метод регуляризации. Модели явлений и процессов, выражаемые с помощью дифференциальных уравнений, могут быть исследованы на устойчивость путем применения хорошо разработанного математического аппарата.
Вопросы устойчивости изучались практически во всех направлениях прикладных математических методов - и в математическом программировании, и в теории массового обслуживания (теории очередей), и в экологоэкономических моделях, и в различных областях эконометрики.
Общая схема устойчивости. Прежде чем переходить к конкретным постановкам, обсудим "общую схему устойчивости", дающую понятийную базу для обсуждения проблем устойчивости в различных предметных областях.
Определение 1. Общей схемой устойчивости называется объект 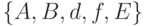 .
.
Здесь  - множество, интерпретируемое как пространство исходных данных;
- множество, интерпретируемое как пространство исходных данных;  - множество, называемое пространством решений. Однозначное отображение
- множество, называемое пространством решений. Однозначное отображение 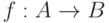 называется моделью. Об этих трех составляющих общей схемы устойчивости уже шла речь выше.
называется моделью. Об этих трех составляющих общей схемы устойчивости уже шла речь выше.
Оставшиеся два понятия нужны для уточнения понятий близости в пространстве исходных данных и пространстве решений. Подобные уточнения могут быть сделаны разными способами. Самое "слабое" уточнение - на языке топологических пространств. Тогда возможны качественные выводы (сходится - не сходится), но не количественные расчеты. Самое "сильное" уточнение - на языке метрических пространств. Промежуточный вариант - используются показатели различия (отличаются от метрик тем, что необязательно выполняются неравенства треугольника) или вводимые ниже понятия.
Пусть  -показатель устойчивости, т. е. неотрицательная функция, определенная на подмножествах
-показатель устойчивости, т. е. неотрицательная функция, определенная на подмножествах  множества
множества  и такая, что из
и такая, что из  вытекает
вытекает 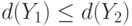 . Часто показатель устойчивости
. Часто показатель устойчивости 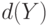 определяется с помощью метрики, псевдометрики или показателя различия (меры близости)
определяется с помощью метрики, псевдометрики или показателя различия (меры близости)  как диаметр множества
как диаметр множества  , т. е.
, т. е.
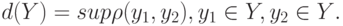
Таким образом, говоря попросту, в пространстве решений с помощью показателя устойчивости вокруг образа исходных данных может быть сформирована система окрестностей. Но сначала надо такую систему сформировать в пространстве исходных данных.
Пусть 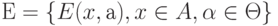 - совокупность допустимых отклонений. Т. е. система подмножеств множества
- совокупность допустимых отклонений. Т. е. система подмножеств множества  такая, что каждому элементу множества исходных данных
такая, что каждому элементу множества исходных данных 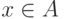 и каждому значению параметра а из некоторого множества параметров
и каждому значению параметра а из некоторого множества параметров  соответствует подмножество
соответствует подмножество 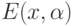 множества исходных данных. Оно называется множеством допустимых отклонений в точке
множества исходных данных. Оно называется множеством допустимых отклонений в точке  при значении параметра, равном а . Наглядно можно представить себе, что вокруг точки
при значении параметра, равном а . Наглядно можно представить себе, что вокруг точки  взята окрестность радиуса
взята окрестность радиуса 
Определение 2. Показателем устойчивости в точке  при значении параметра, равном
при значении параметра, равном  , называется число
, называется число
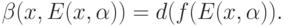
Другими словами, это - диаметр образа множества допустимых колебаний при рассматриваемом в качестве модели отображении. Очевидно, что этот показатель устойчивости зависит как от исходных данных, так и от диаметра множества возможных отклонений в исходном пространстве. Для непрерывных функций показатель устойчивости обычно называется модулем непрерывности.
Естественно посмотреть, насколько сузится образ окрестности возможных отклонений при максимально возможном сужении этой окрестности.
Определение 3. Абсолютным показателем устойчивости в точке х называется число

Если функция  непрерывна, а окрестности - именно те, о которых идет речь в математическом анализе, то максимальное сужение означает сужение к точке и абсолютный показатель устойчивости равен 0. Но в теории измерений и статистике интервальных данных мы сталкиваемся с совсем иными ситуациями. В теории измерений окрестностью исходных данных являются все те вектора, что получаются из исходного путем преобразования координат с помощью допустимого преобразования шкалы, а допустимое преобразование шкалы берется из соответствующей группы допустимых преобразований. В статистике интервальных данных под окрестностью исходных данных естественно понимать - при описании выборки - куб с ребрами
непрерывна, а окрестности - именно те, о которых идет речь в математическом анализе, то максимальное сужение означает сужение к точке и абсолютный показатель устойчивости равен 0. Но в теории измерений и статистике интервальных данных мы сталкиваемся с совсем иными ситуациями. В теории измерений окрестностью исходных данных являются все те вектора, что получаются из исходного путем преобразования координат с помощью допустимого преобразования шкалы, а допустимое преобразование шкалы берется из соответствующей группы допустимых преобразований. В статистике интервальных данных под окрестностью исходных данных естественно понимать - при описании выборки - куб с ребрами 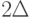 и центром в исходном векторе. И в том, и в другом случае максимальное сужение не означает сужение к точке.
и центром в исходном векторе. И в том, и в другом случае максимальное сужение не означает сужение к точке.
Естественным является желание ввести характеристики устойчивости на всем пространстве. Не вдаваясь в математические тонкости (см. о них монографию [16]), рассмотрим меру  на пространстве
на пространстве  такую, что мера всего пространства равна 1 (т. е.
такую, что мера всего пространства равна 1 (т. е. 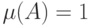 ).
).
Определение 4. Абсолютным показателем устойчивости на пространстве исходных данных  по мере
по мере  называется число
называется число
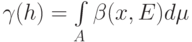
Здесь имеется в виду интеграл Лебега. Интегрирование проводится по (абстрактному) пространству исходных данных  по мере
по мере  . Естественно, должны быть выполнены некоторые внутриматематические условия. Читателю, не знакомому с интегрированием по Лебегу, достаточно мысленно заменить в предыдущей формуле интеграл на сумму (а пространство
. Естественно, должны быть выполнены некоторые внутриматематические условия. Читателю, не знакомому с интегрированием по Лебегу, достаточно мысленно заменить в предыдущей формуле интеграл на сумму (а пространство  считать конечным, хотя и состоящим из большого числа элементов).
считать конечным, хотя и состоящим из большого числа элементов).
Определение 5. Максимальным абсолютным показателем устойчивости называется
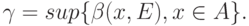
Легко видеть, что  , где супремум берется по всем описанным выше мерам.
, где супремум берется по всем описанным выше мерам.
Итак, построена иерархия показателей устойчивости математических моделей реальных явлений и процессов. Она с успехом использовалась в различных исследованиях, подробно развивалась, в частности, в монографии [16]. Приведем еще одно полезное определение.
Определение 6. Модель  называется абсолютно
называется абсолютно  -устойчивой, если
-устойчивой, если  , где
, где  - максимальный абсолютный показатель устойчивости.
- максимальный абсолютный показатель устойчивости.
Пример. Если показатель устойчивости формируется с помощью метрики  , совокупность допустимых отклонений
, совокупность допустимых отклонений  - это совокупность всех окрестностей всех точек пространства исходных данных
- это совокупность всех окрестностей всех точек пространства исходных данных 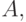 то 0-устойчивость модели
то 0-устойчивость модели  эквивалентна непрерывности модели
эквивалентна непрерывности модели  на множестве
на множестве  .
.
Основная проблема в общей схеме устойчивости - проверка  -устойчивости данной модели
-устойчивости данной модели  относительно данной системы допустимых отклонений
относительно данной системы допустимых отклонений  .
.
Часто оказываются полезными следующие два обобщения основной проблемы.
Проблема А (характеризации устойчивых моделей). Даны пространство исходных данных 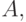 пространство решений
пространство решений  , показатель устойчивости
, показатель устойчивости  , совокупность допустимых отклонений
, совокупность допустимых отклонений  и неотрицательное число
и неотрицательное число  . Описать достаточно широкий класс
. Описать достаточно широкий класс  -устойчивых моделей
-устойчивых моделей 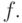 Или: найти все
Или: найти все  устойчивые модели среди моделей, обладающих данными свойствами, т. е. входящих в данное множество моделей.
устойчивые модели среди моделей, обладающих данными свойствами, т. е. входящих в данное множество моделей.
Проблема Б (характеризации систем допустимых отклонений). Даны пространство исходных данных 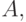 пространство решений
пространство решений  , показатель устойчивости
, показатель устойчивости  , модель
, модель  и неотрицательное число
и неотрицательное число  . Описать достаточно широкий класс систем допустимых отклонений
. Описать достаточно широкий класс систем допустимых отклонений  , относительно которых модель
, относительно которых модель  является
является  -устойчивой. Или: найти все такие системы допустимых отклонений
-устойчивой. Или: найти все такие системы допустимых отклонений  среди совокупностей допустимых отклонений, обладающих данными свойствами, т. е. входящих в данное множество совокупностей допустимых отклонений.
среди совокупностей допустимых отклонений, обладающих данными свойствами, т. е. входящих в данное множество совокупностей допустимых отклонений.
Ясно, что проблемы А и Б можно рассматривать не только для показателя устойчивости  , но и для других только что введенных показателей устойчивости, а именно,
, но и для других только что введенных показателей устойчивости, а именно,
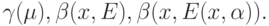
Язык общей схемы устойчивости позволяет описывать конкретные задачи специализированных теорий устойчивости в различных областях исследований, выделять основные элементы в них, ставить проблемы типа А и Б. В частности, на этом языке легко формулируются задачи теории устойчивости решений дифференциальных уравнений, теории робастности статистических процедур, проблемы адекватности теории измерений, достигаемой точности расчетов в статистике интервальных данных и в логистике (см. монографию [16]), и т. д.
Для примера рассмотрим определение устойчивости по Ляпунову решения 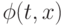 нормальной автономной системы дифференциальных уравнений
нормальной автономной системы дифференциальных уравнений 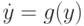 с начальными условиями
с начальными условиями 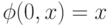 . Здесь пространство исходных данных
. Здесь пространство исходных данных  - конечномерное евклидово пространство, множество допустимых отклонений
- конечномерное евклидово пространство, множество допустимых отклонений  - окрестность радиуса
- окрестность радиуса  точки
точки 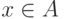 , пространство решений
, пространство решений  - множество функций на луче
- множество функций на луче 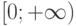 с метрикой
с метрикой
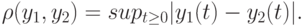 |
( t )|) |
Модель  - отображение, переводящее начальные условия
- отображение, переводящее начальные условия  в решение системы дифференциальных уравнений с этими начальными условиями
в решение системы дифференциальных уравнений с этими начальными условиями  .
.
В терминах общей схемы устойчивости положение равновесия  называется устойчивым по Ляпунову, если
называется устойчивым по Ляпунову, если  . Для формулировки определения асимптотической устойчивости по Ляпунову надо ввести в пространстве решений
. Для формулировки определения асимптотической устойчивости по Ляпунову надо ввести в пространстве решений  псевдометрику
псевдометрику
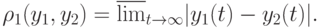 |
( t )|) |
Положение равновесия  называется асимптотически устойчивым, если
называется асимптотически устойчивым, если  для некоторого
для некоторого  , где показатель устойчивости
, где показатель устойчивости  рассчитан с использованием псевдометрики
рассчитан с использованием псевдометрики 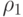 .
.
Таким образом, общая схема устойчивости естественным образом включает в себя классические понятия теории устойчивости по Ляпунову. Вместе с тем стоит отметить, что эта схема дает общий подход к различным проблемам устойчивости. Она дает систему понятий, которые в каждом конкретном случае должны приспосабливаться к решаемой задаче.
До настоящего момента для определенности речь шла о допустимых отклонениях в пространстве исходных данных. Часто оказывается необходимым говорить и об отклонениях от предпосылок модели. С чисто формальной точки зрения для этого достаточно расширить понятие "исходные данные" до пары 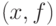 , т. е. включив "прежнюю" модель в качестве второго элемента пары. Все остальные определения остаются без изменения. Теперь отклонения в пространстве решений вызываются не только отклонениями в исходных данных
, т. е. включив "прежнюю" модель в качестве второго элемента пары. Все остальные определения остаются без изменения. Теперь отклонения в пространстве решений вызываются не только отклонениями в исходных данных  , но и отклонениями от предпосылок модели, т. е. отклонениями
, но и отклонениями от предпосылок модели, т. е. отклонениями  .
.
Устойчивость по отношению к объему выборки. Различные асимптотические постановки в прикладной статистике также естественно рассматривать как задачи устойчивости. Если при безграничном возрастании объема выборки некоторая величина стремится к пределу, то в терминах общей схемы устойчивости это означает, что она 0-устойчива в соответствующей псевдометрике (см. выше обсуждение асимптотической устойчивости по Ляпунову). С содержательной точки зрения употребление термина "устойчивость" в такой ситуации представляется вполне оправданным, поскольку рассматриваемая величина мало меняется при изменении объема выборки.
Рассмотрим проблему и методы оценки близости предельных распределений статистик и распределений, соответствующих конечным объемам выборок. При каких объемах выборок уже можно пользоваться предельными распределениями? Каков точный смысл термина "можно" в предыдущей фразе? Основное внимание уделяется переходу от точных формул допредельных распределений к пределу и применению метода статистических испытаний (Монте-Карло).
Начнем с обсуждения взаимоотношений асимптотической математической статистики и практики анализа статистических данных. Как обычно подходят к обработке реальных данных в конкретной задаче? Первым делом строят статистическую модель. Если хотят перенести выводы с совокупности результатов наблюдений на более широкую совокупность, например, предсказать чтолибо, то рассматривают, как правило, вероятностностатистическую модель. Например, традиционную модель выборки, в которой результаты наблюдений - реализации независимых (в совокупности) одинаково распределенных случайных величин. Очевидно, любая модель лишь приближенно соответствует реальности. В частности, естественно ожидать, что распределения результатов наблюдений несколько отличаются друг от друга, а сами результаты связаны между собой, хотя и слабо.
Итак, первый этап - переход от реальной ситуации к математической модели. Далее - неожиданность: на настоящем этапе своего развития математическая теория статистики зачастую не позволяет провести необходимые исследования для имеющихся объемов выборок. Более того, отдельные математики пытаются оправдать свой отрыв от практики соображениями о структуре этой теории, на первый взгляд убедительными. Неосторожная давняя фраза Б.В. Гнеденко и А.Н. Колмогорова: "Познавательная ценность теории вероятностей раскрывается только предельными теоремами" (см. классическую монографию [4], одну из наиболее ценных математических книг ХХ в.) взята на вооружение и более близкими к нам по времени авторами. Так, И.А. Ибрагимов и Р.З. Хасьминский пишут: "Решение неасимптотических задач оценивания, хотя и весьма важное само по себе, как правило, не может являться объектом достаточно общей математической теории. Более того, соответствующее решение часто зависит от конкретного типа распределения, объема выборки и т. д. Так, теория малых выборок из нормального закона будет отличаться от теории малых выборок из закона Пуассона" [6, с. 7].
Согласно цитированным и подобным им авторам, основное содержание математической теории статистики - предельные теоремы, полученные в предположении, что объемы рассматриваемых выборок стремятся к бесконечности. Эти теоремы опираются на предельные соотношения теории вероятностей типа Закона Больших Чисел и Центральной Предельной Теоремы. Подобные утверждения относятся к математике, т. е. к сфере чистой абстракции, и не могут быть непосредственно применены для анализа реальных данных. Их практическое использование, о котором "чистые" математики предпочитают не думать, опирается на важное предположение: "При данном объеме выборки достаточно точными являются асимптотические формулы".
Конечно, в качестве первого приближения представляется естественным воспользоваться асимптотическими формулами. Но это - лишь начало долгой цепи исследований. Как же обычно преодолевают разрыв между результатами асимптотической математической статистики и потребностями практики статистического анализа данных? Какие "подводные камни" подстерегают на этом пути?
Точные формулы и асимптотика. Начнем с наиболее продвинутой в математическом плане ситуации, когда для статистики известны как предельное распределение, так и распределения при конечных объемах выборки.
Примером является двухвыборочная односторонняя статистика Н.В. Смирнова.
Рассмотрим две независимые выборки объемов  и
и  из непрерывных функций распределения
из непрерывных функций распределения  и
и 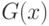 соответственно. Для проверки гипотезы однородности двух выборок
соответственно. Для проверки гипотезы однородности двух выборок 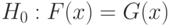 для всех действительных чисел
для всех действительных чисел  в 1939 г. Н.В. Смирнов в статье [22]
в 1939 г. Н.В. Смирнов в статье [22]
предложил использовать статистику

где 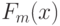 - эмпирическая функция распределения, построенная по первой выборке,
- эмпирическая функция распределения, построенная по первой выборке,  - эмпирическая функция распределения, построенная по второй выборке, супремум берется по всем действительным числам
- эмпирическая функция распределения, построенная по второй выборке, супремум берется по всем действительным числам  . Для обсуждения проблемы соотношения точных и предельных результатов ограничимся случаем равных объемов выборок, т. е.
. Для обсуждения проблемы соотношения точных и предельных результатов ограничимся случаем равных объемов выборок, т. е.  . Положим
. Положим

В цитированной статье [22] Н.В. Смирнов установил, что при безграничном возрастании объема выборки  вероятность
вероятность 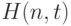 стремится к
стремится к 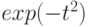 .
.
В работе [5] 1951 г. Б.В. Гнеденко и В.С. Королюк показали, что при целом 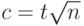 (именно при таких
(именно при таких  вероятность
вероятность 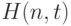 как функция
как функция  имеет скачки, поскольку статистика Смирнова
имеет скачки, поскольку статистика Смирнова 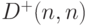 кратна
кратна 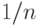 ) рассматриваемая вероятность
) рассматриваемая вероятность 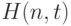 выражается через биномиальные коэффициенты, а именно,
выражается через биномиальные коэффициенты, а именно,
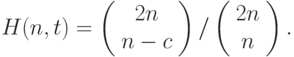 |
( 8.36) |
К сожалению, непосредственные расчеты по формуле (8.36) возможны лишь при сравнительно небольших объемах выборок, поскольку величина  ! (
! (  -факториал) уже при
-факториал) уже при 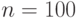 имеет более 200 цифр и не может быть без преобразований использована в вычислениях. Следовательно, наличие точной формулы для интересующей нас вероятности не снимает необходимости использования предельного распределения и изучения точности приближения с его помощью.
имеет более 200 цифр и не может быть без преобразований использована в вычислениях. Следовательно, наличие точной формулы для интересующей нас вероятности не снимает необходимости использования предельного распределения и изучения точности приближения с его помощью.
Широко известная формула Стирлинга для гаммафункции и, в частности, для факториалов позволяет преобразовать последнее выражение в асимптотическое разложение. То есть построить бесконечный степенной ряд (по степеням  ), такой, что каждая следующая частичная сумма дает все более точное приближение для интересующей нас вероятности
), такой, что каждая следующая частичная сумма дает все более точное приближение для интересующей нас вероятности  . Это сделано в работе А.А. Боровкова 1962 г. Большое количество подобных разложений для различных статистических задач приведено в работах В.М. Калинина и О.В. Шалаевского конца 1960-х - начала 1970-х гг. (Интересно отметить, что асимптотические разложения в ряде случаев расходятся, т.е. остаточные члены имеют нетривиальную природу.)
. Это сделано в работе А.А. Боровкова 1962 г. Большое количество подобных разложений для различных статистических задач приведено в работах В.М. Калинина и О.В. Шалаевского конца 1960-х - начала 1970-х гг. (Интересно отметить, что асимптотические разложения в ряде случаев расходятся, т.е. остаточные члены имеют нетривиальную природу.)
Затем в работах конца семидесятых годов сделана попытка теоретически оценить остаточный член второго порядка. Итоги подведены в монографии [16, §2.2, с.37-45]. Справедливо равенство
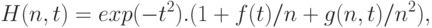
где
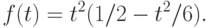
Целью последних из названных работ было получение равномерных по 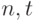 оценок остаточного члена второго порядка
оценок остаточного члена второго порядка 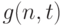 сверху и снизу в области, задаваемой условиями
сверху и снизу в области, задаваемой условиями
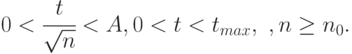 |
( 8.37) |
где  - некоторые параметры. С помощью длинных цепочек оценок остаточных членов в формулах, получаемых при преобразовании формулы (8.36) к предельному виду, сформулированная выше цель была достигнута. Для различных наборов параметров
- некоторые параметры. С помощью длинных цепочек оценок остаточных членов в формулах, получаемых при преобразовании формулы (8.36) к предельному виду, сформулированная выше цель была достигнута. Для различных наборов параметров  получены равномерные по
получены равномерные по  ,
,  оценки (сверху и снизу) остаточного члена второго порядка
оценки (сверху и снизу) остаточного члена второго порядка 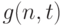 в области (8.37). Так, например,
в области (8.37). Так, например, 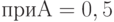 ,
,  ,
,  нижняя граница равна (
нижняя граница равна ( 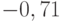 ), а верхняя есть
), а верхняя есть 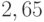 . Основные недостатки такого подхода:
. Основные недостатки такого подхода:
- зависимость оценок от параметров
 ,
,  ,
, 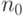 , задающих границы областей;
, задающих границы областей; - завышение оценок, иногда в сотни раз, обусловленное желанием получить равномерные оценки по области (оценкой реальной погрешности в конкретной точке является значение следующего члена асимптотического разложения).
Поэтому при составлении рассчитанной на практическое использование методики [15] проверки однородности двух выборок с помощью статистики Смирнова было решено перейти на несколько другую методологию (назовем ее "методологией заданной точности"), которую кратко можно описать следующим образом:
- выбирается достаточно малое положительное число
 , например
, например 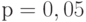 или
или 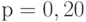 ;
; - приводятся точные значения
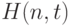 для всех значений
для всех значений  таких, что
таких, что 
- если же последнее неравенство не выполнено, то используется вместо
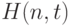 предельное значение
предельное значение 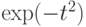 .
.
Принятая в методике [15] методология предполагает интенсивное использование вычислительной техники. Результатами расчетов являются граничные значения объемов выборок 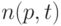 такие, что при меньших значениях объемов выборок рекомендуется пользоваться точными значениями функции распределения статистики Смирнова, а при больших - предельными. Описывается этот результат таблицей, а не формулой. При построении реальных таблиц не обойтись без выбора того или иного конкретного значения
такие, что при меньших значениях объемов выборок рекомендуется пользоваться точными значениями функции распределения статистики Смирнова, а при больших - предельными. Описывается этот результат таблицей, а не формулой. При построении реальных таблиц не обойтись без выбора того или иного конкретного значения  , задающего объемы таблиц.
, задающего объемы таблиц.
Оценки скорости сходимости. Теоретические оценки скорости сходимости в различных задачах прикладной математической статистики иногда формулируются в весьма абстрактном виде. Так, в 1960-1970-х гг. была популярна задача оценки скорости сходимости распределения классической статистики омегаквадрат (Крамера-Мизеса-Смирнова).
Для максимума модуля разности допредельной и предельной функций распределения
этой статистики различные авторы доказывали, что для любого  существует константа
существует константа  , такая, что он не превосходит
, такая, что он не превосходит 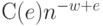 . Прогресс состоял в увеличении константы
. Прогресс состоял в увеличении константы  . Сформулированный выше результат был доказан последовательно для
. Сформулированный выше результат был доказан последовательно для 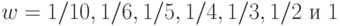 [16].
[16].
Конечно, все эти исследования не могли дать конкретных практических рекомендаций. Однако необходимой исходной точкой является само существование предельного распределения. Представим себе, что некто, не зная, что у распределения Коши нет математического ожидания, моделирует выборочные средние арифметические результатов наблюдений из этого распределения. Ясно, что его попытки оценить скорость сходимости выборочных средних к пределу обречены на провал.
Последовательное улучшение теоретических оценок скорости сходимости дает надежду на быструю реальную сходимость. Действительно, численные расчеты показали, что предельным распределением для статистики омегаквадрат (Крамера-Мизеса-Смирнова) можно пользоваться уже при объеме выборки, равном 4.
Использование датчиков псевдослучайных чисел. Если же предельное распределение известно, то возникает возможность изучить скорость сходимости численно методом статистических испытаний (Монте-Карло). Однако при этом обычно возникают две проблемы.
Во-первых, откуда известно, что скорость сходимости монотонна? Если при данном объеме выборки различие мало, то будет ли оно мало и при дальнейших объемах? Иногда отклонения допредельного распределения от предельного объясняются довольно сложными причинами. Так, для распределения хиквадрат они связаны с рядом до сих пор не решенных теоретикочисловых проблем о числе целых точек в эллипсоиде растущего диаметра.
Во-вторых, с помощью датчиков псевдослучайных чисел получаем допредельные распределения с погрешностью, которая может преуменьшать различие. Поясним мысль аналогией. Растущий сигнал измеряется с погрешностями. Когда можно гарантировать, что его величина наверняка превзошла заданную границу?
Напомним, что проблема качества датчиков псевдослучайных чисел продолжает оставаться открытой (см. главу 11 в [18]). Для моделирования в пространствах фиксированной размерности датчики псевдослучайных чисел решают поставленные задачи. Но для рассматриваемых здесь задач размерность не фиксирована - мы не знаем, при каком конкретно объеме выборки можно переходить к предельному распределению согласно "методологии заданной точности".
Нужны дальнейшие работы по изучению качества датчиков псевдослучайных чисел в задачах неопределенной размерности. Поскольку критиков датчиков обычно обвиняют в том, что они сами их не используют, отметим, что мы применяли этот инструментарий при изучении помех, создаваемых электровозами (см. монографию [16]), при изучении статистических критериев проверки однородности двух выборок (см. работу [9]).
А нужна ли вообще асимптотика? В настоящее время развивается актуальное направление прикладной статистики, связанное с интенсивным использованием вычислительной техники для изучения свойств статистических процедур. Как уже отмечалось, математические методы в статистике обычно позволяют получать лишь асимптотические результаты, и для переноса выводов на конечные объемы выборок приходится применять вычислительные методы. Например, в Новосибирском государственном техническом университете разработан и активно применяется подход, основанный на интенсивном использовании современной вычислительной техники. Основная идея такова: в качестве альтернативы асимптотическим методам математической статистики используется анализ результатов статистического моделирования (порядка 2000 испытаний) выборок конкретных объемов (200, 500, 1000). При этом анализ предельных распределений заменяется на анализ распределений соответствующих статистик при указанных объемах выборок.
К достоинствам этого подхода относится возможность замены теоретических исследований расчетами. Разработанная программная система дает (в принципе) возможность численно изучить свойства любого статистического алгоритма для любого конкретного распределения результатов наблюдений и любого конкретного объема выборки. Недостатки рассматриваемого подхода: зависимость от свойств датчиков псевдослучайных чисел; неизвестность предельного распределения (и даже самого факта его существования), а потому невозможность обоснованного переноса полученных выводов на объемы выборок, отличные от исследованных. Поэтому с точки зрения теории математической статистики полученные рассматриваемым способом результаты следует рассматривать как правдоподобные (а не доказательные, как в классической математической статистике).
Кроме того, они принципиально неточные. Даже в наиболее благоприятных условиях отклонение (в метрике "супремум разности") смоделированного распределения, построенного по 2000 испытаниям, от теоретического предельного распределения может достигать 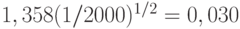 . Это означает, что процентные точки, соответствующие уровням значимости 0,05 и особенно 0,01, могут сильно отличаться от соответствующих процентных точек предельных распределений. Очевидно, следующий этап работ - изучение точности полученных в рассматриваемом подходе выводов, прежде всего приближений и процентных точек.
. Это означает, что процентные точки, соответствующие уровням значимости 0,05 и особенно 0,01, могут сильно отличаться от соответствующих процентных точек предельных распределений. Очевидно, следующий этап работ - изучение точности полученных в рассматриваемом подходе выводов, прежде всего приближений и процентных точек.
Весьма полезными и интересными являются результаты, касающиеся непараметрических критериев согласия и построения оптимального группирования, в частности, при использовании критериев типа хиквадрат.
В работе [11] сравниваются два плана контроля надежности технических изделий. Оказывается, что при объемах выборки, меньших 150, лучше первый план, а при объемах, больших 150 - второй. Значит, если бы по новосибирскому методу сравнивались эти планы при достаточно большом объеме выборки  , то лучшим был бы признан первый план, что неверно - наступит момент (объем выборки), когда лучшим станет второй план.
, то лучшим был бы признан первый план, что неверно - наступит момент (объем выборки), когда лучшим станет второй план.
Другая относящаяся к делу ассоциация - из весьма содержательной монографии о прикладной математике [2]. Будем суммировать бесконечный ряд с членами 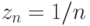 . Поскольку члены его убывают, то обычно используемые алгоритмы остановят вычисления на какомто шагу. А сумма-то - бесконечна!
. Поскольку члены его убывают, то обычно используемые алгоритмы остановят вычисления на какомто шагу. А сумма-то - бесконечна!
Кажется, что компьютер дал универсальную отмычку ко всем проблемам вообще и в области прикладной статистики в частности. Но это только кажется.
Принцип уравнивания погрешностей: погрешности различной природы должны вносить примерно одинаковый вклад в общую погрешность математической модели. Так, определение рационального объема выборки в статистике интервальных данных основано на уравнивании влияния метрологической и статистической погрешностей. Согласно подходу [16], выбор числа градаций в социологических анкетах целесообразно проводить на основе уравнивания погрешностей квантования и неопределенности в ответах респондентов. В классической модели управления запасами целесообразно уравнять влияние неточностей в определении параметров на отклонение целевой функции от оптимума. Из принципа уравнивания погрешностей следует, что относительные погрешности определения параметров модели должны совпадать. Погрешность, порожденная отклонением спроса от линейного, оценивается по данным об отпуске товаров. Это дает возможность оценить допустимые отклонения для других параметров. В частности, установить, что ра схождения между методиками не являются существенными [16].
В терминах общей схемы устойчивости рассмотрим для простоты записи случай двух параметров. Пусть 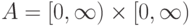 и
и 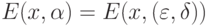 , где
, где 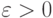 и
и 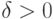 задают точность определения соответствующих параметров, так что
задают точность определения соответствующих параметров, так что  при
при  ,
,  . Пусть \varepsilon задано, а \delta исследователь может выбрать, причем известно, что уменьшение \delta связано с увеличением расходов. Как выбирать
. Пусть \varepsilon задано, а \delta исследователь может выбрать, причем известно, что уменьшение \delta связано с увеличением расходов. Как выбирать 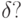 Представляется естественным "уравнять" отклонения, порожденные различными параметрами, т. е. определить
Представляется естественным "уравнять" отклонения, порожденные различными параметрами, т. е. определить  из условия
из условия
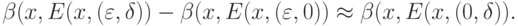 |
( 8.38) |
Если затраты и полезный эффект точно известны, то \delta можно определить путем решения соответствующей оптимизационной задачи. В противном случае соотношение (8.38) предлагается использовать в качестве эвристического правила.

