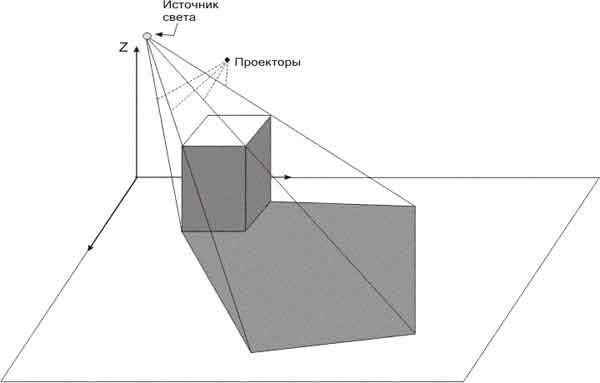
| Отрезок пересекает левую и нижнюю границу клиппирующего окна.Чему могут быть равны коды его концов по алгоритму Сазерленда - Коэ |
Визуализация пространственных реалистических сцен
Свето-теневой анализ
Тени возникают как результат экранирования источника света предметами, составляющими сцену. При этом существуют полные тени и полутени, что связано с физической природой света: полная тень образуется в центральной части затенения, а полутень - вблизи ее границ. В нашем курсе мы будем касаться только полной тени, хотя и существуют технологии изображения полутеней, сопровождающиеся большим объемом вычислений.
Если считать, что наблюдатель находится в одной точке с источником света, то тени в наблюдаемой сцене не возникают: затеняемая область является невидимой. Во всех прочих случаях тени видны. Источник света может находиться на бесконечности или на конечном расстоянии, причем во втором случае он может оказаться в поле зрения наблюдателя.
Для бесконечно удаленного источника света тени на картинной плоскости получаются в результате параллельной проекции объектов, а для близкого источника - центральной проекции. Объекты и их части становятся невидимыми, если они попадают в область тени, поэтому при построении изображения задача об удалении невидимых областей решается дважды: относительно наблюдателя в процессе проецирования и относительно источника света. При определении расположения теней строятся проекции невидимых с позиции источника света граней (неосвещенных) на картинную плоскость, в результате чего получаются теневые многоугольники. Эти многоугольники строятся для всех объектов сцены и заносятся в список. Отметим, что теневые многоугольники не зависят от положения наблюдателя, поэтому при осмотре сцен с различных точек зрения они строятся только один раз. Неосвещенные области определяются теми же методами, которые были описаны ранее в "Проецирование пространственных сцен" , а для построения проекций используются методы, некоторые из которых описаны в "Растровое преобразование графических примитивов" . В частности, можно применять матрицы проекций в однородной системе координат.
Впервые идея совмещенного анализа видимости и затененности была предложена в 1968 г. Аппелем. В качестве примера рассмотрим один алгоритм на основе построчного сканирования, состоящий из двух основных этапов.
I. Анализ сцены по отношению к источнику света. Для всех
многоугольников, полученных в результате проецирования сцены,
определяются неосвещенные (затененные) участки и теневые
многоугольники (проекционные тени), причем многоугольники образуют
пронумерованный список. Для этих многоугольников формируется матрица 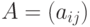 , позволяющая определить, отбрасывает ли многоугольник тень и какие из
многоугольников он может закрывать. Если для некоторых значений
, позволяющая определить, отбрасывает ли многоугольник тень и какие из
многоугольников он может закрывать. Если для некоторых значений 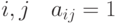 ,
то это означает, что многоугольник с номером
,
то это означает, что многоугольник с номером  может отбрасывать тень
на многоугольник с номером
может отбрасывать тень
на многоугольник с номером  .
.
Таким образом, на этом этапе основным является вопрос об
эффективном алгоритме построения такой матрицы. Если проекция включает  многоугольников, то необходимо рассмотреть "взаимоотношения"
многоугольников, то необходимо рассмотреть "взаимоотношения" 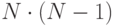 пар
многоугольников. Сократить перебор можно за счет погружения объектов в
прямоугольные или сферические оболочки или путем использования
сортировки по глубине.
пар
многоугольников. Сократить перебор можно за счет погружения объектов в
прямоугольные или сферические оболочки или путем использования
сортировки по глубине.
II. Анализ сцены по отношению к наблюдателю. Выполняются два процесса сканирования. Первый - для определения отрезков, видимых с позиции наблюдателя (о нем рассказывалось раньше в "Проецирование пространственных сцен" ). Второй - для определения пересечений отрезков с теневыми многоугольниками из списка. Рекурсивный алгоритм второго сканирования состоит из четырех основных шагов.
Для каждого видимого отрезка
- Если нет ни одного теневого многоугольника, то отрезок изображается с основной интенсивностью.
- Если многоугольник, содержащий видимый отрезок, не пересекается с теневыми многоугольниками, то отрезок изображается с основной интенсивностью.
- Если отрезок полностью закрывается некоторыми теневыми многоугольниками, то интенсивность его изображения определяется с учетом затенения всеми этими многоугольниками.
- Если несколько теневых многоугольников частично закрывают отрезок, то он разбивается на ряд отрезков точками пересечения с теневыми многоугольниками.
Этот алгоритм предполагает, что затенение не абсолютное, т.е. затененные участки все-таки являются видимыми, только их освещенность падает в зависимости от количества и освещенности затеняющих многоугольников. При полном затенении в третьем пункте алгоритма отрезок становится полностью невидимым, а в четвертом дальнейшему анализу подвергаются только незатененные отрезки.
Способы расчета интенсивности при неполном затенении могут быть различны. В этом случае все затененные многоугольники имеют свою интенсивность в зависимости от выбранной модели освещенности. При этом можно учитывать расстояние затененного участка от поверхности, отбрасывающей тень.
Еще один алгоритм, часто применяемый при построении теней, носит название метода теневого буфера. Он строится на основе метода Z-буфера, описанного в "Проецирование пространственных сцен" . Теневой буфер - это тот же Z-буфер, только с точки зрения источника света. Таким образом, используются два буфера: один - для расстояния от картинной плоскости до точек изображаемой сцены, а другой - для расстояний от этих же точек до источника света. Алгоритм позволяет изображать сцены с полным затенением и сводится к двум основным этапам:
- Cцена рассматривается из точки расположения источника света в соответствующей системе координат. Итогом построения является полностью заполненный теневой буфер.
- Сцена рассматривается с точки зрения наблюдателя, применяется обычный метод Z-буфера с небольшим дополнением. Если точка
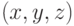 является видимой в этой системе координат, то вычисляются ее координаты в системе, связанной с источником света -
является видимой в этой системе координат, то вычисляются ее координаты в системе, связанной с источником света - 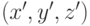 , затем проверяется, является ли точка видимой с этой позиции. Для этого значение
, затем проверяется, является ли точка видимой с этой позиции. Для этого значение 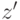 сравнивается со значением, содержащимся в теневом буфере для этой точки, и в случае видимости значение интенсивности заносится в буфер кадра в точке
сравнивается со значением, содержащимся в теневом буфере для этой точки, и в случае видимости значение интенсивности заносится в буфер кадра в точке  .
.
Оба приведенных алгоритма работают в пространстве изображения, т. е. имеют дело с проекциями на плоскость и некоторой дополнительной информацией о точках сцены, соответствующих этим проекциям. Существуют алгоритмы, работающие в трехмерном объектном пространстве. В частности, для построения теней используются модификации алгоритма Вейлера-Азертона, описанного в "Проецирование пространственных сцен" . Модификация заключается в том, что, как и в случае теневого буфера, задача удаления невидимых граней решается сначала с позиции источника света, а затем полученная информация об объектах используется при построении изображения с позиции наблюдателя. В общих чертах шаги алгоритма можно описать так:
- Определяются грани, видимые из точки расположения источника света. С целью повышения эффективности запоминается информация только о видимых гранях. Поскольку анализ выполняется в системе координат, связанной с источником света, то полученные видимые многоугольники затем заново приводятся к исходной системе координат. Многоугольники связываются с гранями, которым они принадлежат (в результате затенения одна грань может содержать несколько многоугольников).
- Сцена обрабатывается из положения наблюдателя. При изображении видимой грани учитываются только те многоугольники, которые входят в список, полученный на первом этапе, т.е. грань рассматривается как совокупность таких многоугольников.
При наличии нескольких источников света количество освещенных участков естественным образом увеличивается.