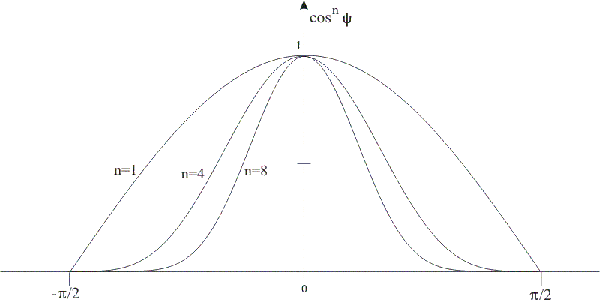
| Отрезок пересекает левую и нижнюю границу клиппирующего окна.Чему могут быть равны коды его концов по алгоритму Сазерленда - Коэ |
Закрашивание. Рендеринг полигональных моделей
Визуальное восприятие объектов окружающей действительности представляет собой сложный процесс, имеющий как физические, так и психологические аспекты. Во второй главе мы уже обсуждали некоторые особенности восприятия света и цвета глазом человека. К тому, что уже было сказано о спектральной чувствительности глаза, надо добавить еще несколько моментов.
Глаз адаптируется к средней яркости рассматриваемой сцены, поэтому при смене фона изменяется восприятие сцены. Например, однородно окрашенная область на более темном фоне будет казаться более яркой, чем на светлом. Кроме того, она будет восприниматься как более обширная (рис. 9.1).
Еще одна особенность восприятия заключается в том, что граница равномерно освещенной области кажется более яркой по сравнению с внутренними частями. Это явление было обнаружено Эрнстом Махом, поэтому оно получило название эффекта полос Маха. Такие особенности необходимо учитывать, если мы стремимся к созданию реалистических изображений сцен.
При формировании изображения сцен, содержащих зеркальные и полупрозрачные поверхности, следует использовать законы геометрической оптики, преломляющие свойства материалов, эффекты смешения цветов и т.д.
Простая модель освещения
Объекты окружающего пространства становятся видимыми для глаза благодаря световой энергии, которая может излучаться поверхностью предмета, отражаться или проходить сквозь нее. В свою очередь, отражение света от поверхности зависит от физических свойств материала, из которого она изготовлена, а также от характера и расположения источника света. Яркость (или интенсивность) освещения зависит от энергии светового потока, которая обуславливается, во- первых, мощностью источника света, а во-вторых, отражающими и пропускающими свойствами объекта.
Сначала мы рассмотрим модель освещения, учитывающую только отражение. Свойства отраженного света зависят главным образом от направления лучей и характеристик отражающей поверхности.
Отражение может быть двух видов: диффузное и зеркальное. Первое из них возникает в ситуации, когда свет как бы проникает под поверхность объекта, поглощается, а потом равномерно излучается во всех направлениях. Поверхность в этом случае рассматривается как идеальный рассеиватель. При этом возникает эффект матового света, а видимая освещенность того или иного участка поверхности не зависит от положения наблюдателя. Зеркальное отражение, наоборот, происходит от внешней поверхности, интенсивность его неоднородна, поэтому видимый максимум освещенности зависит от положения глаза наблюдателя.
Свет точечного источника отражается от поверхности рассеивателя по
закону Ламберта: интенсивность отражения пропорциональна косинусу угла
между внешней нормалью к поверхности и направлением к источнику света
(рис. 9.2). Если 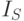 - интенсивность источника света,
- интенсивность источника света,  - угол между
вектором внешней нормали к поверхности и направлением к источнику
света, то интенсивность отраженного света определяется формулой
- угол между
вектором внешней нормали к поверхности и направлением к источнику
света, то интенсивность отраженного света определяется формулой
 |
( 9.1) |
При таком расчете интенсивности получится очень контрастная
картина, т.к. участки поверхности, на которые лучи от источника не
попадают напрямую, останутся абсолютно черными. Для повышения
реалистичности необходимо учитывать рассеивание света в окружающем
пространстве. Поэтому вводится фоновая освещенность, зависящая от
интенсивности рассеянного света  , и интенсивность отраженного света
определяется выражением
, и интенсивность отраженного света
определяется выражением
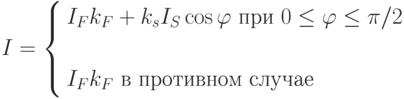 |
( 9.2) |
 - коэффициент диффузного отражения рассеянного света,
- коэффициент диффузного отражения рассеянного света, 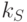 -
коэффициент диффузного отражения падающего света,
-
коэффициент диффузного отражения падающего света, 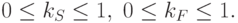
В описанной модели пока никак не учитывалась удаленность источника света от поверхности, поэтому по освещенности двух объектов нельзя судить об их взаимном расположении в пространстве. Если мы хотим получить перспективное изображение, то необходимо включить затухание интенсивности с расстоянием. Обычно интенсивность света обратно пропорциональна квадрату расстояния от источника. В качестве расстояния до источника в случае перспективного преобразования можно взять расстояние до центра проекции, и если он достаточно удален, то изображение будет достаточно адекватным. Но если этот центр расположен близко к объекту, то квадрат расстояния меняется очень быстро, и в этом случае лучше использовать линейное затухание. В этом случае интенсивность отраженного света от непосредственно освещенных участков поверхности будет задаваться формулой
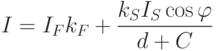 |
( 9.3) |
 - расстояние до центра проекции, а
- расстояние до центра проекции, а  - произвольная постоянная.
Если центр проекции находится на бесконечности, т. е. при параллельном
проецировании, то в качестве
- произвольная постоянная.
Если центр проекции находится на бесконечности, т. е. при параллельном
проецировании, то в качестве  можно взять расстояние до объекта,
наиболее близкого к наблюдателю.
можно взять расстояние до объекта,
наиболее близкого к наблюдателю.В отличие от диффузного, зеркальное отражение является направленным. Идеальное зеркало отражает лучи по принципу "отраженный и падающий лучи лежат в одной плоскости, причем угол падения равен углу отражения" (имеется в виду угол между направлением луча и нормалью к поверхности). Если поверхность не идеально зеркальная, то лучи отражаются в различных направлениях, но с разной интенсивностью, а функция изменения интенсивности имеет четко выраженный максимум. Поскольку физические свойства зеркального отражения довольно сложны, то в компьютерной графике используется эмпирическая модель Фонга. Суть ее заключается в том, что для глаза наблюдателя интенсивность зеркально отраженного луча зависит от угла между идеально отраженным лучом и направлением к наблюдателю (рис. 9.3a). Кроме того, поскольку зеркальное отражение зависит еще и от длины волны, это также будем учитывать в формуле для вычисления интенсивности. Модель Фонга описывается соотношением
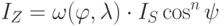 |
( 9.4) |
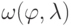 - функция отражения,
- функция отражения,  - длина волны. Степень, в которую
возводится косинус угла, влияет на размеры светового блика,
наблюдаемого зрителем. Графики этой функции приведены на рис. 9.4, и
они как раз являются характерными кривыми поведения функции изменения
интенсивности в зависимости от свойств поверхности.
- длина волны. Степень, в которую
возводится косинус угла, влияет на размеры светового блика,
наблюдаемого зрителем. Графики этой функции приведены на рис. 9.4, и
они как раз являются характерными кривыми поведения функции изменения
интенсивности в зависимости от свойств поверхности.Теперь модель освещенности, учитывающую зеркальное и диффузное отражения, можно описать формулой
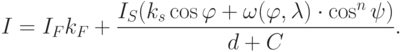 |
( 9.5) |
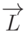 (направление к источнику) и
(направление к источнику) и  (внешняя
нормаль), косинус угла
(внешняя
нормаль), косинус угла  можно вычислить через скалярное произведение:
можно вычислить через скалярное произведение: 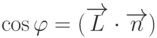 . Для расчета интенсивности зеркального отражения сначала надо
определить отраженный вектор
. Для расчета интенсивности зеркального отражения сначала надо
определить отраженный вектор 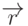 . Из рис. 9.3b видно, что
. Из рис. 9.3b видно, что 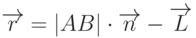 . С другой
стороны
. С другой
стороны 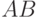 является диагональю ромба
является диагональю ромба 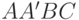 , поэтому
, поэтому 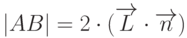 . Учитывая все эти
соотношения, получаем формулу
. Учитывая все эти
соотношения, получаем формулу![I=I_Fk_F+\frac{I_S\{k_s(\overrightarrow{L}\cdot\overrightarrow{n})+\omega(\varphi,\lambda)\cdot[2\cdot(\overrightarrow{L}\cdot\overrightarrow{n})\cdot(\overrightarrow{e}\cdot\overrightarrow{n})-(\overrightarrow{e}\cdot\overrightarrow{L})]^n\}}{d+C}.](/sites/default/files/tex_cache/6061e6ff5194adec8d0cd32018ee34d2.png) |
( 9.6) |
В алгоритмах закрашивания с использованием цветовых моделей интенсивность рассчитывается для каждого из базовых цветов, поскольку изменение интенсивности при зеркальном отражении зависит от длины волны.