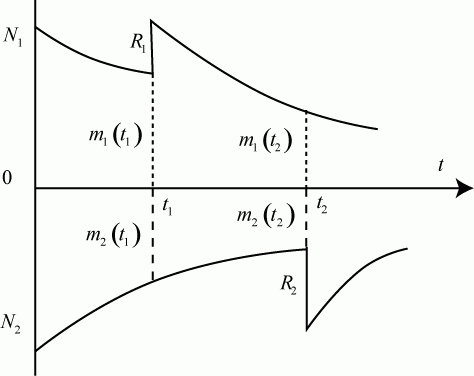| Высшее образование |
Типовые математические модели
2.8.2. Высокоорганизованный бой с пополнением группировок
В ходе боя противоборствующие стороны могут вводить резервы. Пусть сторона А вводит резерв 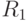 в момент времени
в момент времени 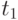 , сторона Б - резерв
, сторона Б - резерв 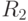 в момент времени
в момент времени 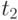 . Такую ситуацию можно наглядно представить диаграммой (рис. 2.23).
. Такую ситуацию можно наглядно представить диаграммой (рис. 2.23).
Весь интервал исследования содержит три подинтервала, так в сумме резервы обеими сторонами вводятся три раза.
-
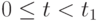 . Значения
. Значения  и
и 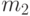 находятся интегрированием уравнения динамики боя (2.3) при начальных условиях
находятся интегрированием уравнения динамики боя (2.3) при начальных условиях  и
и 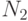 .
. -
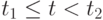 . Значения
. Значения  и
и 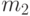 на этом временном участке находятся интегрированием тех же уравнений динамики боя (2.3), но при начальных условиях
на этом временном участке находятся интегрированием тех же уравнений динамики боя (2.3), но при начальных условиях  и
и 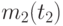 .
. -
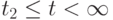 . Значения
. Значения  и
и 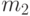 на этом временном участке находятся интегрированием тех же уравнений динамики боя (2.3), но при начальных условиях
на этом временном участке находятся интегрированием тех же уравнений динамики боя (2.3), но при начальных условиях  и
и 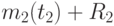 .
.
2.8.3. Высокоорганизованный бой с упреждением ударов
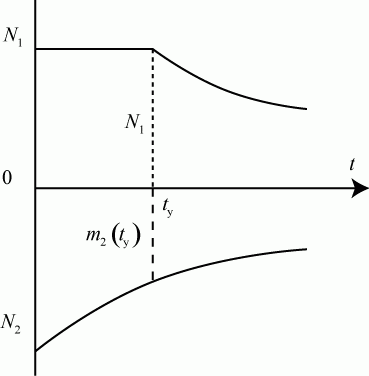
Предположим, что одна из сторон, например, сторона А, ведет огонь в то время, когда сторона Б еще не в состоянии ответить. Представим эту ситуацию диаграммой (рис. 2.24).
Цель моделирования также состоит в определении  и
и 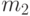 на любой момент противоборства сторон. Как и в предыдущем случае, решение находится по частям для каждого характерного временного промежутка. Здесь их два.
на любой момент противоборства сторон. Как и в предыдущем случае, решение находится по частям для каждого характерного временного промежутка. Здесь их два.
-
 . На этом временном промежутке огонь ведет только сторона А (
. На этом временном промежутке огонь ведет только сторона А (  - время упреждения). Уравнения динамики боя здесь выглядят так:
- время упреждения). Уравнения динамики боя здесь выглядят так:

Значения
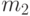 находят интегрированием при начальном условии
находят интегрированием при начальном условии  .
. -
 . Значения
. Значения  и
и 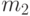 на этом участке также находятся интегрированием уравнений динамики средних, но при начальных условиях
на этом участке также находятся интегрированием уравнений динамики средних, но при начальных условиях  и
и  . Величина
. Величина  известна, а величину
известна, а величину 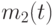 найдем из уравнения
найдем из уравнения 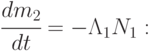

2.8.4. Модель боя с неполной информацией
Боевые единицы двух противоборствующих сторон распределены случайно (для противоположной стороны) на площадях  и
и 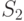 . Каждая боевая единица занимает некоторую площадь - позицию, величина которой
. Каждая боевая единица занимает некоторую площадь - позицию, величина которой 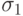 и
и 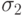 у сторон А и Б соответственно. Цель уничтожается при попадании заряда в площадь цели.
у сторон А и Б соответственно. Цель уничтожается при попадании заряда в площадь цели.
Схематично такое противоборство показано на рис. 2.25.
Как и в предыдущих случаях,  и
и 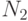 - первоначальные численности боевых единиц, скорострельности боевых единиц
- первоначальные численности боевых единиц, скорострельности боевых единиц 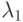 и
и  , вероятности поражения одним выстрелом -
, вероятности поражения одним выстрелом - 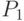 и
и  сторон А и Б соответственно.
сторон А и Б соответственно.
Огонь по площадям  и
и 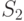 ведется неприцельно.
ведется неприцельно.
Цель моделирования - определение среднего числа непораженных целей  и
и 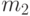 на каждый момент времени ведения огня.
на каждый момент времени ведения огня.
Уравнения динамики боя соответствуют уравнениям динамики средних (2.3). Однако, в отличие от высокоорганизованного боя, вероятности 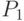 и
и  зависят от числа непораженных целей
зависят от числа непораженных целей  и
и 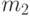 :
:

Следовательно, уравнения имеют вид:

Начальные условия для интегрирования:  и
и  .
.
Если площади целей различны (  ), то в уравнениях очевидны замены:
), то в уравнениях очевидны замены:
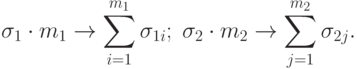
2.8.5. Учет запаздывания в переносе и открытии огня
Такая ситуация возможна при плохой разведке, связи, управлении огнем.
Пусть  - время запаздывания открытия огня стороной А,
- время запаздывания открытия огня стороной А, 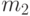 - стороной Б. Тогда интенсивности потоков поражающих выстрелов сторон, приходящихся на одну цель, равны:
- стороной Б. Тогда интенсивности потоков поражающих выстрелов сторон, приходящихся на одну цель, равны:
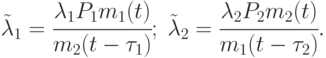
Уравнения динамики боя принимают вид:
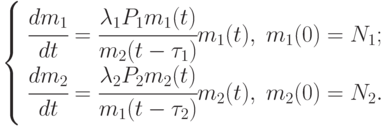
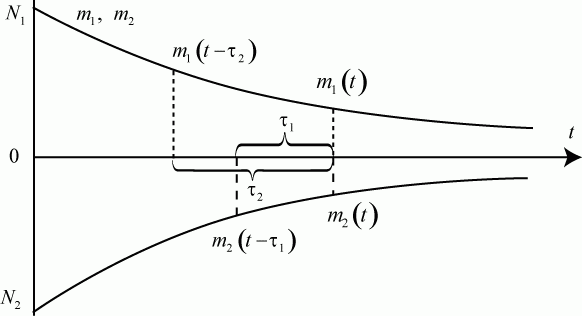
На рис. 2.26 в момент времени  действительные значения боеспособных средств сторон равны
действительные значения боеспособных средств сторон равны 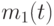 и
и 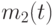 . Но в это время сторона А ведет огонь по целям, разведанным ранее, в момент времени
. Но в это время сторона А ведет огонь по целям, разведанным ранее, в момент времени 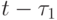 ; сторона Б - по целям, разведанным в момент времени
; сторона Б - по целям, разведанным в момент времени 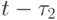 .
.
Ценность рассмотренных моделей противоборства сторон в функциональном плане всегда ограничена - об этом было сказано в начале п. 2.8. Но они, бесспорно, расширяют наши представления о приемах и подходах к аналитическому моделированию сложных процессов.
Вопросы для самоконтроля
- Что такое аналитическая модель? Ее отличия от других моделей.
- Определение марковского случайного процесса. Причина "популярности" моделирования по схеме марковских процессов.
- Что такое однородный и неоднородный марковские процессы?
- Правило составления уравнений Колмогорова.
- Эргодическая теорема Маркова.
- Схема "гибели и размножения".
- Характеристика элементов СМО.
- Показатели СМО с отказами.
- Показатели СМО с ожиданием.
- Одноканальная СМО с очередью на 4 заявки и конечной надежностью канала. В момент отказа заявка, которая обслуживалась в канале, возвращается в очередь, если там есть место, иначе теряется. Во время ремонта заявки в СМО не поступают. Интенсивности поступления и обслуживания заявок
 и
и  , соответственно. Интенсивности выхода из строя и ремонта канала
, соответственно. Интенсивности выхода из строя и ремонта канала  и
и  соответственно. Описать состояния системы, составить размеченный граф состояний, уравнения Колмогорова и систему алгебраических уравнений для вычисления предельных вероятностей состояний системы. Привести пример количественного решения полученных уравнений в математической программе.
соответственно. Описать состояния системы, составить размеченный граф состояний, уравнения Колмогорова и систему алгебраических уравнений для вычисления предельных вероятностей состояний системы. Привести пример количественного решения полученных уравнений в математической программе. - Двухканальная СМО с очередью на 4 заявки и конечной надежностью канала. В момент отказа заявки, которые обслуживались в канале, возвращаются в очередь, если там есть место, иначе теряются. Во время ремонта заявки в СМО не поступают. Интенсивности поступления и обслуживания заявок
 и
и  , соответственно. Интенсивности выхода из строя и ремонта канала
, соответственно. Интенсивности выхода из строя и ремонта канала  и
и  соответственно. Описать состояния системы, составить размеченный граф состояний, уравнения Колмогорова и систему алгебраических уравнений для вычисления предельных вероятностей состояний системы. Привести пример количественного решения полученных уравнений в математической программе.
соответственно. Описать состояния системы, составить размеченный граф состояний, уравнения Колмогорова и систему алгебраических уравнений для вычисления предельных вероятностей состояний системы. Привести пример количественного решения полученных уравнений в математической программе. - Зачем нужно знать метод динамики средних?
- Допущения при выводе моделей динамики средних.
- В организации 2000 однотипных приборов, каждый из которых может быть в одном из трех состояний: исправен, находиться в ремонте в мастерской организации (МО), на ремонтном предприятии. Интенсивность выхода из строя
 . В МО прибор может быть отремонтирован и возвращен в организацию, либо отправлен на ремонтное предприятие. Средняя длительность ремонта в МО
. В МО прибор может быть отремонтирован и возвращен в организацию, либо отправлен на ремонтное предприятие. Средняя длительность ремонта в МО  , а интенсивность отправки на предприятие
, а интенсивность отправки на предприятие  . Средняя длительность ремонта на предприятии
. Средняя длительность ремонта на предприятии  . После ремонта на предприятии прибор возвращается в организацию. Составить аналитическую модель с целью определения средних численностей приборов в каждом состоянии. Привести пример количественного решения полученных уравнений в математической программе.
. После ремонта на предприятии прибор возвращается в организацию. Составить аналитическую модель с целью определения средних численностей приборов в каждом состоянии. Привести пример количественного решения полученных уравнений в математической программе. - Сформулируйте принцип квазирегулярности. Когда возникает необходимость его применения?
- Применение метода динамики средних при выводе модели противоборства двух сторон.
- Как учесть в модели противоборства ввод резервов?
- Как учесть в модели противоборства упреждающие удары одной из сторон?
- Как учесть в модели противоборства отсутствие разведки в ходе обмена ударами?
- Как учесть в модели противоборства запаздывание в переносе огня?