| Высшее образование |
Типовые математические модели
2.2. Моделирование по схеме непрерывных марковских процессов
Существует широкий класс систем, которые меняют свои состояния в случайные моменты времени  . Как и в предыдущем случае, в этих системах рассматривается процесс с дискретными состояниями
. Как и в предыдущем случае, в этих системах рассматривается процесс с дискретными состояниями  . Например, переход объекта от исправного состояния к неисправному, соотношение сил сторон в ходе боя и т. п. Оценка эффективности таких систем определяется с помощью вероятностей каждого состояния
. Например, переход объекта от исправного состояния к неисправному, соотношение сил сторон в ходе боя и т. п. Оценка эффективности таких систем определяется с помощью вероятностей каждого состояния 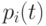 на любой момент времени
на любой момент времени  ,
, 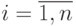 .
.
Чтобы определить вероятности состояния системы 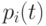 для любого момента времени
для любого момента времени  необходимо воспользоваться математическими моделями марковских процессов с непрерывным временем (непрерывных марковских процессов).
необходимо воспользоваться математическими моделями марковских процессов с непрерывным временем (непрерывных марковских процессов).
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 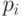 , так как вероятность "перескока" системы из одного состояния в другое точно в момент времени
, так как вероятность "перескока" системы из одного состояния в другое точно в момент времени  равна нулю (как вероятность любого отдельного значения непрерывной случайной величины).
равна нулю (как вероятность любого отдельного значения непрерывной случайной величины).
Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 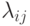 :
:

где 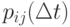 - вероятность того, что система, находившаяся в момент времени
- вероятность того, что система, находившаяся в момент времени  в состоянии
в состоянии  за время
за время  перейдет в состояние
перейдет в состояние 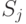 .
.
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
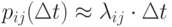
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 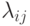 не зависят от времени
не зависят от времени  (от момента начала промежутка
(от момента начала промежутка  ). В противном случае непрерывный марковский процесс называется неоднородным.
). В противном случае непрерывный марковский процесс называется неоднородным.
Целью моделирования, как и в случае дискретных процессов, является определение вероятностей состояний системы 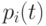 . Эти вероятности находятся интегрированием системы дифференциальных уравнений Колмогорова.
. Эти вероятности находятся интегрированием системы дифференциальных уравнений Колмогорова.
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
- Определить состояния системы и плотности вероятностей переходов
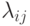 .
. - Составить и разметить граф состояний.
- Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
- B левой части уравнения записывается производная вероятности
 -го состоянии
-го состоянии 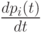 .
. - В правой части записывается алгебраическая сумма произведений
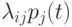 и
и  . Число произведений столько, сколько стрелок связано с данным состоянием. Если стрелка графа направлена в данное состояние, то соответствующее произведение имеет знак плюс, если из данного состояния - минус.
. Число произведений столько, сколько стрелок связано с данным состоянием. Если стрелка графа направлена в данное состояние, то соответствующее произведение имеет знак плюс, если из данного состояния - минус. - Определить начальные условия и решить систему дифференциальных уравнений.
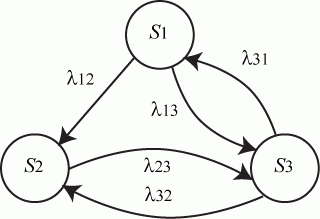
Пример 2.2. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рис. 2.3.
Решение
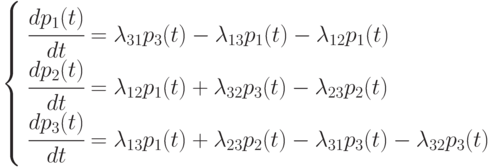
Очевидно, 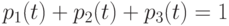 .
.
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера 2.2, можно задать такие начальные условия: 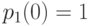 ,
, 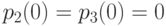 .
.
Однородный марковский процесс с непрерывным временем можно трактовать как процесс смены состояний под влиянием некоторого потока событий. То есть плотность вероятности перехода можно трактовать как интенсивность потока событий, переводящих систему из  -го состояния в
-го состояния в  -е. Такими потоками событий являются отказы техники, вызовы на телефонной станции, рождение и т. п.
-е. Такими потоками событий являются отказы техники, вызовы на телефонной станции, рождение и т. п.
При исследовании сложных объектов всегда интересует: возможен ли в исследуемой системе установившейся (стационарный) режим? То есть, как ведет себя система при 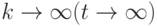 ? Существуют ли предельные значения
? Существуют ли предельные значения 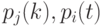 ? Как правило, именно эти предельные значения интересуют исследователя.
? Как правило, именно эти предельные значения интересуют исследователя.
Ответ на данный вопрос дает теорема Маркова.
Если для однородного дискретного марковского процесса с конечным или счетным числом состояний все 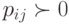 , то предельные значения
, то предельные значения  существуют и их значения не зависят от выбранного начального состояния системы.
существуют и их значения не зависят от выбранного начального состояния системы.
Применительно к непрерывным марковским процессам теорема Маркова трактуется так: если процесс однородный и из каждого состояния возможен переход за конечное время в любое другое состояние и число состояний счетно или конечно, то предельные значения 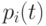 существуют и их значения не зависят от выбранного начального состояния.
существуют и их значения не зависят от выбранного начального состояния.
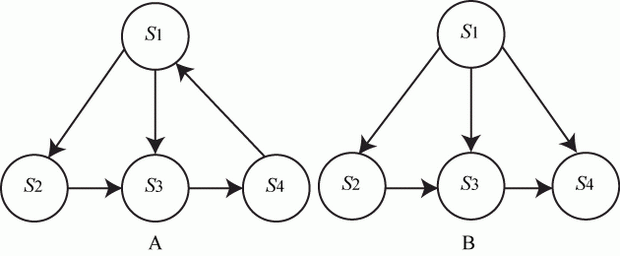
Например (рис. 2.4), в системе А стационарный режим есть, а в системе В стационарного режима нет: если система окажется в состоянии  она не сможет перейти ни в какое другое состояние.
она не сможет перейти ни в какое другое состояние.
2.3. Схема гибели и размножения
Часто в системах самого различного назначения протекают процессы, которые можно представить в виде модели "гибели и размножения".
Граф состояний такого процесса показан на рис. 2.5.
Особенностью модели является наличие прямой и обратной связей с каждым соседним состоянием для всех средних состояний; первое и последнее (крайние) состояния связаны только с одним "соседом" (с последующим и предыдущим состояниями соответственно).
Название модели - "гибель и размножение" - связано с представлением, что стрелки вправо означают переход к состояниям, связанным с ростом номера состояния ("рождение"), а стрелки влево - с убыванием номера состояний ("гибель").
Очевидно, стационарное состояние в этом процессе существует. Составлять уравнения Колмогорова нет необходимости, так как структура регулярна, необходимые формулы приводятся в справочниках, а также в рекомендованной литературе.
Для приведенных на рис. 2.5 обозначений формулы имеют вид:
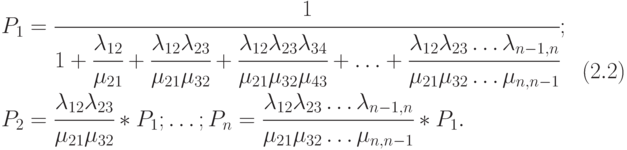
Пример 2.3. Имеется система из двух одинаковых и работающих параллельно компьютеров.
Требуется определить надежностные характеристики этой системы.
Решение
В этой системе возможны три состояния:
 - оба компьютера исправны;
- оба компьютера исправны;
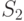 - один компьютер исправен, другой ремонтируется;
- один компьютер исправен, другой ремонтируется;
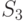 - оба компьютера неисправны и ремонтируются. Будем полагать, что процессы отказов и восстановлений - однородные марковские, одновременный выход из строя обоих компьютеров, как и одновременное восстановление двух отказавших компьютеров практически невозможно.
- оба компьютера неисправны и ремонтируются. Будем полагать, что процессы отказов и восстановлений - однородные марковские, одновременный выход из строя обоих компьютеров, как и одновременное восстановление двух отказавших компьютеров практически невозможно.
Поскольку компьютеры одинаковые, то с точки зрения надежности, неважно, какой именно компьютер неисправен в состоянии 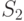 , важно, что один.
, важно, что один.
С учетом сказанного, ситуация моделируется схемой "гибели и размножения" (рис. 2.6).
На рис. 2.6:
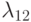 ,
, 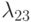 - интенсивности потоков отказов;
- интенсивности потоков отказов;
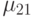 ,
,  - интенсивности потоков восстановлений.
- интенсивности потоков восстановлений.
Пусть среднее время безотказной работы каждого компьютера  , а среднее время восстановления одного компьютера
, а среднее время восстановления одного компьютера 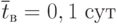 .
.
Тогда интенсивность отказов одного компьютера будет равна  , а интенсивность восстановления одного компьютера -
, а интенсивность восстановления одного компьютера -  .
.
В состоянии  работают оба компьютера, следовательно:
работают оба компьютера, следовательно:
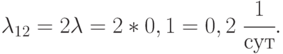
В состоянии 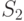 работает один компьютер, значит:
работает один компьютер, значит:
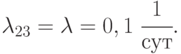
В состоянии 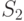 восстанавливается один компьютер, тогда:
восстанавливается один компьютер, тогда:
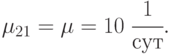
В состоянии 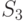 восстанавливаются оба компьютера:
восстанавливаются оба компьютера:
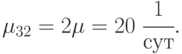
Используем зависимости (2.2). Вероятность состояния, когда обе машины исправны:
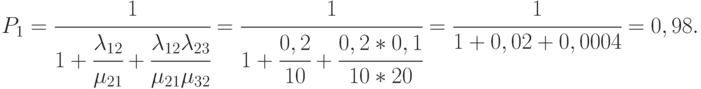
Вероятность второго состояния 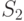 (работает один компьютер):
(работает один компьютер):
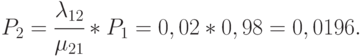
Аналогично вычисляется и 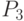 . Хотя найти
. Хотя найти 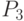 можно и так:
можно и так:
![\[{P_3} = 1 - \left( {{P_1} + {P_2}} \right) = 1 - \left( {0,98 + 0,0196} \right) = 1 - 0,9996 = 0,0004.\]](/sites/default/files/tex_cache/2ea0651cacbda328481dbfbce548e018.png)
Пример 2.4. В полосе объединения работают передатчики противника. Подразделение операторов-связистов армейской контрразведки ведет поиск передатчиков по их радиоизлучениям. Каждый оператор, обнаружив передатчик противника, следит за его частотой, при этом новым поиском не занимается. В процессе слежения частота может быть потеряна, после чего оператор снова осуществляет поиск.
Разработать математическую модель для определения эффективности службы подразделения операторов. Под эффективностью понимается среднее число обнаруженных передатчиков за установленный промежуток времени.
Решение
Будем считать, что наши операторы и радисты противника обладают высокой квалификацией, хорошо натренированы. Следовательно, можно принять, что интенсивности обнаружения частот передатчиков противника и потерь слежения - постоянны. Обнаружение частоты и ее потеря зависят только от того, сколько запеленговано передатчиков в настоящий момент и не зависят от того, когда произошло это пеленгование. Следовательно, процесс обнаружения и потерь слежения за частотами можно считать непрерывным однородным марковским процессом.
Исследуемое свойство этой системы пеленгации: загруженность операторов, что, очевидно, совпадает с числом обнаруженных частот.
Введем обозначения:
 - количество операторов;
- количество операторов;
 - количество передатчиков противника, полагаем
- количество передатчиков противника, полагаем 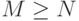 ;
;
 - среднее число операторов, ведущих слежение;
- среднее число операторов, ведущих слежение;
 - среднее число запеленгованных передатчиков;
- среднее число запеленгованных передатчиков;
 - интенсивность пеленгации передатчика противника одним оператором;
- интенсивность пеленгации передатчика противника одним оператором;
 - интенсивность потока потерь слежения оператором;
- интенсивность потока потерь слежения оператором;
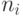 - текущая численность запеленгованных передатчиков
- текущая численность запеленгованных передатчиков  .
.
В системе пеленгации возможны следующие состояния:
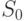 - запеленгованных передатчиков нет, поиск ведут
- запеленгованных передатчиков нет, поиск ведут  операторов, вероятность состояния
операторов, вероятность состояния 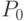 ;
;
 - запеленгован 1 передатчик, поиск ведут
- запеленгован 1 передатчик, поиск ведут 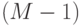 операторов, вероятность состояния
операторов, вероятность состояния 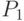 ;
;
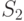 - запеленгованы 2 передатчика, поиск ведут
- запеленгованы 2 передатчика, поиск ведут 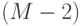 операторов, вероятность состояния
операторов, вероятность состояния  ;
;
…
 - запеленгованы
- запеленгованы 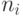 передатчиков, вероятность
передатчиков, вероятность 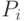 ;
;
…
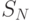 - запеленгованы
- запеленгованы  передатчиков, вероятность
передатчиков, вероятность 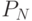 .
.
Цель моделирования -  - достигается вычислением:
- достигается вычислением:
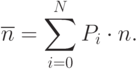
Как и в примере 2.3 полагаем, что одновременное обнаружение или потеря двух и более частот практически невозможно. Граф состояний системы показан на рис. 2.7.
Граф соответствует процессу "гибели и размножения", полносвязный, число состояний системы конечно, значит, установившийся режим, и предельные значения вероятностей в системе пеленгации существуют.
Пусть, к примеру, количество операторов 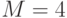 , а количество передатчиков противника
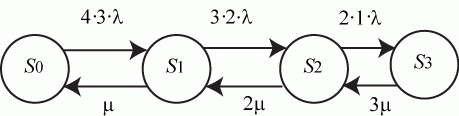
, а количество передатчиков противника 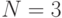 . В этом случае граф состояний имеет вид (рис. 2.8):
. В этом случае граф состояний имеет вид (рис. 2.8):
Для упрощения вычислений примем 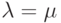 . Тогда для этой схемы "гибели и размножения" по зависимостям (2.2) имеем:
. Тогда для этой схемы "гибели и размножения" по зависимостям (2.2) имеем:
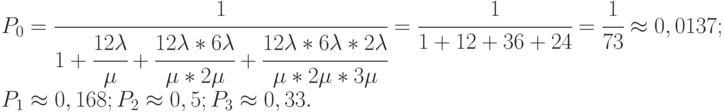
Окончательно:
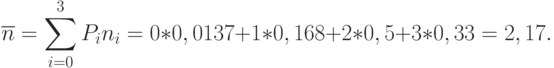
Таким образом, в условиях данного примера в среднем будут пеленговаться не менее двух передатчиков противника.
Непрерывный марковский процесс полностью определяется значениями плотностей вероятностей переходов 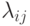 ,
, 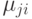 . Ранее был установлен их физический смысл как интенсивности потоков событий, переводящих систему из одного состояния в другое. Поток событий в однородных непрерывных марковских процессах характеризуется экспоненциальным законом распределения случайных интервалов времени между событиями. Такой поток называют простейшим или стационарным пуассоновским.
. Ранее был установлен их физический смысл как интенсивности потоков событий, переводящих систему из одного состояния в другое. Поток событий в однородных непрерывных марковских процессах характеризуется экспоненциальным законом распределения случайных интервалов времени между событиями. Такой поток называют простейшим или стационарным пуассоновским.
Простейший поток обладает свойствами:
- стационарности, что означает независимость характеристик потока от времени;
- ординарности, что означает практическую невозможность появления двух и более событий одновременно;
- отсутствия последействия, об этом говорилось в начале темы.