| Экстернат |
Криптосистемы
Криптография эллиптической кривой, моделирующая криптосистему Эль-Гамаля
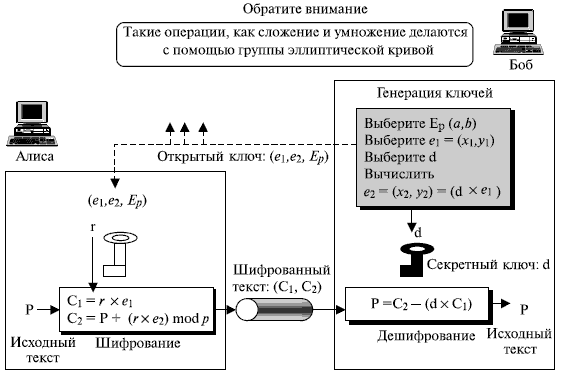
Для шифрования и дешифрования текстов, с помощью эллиптических кривых использовались несколько методов. Один из них состоит в том, чтобы моделировать криптосистему Эль-Гамаля, используя эллиптическую кривую в GF(p) или GF(2n), как это показано на рис. 15.7.
Генерация общедоступных и частных ключей
- Боб выбирает E (a,b) с эллиптической кривой в GF(p) или GF(2n).
- Боб выбирает точку на кривой, e1 (x 1, y1 ).
- Боб выбирает целое число d.
- Боб вычисляет
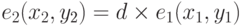 . Обратите внимание: умножение здесь означает, что многократное сложение и определяется как раньше.
. Обратите внимание: умножение здесь означает, что многократное сложение и определяется как раньше. - Боб объявляет E (a,b), e1 (x1, y1 ) и e2 (x2, y2) как свой открытый ключ доступа; он сохраняет d как секретный ключ.
Шифрование
Алиса выбирает P, точку на кривой, как ее исходный текст, P. Затем она вычисляет пару точек, направляет как зашифрованный текст:
Читатель может задаться вопросом, как произвольным исходным
C1 = r x e1 C2 = P + r x e2
Текстом может быть точка на эллиптической кривой. Это одна из основных проблем в применении эллиптической кривой для моделирования. Алиса должна использовать алгоритм, чтобы найти непосредственное соответствие между символами (или блоками текста) и точками на кривой.
Дешифрование
Боб, после получения C1 и C2, вычисляет P, исходный текст, используя следующую формулу:
P = C2 – (d x C1) Знак "минус" здесь означает сложение с инверсией.
Мы можем доказать, что P, вычисленный Бобом, — тот же, что передан Алисой, как это показано ниже:
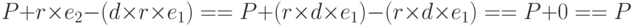
P, C 1, C2 и e2 — это точки на кривой. Обратите внимание, что результат сложения двух обратных точек на кривой — нулевая точка.
Пример 15.11
Вот очень тривиальный пример шифровки с использованием эллиптической кривой в GF (p).
- Боб выбирает E67 (2, 3) как эллиптическую кривую в GF (p).
- Боб выбирает e1 = (2, 22) и d = 4.
- Боб вычисляет e2 = (13, 45), где
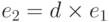 .
. - Боб публично объявляет кортеж (E, e1, e2).
- Алиса хочет передать исходный текст P = (24, 26) Бобу. Она выбирает r = 2.
- Алиса находит точку C1= (35, 1), где
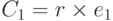 .
. - Алиса находит точку C2 = (21, 44), где
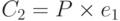 .
. - Боб получает C, и C2. Он использует
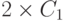 , (35, 1) и получает (23, 25).
, (35, 1) и получает (23, 25). - Боб инвертирует точку (23, 25) и получает точку (23, 42).
- Боб складывает (23, 42) с C2 = (21, 44) и получает первоначальный исходный текст P = (24, 26).
Сравнение
Ниже приводится краткое сравнение алгоритма Эль-Гамаля с его вариантом, использующим эллиптическую кривую.
a. Алгоритм Эль-Гамаля использует мультипликативную группу; вариант — эллиптическую группу.
b. Эти два члена в алгоритме Эль-Гамаля — числа в мультипликативной группе; при применении варианта — точки на эллиптической кривой.
c. Секретный ключ в каждом алгоритме — целое число.
d. Секретные числа, выбираемые Алисой в каждом алгоритме, — целые числа.
e. Возведение в степень в алгоритме Эль-Гамаля заменено умножением точки на константу.
f. Умножение в алгоритме Эль-Гамаля заменено сложением точек.
g. Инверсия в алгоритме Эль-Гамаля — мультипликативная инверсия в мультипликативной группе; инверсия —заменяется аддитивной инверсией точки на кривой.
h. Вычисление обычно легче в эллиптической кривой, потому что умножение проще, чем возведение в степень, сложение проще, чем умножение, и нахождение инверсии намного проще в группе эллиптической кривой, чем в мультипликативной группе.
Безопасность метода с использованием эллептической кривой
Чтобы расшифровать сообщение, Ева должна найти значение r или d.
a. Если Ева знает значение r, она может использовать  , чтобы найти точку P, относящуюся к исходному тексту. Но для того чтобы найти r, Ева должна решить уравнение
, чтобы найти точку P, относящуюся к исходному тексту. Но для того чтобы найти r, Ева должна решить уравнение 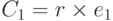 . Это значит — найти две точки на кривой, C1 и e1. Ева должна найти множитель, который создает C1 начиная с e1. Эта проблема известна как проблема логарифма эллиптической кривой, единственный известный метод решения этой проблемы —
. Это значит — найти две точки на кривой, C1 и e1. Ева должна найти множитель, который создает C1 начиная с e1. Эта проблема известна как проблема логарифма эллиптической кривой, единственный известный метод решения этой проблемы — 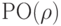 - алгоритм Поларда, который неосуществим, если задано большое r и p в GF (p) или большое n в GF(2n).
- алгоритм Поларда, который неосуществим, если задано большое r и p в GF (p) или большое n в GF(2n).
b. Если Ева знает значение d, она может использовать  , чтобы найти точку P, относящуюся к исходному тексту. Поскольку
, чтобы найти точку P, относящуюся к исходному тексту. Поскольку 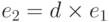 , это тот же самый тип проблемы, что и в предыдущем пункте. Ева знает значение e1 и e2 — она должна найти d.
, это тот же самый тип проблемы, что и в предыдущем пункте. Ева знает значение e1 и e2 — она должна найти d.
Размер модуля
Для того же самого уровня безопасности (затраты на вычисление) модуль n, может быть меньшим в эллиптической системе (ECC), чем в RSA. Например, ECC в GF(2n) с n, состоящим из 160 битов, может обеспечить тот же уровень безопасности, как RSA с n 1024 битов.