| Экстернат |
Криптосистемы
15.3. Криптосистемы на основе метода эллиптических кривых
Хотя RSA и Эль-Гамаль — безопасные асимметрично-ключевые криптографические системы, их безопасность обеспечивается ценой их больших ключей. Исследователи искали альтернативный метод, который дает тот же самый уровень безопасности с меньшими размерами ключей. Один из этих перспективных вариантов — криптосистема на основе метода эллиптических кривых (Elliptic Curve Cryptosystem — ECC). Система базируется на теории эллиптических кривых. Хотя глубокое рассмотрение этой теории находится вне задач и целей нашей книги, этот раздел сначала дает очень простое введение в три типа эллиптических кривых, а затем предлагает разновидности криптографических систем, которые используют некоторые из этих кривых.
Эллиптические кривые в вещественных числах
Эллиптические кривые, которые непосредственно не связаны с эллипсами, являются кубическими уравнениями двух переменных и обычно применяются для вычисления длины кривой в окружности эллипса. Общее уравнение для эллиптической кривой:
y2 + b1xy + b2y = x3 + a1x2 + a2x +a3
Эллиптические кривые в поле вещественных чисел используют специальный класс формы эллиптических кривых:
y2 = x3 + ax + b
В этом случае, если  , уравнение представляет несингулярную эллиптическую кривую ; в противоположном случае оно описывает сингулярную эллиптическую кривую. Для несингулярной эллиптической кривой уравнение x3 + ax + b = 0 имеет три отличных корня (вещественных или комплексных); для сингулярной уравнение x3 + ax + b = 0 не имеет трех отличных корней.
, уравнение представляет несингулярную эллиптическую кривую ; в противоположном случае оно описывает сингулярную эллиптическую кривую. Для несингулярной эллиптической кривой уравнение x3 + ax + b = 0 имеет три отличных корня (вещественных или комплексных); для сингулярной уравнение x3 + ax + b = 0 не имеет трех отличных корней.
В уравнении, как мы можем видеть, левая сторона ( y2 ) имеет степень 2, в то время как правая сторона имеет степень 3 ( x3 ). Это означает, что горизонтальная линия может пересекать кривую в трех точках, если все корни вещественные. Однако вертикальная линия может пересечь кривую самое большее в двух точках.
Пример 15.5
Рисунок 15.3 показывает две эллиптические кривые с уравнениями y2 = x3 – 4x и y2 = x 3 – 1. Оба уравнения несингулярны. Однако первое имеет три вещественных корня ( x = -2, x = 0, и x = 2 ), но второе — только один вещественный корень ( x = 1 ) и два мнимых.
Абелева группа
Определим абелеву (коммутативную) группу (см. лекции 5-6), использующую точки на эллиптической кривой. Кортеж P = (x1, y1) представляет точку на кривой, если x1 и y1 — координаты точки на кривой, которые удовлетворяют уравнению этой кривой. Например, точки P = (2,0; 0,0), Q = (0,0; 0,0), R = (–2,0; 0,0), S = (10,0;30,98), и T = (10,0; –30,98) – точки на кривой y2 = x3 – 4x. Обратите внимание, что каждая точка представлена двумя вещественными числами. По материалам лекций 5-6, для создания абелевой группы мы нуждаемся во множестве операций над множествами и пяти свойствах, которым удовлетворяют операции. В этом случае группа G = <E, +> — абелева.
Множество. Мы определим множество как точки на кривой, где каждая точка — пара вещественных чисел. Например, множество E для эллиптической кривой y2 = –x3 – 4x показано как
E = {(2,0; 0,0), (0,0; 0,0), (-2,0; 0,0), (10,0; 30,98), (10,0,-30,98)...}
Операция. Заданные свойства несингулярной эллиптической кривой позволяют нам определять операцию сложение точек на кривой. Однако мы должны помнить, что операция сложения здесь отличается от операции, которая была определена для целых чисел. Операция "сложение двух точек на кривой" проводится, чтобы получить другую точку на кривой.
R = P + Q, где P = (x1, y1), Q = (x2, y2), и R = (x3, y3)
Для того чтобы найти R на кривой, рассмотрим три случая, как это показано на рис. 15.4.
1. В первом случае две точки P = (x1, y1) и Q = (x2, y2) имеют различные x -координаты и y -координаты ( 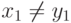 и
и 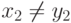 ), как это показано на рис. 15.4a. Линия, соединяющая P и Q, пересекает кривую в точке, обозначенной R. R есть отражение (-R) относительно y -оси. Координаты точки R, x3 и y3 могут быть найдены по наклону линии,
), как это показано на рис. 15.4a. Линия, соединяющая P и Q, пересекает кривую в точке, обозначенной R. R есть отражение (-R) относительно y -оси. Координаты точки R, x3 и y3 могут быть найдены по наклону линии, 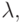 и затем можно вычислить значений x3 и y3, как показано ниже:
и затем можно вычислить значений x3 и y3, как показано ниже:

2. Во втором случае две точки совпадают (R = P + P), как показано на рис. 15.4b. Наклон линии и координаты точки R могут быть найдены, как показано ниже.
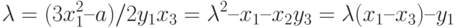
3. В третьем случае две точки — аддитивные инверсии друг друга, как это показано на рис. 15.4c. Если первая точка равна P = (x1, y1), а вторая точка равна Q = (x1, – y1), линия, соединяющая эти две точки, не пересекает кривую в третьей точке. Математики говорят в этом случае, что точка пересечения находится в бесконечности. Они определяют точку О (см. рис. 15.4с) как точку в бесконечности или нулевую точку, которая является аддитивным нейтральным элементом группы.
Свойства операции. Краткие определения свойств операции, как они обсуждались в лекциях 5-6:
- Замкнутость. Может быть доказано, что сложение двух точек, с использованием операции сложения, определенное в предыдущем разделе, создает другую точку на кривой.
- Ассоциативность. Может быть доказано, что (P + Q) + R = P + (Q + R).
- Коммутативность. группа, состоящая из точек несингулярной эллиптической кривой, — абелева группа. Может быть доказано, что P + Q = Q + P.
- Существование нейтрального элемента. Аддитивный нейтральный элемент в этом случае — нулевая точка. Другими словами, P + 0 = 0 + P.
- Существование инверсии. Каждая точка на кривой имеет инверсию. Инверсия точки — это ее отражение относительно оси x. Другими словами, точки P = (X1,Y1) И Q = (X1, – Y1) — инверсии друг друга; это означает, что P + Q = 0. Заметим, что нейтральный элемент — это инверсия самого себя.
Группа и поле
Обратите внимание, что предыдущие рассуждения касаются двух алгебраических структур: группа и поле. Группа определяет множество точек на эллиптической кривой и операции сложения точек. Поле определяет сложение, вычитание, умножение и деление, применяющие операции над вещественными числами, которые необходимы, чтобы найти сложение точек в группе.


