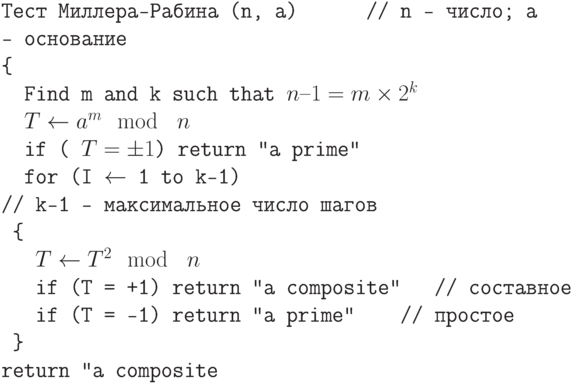| Экстернат |
Простые числа
Тест Миллера-Рабина
Тест Миллера-Рабина определения простого числа есть комбинация тестов Ферма и квадратного корня. Он элегантным способом находит сильное псевдопростое число (простое число с очень высокой вероятностью). В этом тесте мы записываем n–1 как произведение нечетного числа m и степени числа 2.

В тесте Ферма при основании a можно записать так, как это показано ниже.
Идея теста на простоту числа на основе Ферма
![a^{n-1}=a^{m\times2k}=[a^m]^2^k=[a^m]^2](/sites/default/files/tex_cache/abe86de5174255875794668c9299dcfe.png)
Другими словами, вместо того чтобы вычислять an-1 (mod n) в один шаг, мы можем сделать это в k + 1 шагов. Какое преимущество в таком применении? Преимущество заключается именно в том, что испытание квадратным корнем может быть выполнено на каждом шаге. Если квадратный корень показывает сомнительные результаты, мы останавливаемся и объявляем n составным номером. На каждом шаге мы обеспечиваем, что тест Ферма и испытание квадратным корнем удовлетворено на всех парах смежных шагов, если оно удовлетворительно (если результат равен 1).
Инициализация
Выберите основу и вычислите T = am, в который m = (n – 1) / 2k.
a. Если T равно +1 или –1, объявляют, что n — сильное псевдопростое число, и процесс останавливается. Мы говорим, что n прошел два испытания: тест Ферма и испытание квадратным корнем. Почему? Потому что если T равно  , то T станет 1 на следующем шаге и остается 1 до прохождения теста Ферма. Кроме того, T прошел испытание тестом квадратного корня, потому что T был бы равен 1 на следующем шаге и квадратный корень был бы равен 1 (на следующем шаге) и равен
, то T станет 1 на следующем шаге и остается 1 до прохождения теста Ферма. Кроме того, T прошел испытание тестом квадратного корня, потому что T был бы равен 1 на следующем шаге и квадратный корень был бы равен 1 (на следующем шаге) и равен  (на этом шаге).
(на этом шаге).
b. Если T равен другому значению, мы не уверены, является ли n простым числом или составным объектом, значит, процесс будет продолжаться на следующем шаге.
Шаг 1
Возводим T в квадрат.
a. Если результат равен +1, мы определенно знаем, что тест Ферма пройден, потому что T остается 1 для последующих испытаний. Испытание квадратным корнем, однако, не прошло. Поскольку T равно 1 на этом шаге и имело на предыдущем шаге другое значение, чем  (причина, почему мы не остановились на предыдущем шаге), n объявляют составным объектом, и процесс останавливается.
(причина, почему мы не остановились на предыдущем шаге), n объявляют составным объектом, и процесс останавливается.
b. Если результат равен (–1), мы знаем, что n в конечном счете пройдет тест Ферма. Мы знаем, что он пройдет испытание квадратным корнем, потому что T равно (–1) в этом шаге и станет 1 на следующем шаге. Мы объявляем n сильным псевдослучайным простым числом и останавливаем процесс.
c. Если T имеет еще какое-либо значение, мы не уверены, имеем ли мы дело с простым числом, и процесс продолжается на следующем шаге.
Шаги 2 до k–1
Этот шаг и все остальные шаги до k–1 такие же, как и шаг 1.
Этот шаг не является необходимым. Если мы достигли его и не приняли решение, он не поможет нам. Если результат этого шага (–1), значит, тест Ферма пройден, но поскольку результат предыдущего шага — не  , испытание квадратное корня не пройдено. После шага k – 1, если процесс не остановлен, мы объявляем, что n — составное.
, испытание квадратное корня не пройдено. После шага k – 1, если процесс не остановлен, мы объявляем, что n — составное.
Алгоритм 12.2 показывает псевдокод для теста Миллера-Рабина.
12.2. Псевдокод для теста Миллера-Рабина
Существует доказательство, что каждый раз, когда для числа проводится тест Миллера-Рабина, вероятность получить результат "не простое число" — 1/4. Если прошло m тестов (с m различными основаниями), вероятность, что тест выдаст не простое число — (1/4) m.
Пример 12.25
Проведите тест Миллера-Рабина к числу 561.
Решение
Используя основание 2, получим  , что означает, что m = 35, k = 4 и а = 2
, что означает, что m = 35, k = 4 и а = 2
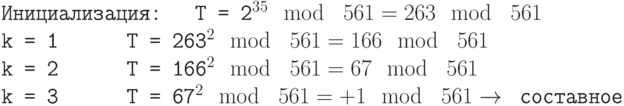
Пример 12.26
Мы уже знаем, что 27 — не простое число. Попробуем применить тест Миллера-Рабина.
Решение
Основание равно 2, тогда  , что означает m = 13, k = 1 и a = 2. В этом случае k – 1 = 0, и мы должны сделать только шаг инициализации:
, что означает m = 13, k = 1 и a = 2. В этом случае k – 1 = 0, и мы должны сделать только шаг инициализации:
T = 213 mod 27 = 11 mod 27. Однако поскольку алгоритм не делает ни одного цикла, вырабатывается решение "составной объект".
Пример 12.27
Мы знаем, что 61 — простое число; давайте посмотрим, что даст тест Миллера-Рабина
Решение
Мы используем основание 2.
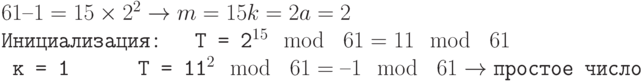
Обратите внимание, что последний результат — это 60 mod 61, но мы знаем, что 60 = –1 mod 61.
Рекомендованные тесты простоты чисел
Сегодня один из самых популярных тестов простоты чисел — комбинация теории делимости и тест Миллера-Рабина. При этом рекомендуются следующее шаги:
- Выбрать нечетное целое число, потому что все четные целые числа (кроме 2) — явно составные объекты.
- Сделать некоторые тривиальные испытания теории делимости на некоторых известных простых числах, таких как 3, 5, 7, 11, 13: так, чтобы убедиться, что вы не имеете дело с очевидным составным объектом. Если они не являются делителями при всех этих испытаниях, сделайте следующий шаг. Если выбранное число не прошло хотя бы один из этих тестов, вернитесь на один шаг и выберите другое нечетное число.
- Выбрать набор оснований для теста. Большое множество оснований предпочтительно.
- Сделать тест Миллера-Рабина на каждом из оснований. Если любой из них не проходит, вернитесь на один шаг и выберите другой нечетный номер. Если тесты прошли для всех оснований, объявите это число как сильное псевдопростое число.
Пример 12.28
Номер 4033 — составной объект (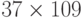 ). Это подтверждает рекомендованное испытание простоты чисел?
). Это подтверждает рекомендованное испытание простоты чисел?
Решение
1. Выполним проверку согласно теории делимости. Проверим сначала числа 2, 3, 5, 7, 11, 17 и 23 – не являются делителями числа 4033.
2. Выполним испытание Миллера-Рабина с основанием 2, тогда
 , что означает m = 63 и k = 6.
, что означает m = 63 и k = 6.
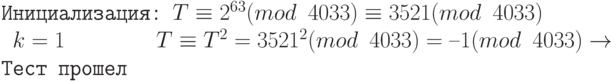
3. Но мы не удовлетворены. Мы продолжаем с другим основанием — 3.