| Экстернат |
Простые числа
Phi-функция Эйлера
Phi-функция Эйлера,  , которую иногда называют тотиентой Эйлера, играет очень важную роль в криптографии. Функция
, которую иногда называют тотиентой Эйлера, играет очень важную роль в криптографии. Функция  находит из ряда чисел 0,1…., n–1 числа, взаимно простые с n. Можно вспомнить из
"Модульная арифметика"
, что множество Zn* — числа, которые не больше чем n и взаимно простые с n. Функция
находит из ряда чисел 0,1…., n–1 числа, взаимно простые с n. Можно вспомнить из
"Модульная арифметика"
, что множество Zn* — числа, которые не больше чем n и взаимно простые с n. Функция  вычисляет число элементов этого множества. Ниже показано, как найти это значение:
вычисляет число элементов этого множества. Ниже показано, как найти это значение:
-
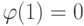 .
. -
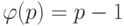 , если p — простое число.
, если p — простое число. -
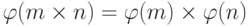 , если m и n — взаимно простые.
, если m и n — взаимно простые. -
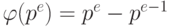 , если p — простое.
, если p — простое.
Мы можем объединить эти четыре правила, предназначенные для нахождения  .
.
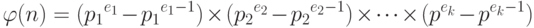
Очень важно заметить, что значение  для больших чисел может быть найдено, если может быть найдено число n и если n может быть представлено в виде разложения простых чисел. Другими словами, трудность нахождения
для больших чисел может быть найдено, если может быть найдено число n и если n может быть представлено в виде разложения простых чисел. Другими словами, трудность нахождения  зависит от трудности нахождения разложения n. Это рассматривается в следующем разделе.
зависит от трудности нахождения разложения n. Это рассматривается в следующем разделе.
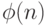 зависит от трудности нахождения разложения n.
зависит от трудности нахождения разложения n.Пример 12.7
Какое значение имеет  ?
?
Решение
Поскольку 13 — простое число, 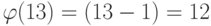 .
.
Пример 12.8
Какое значение имеет  ?
?
Решение
Мы можем использовать третье правило: 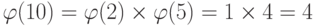 , поскольку 2 и 5 — простые числа.
, поскольку 2 и 5 — простые числа.
Пример 12.9
Какое значение имеет  ?
?
Решение
Мы можем записать  .
.
Тогда
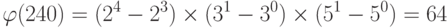
Пример 12.10
Можно ли утверждать, что 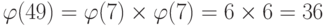 ?
?
Решение
Нет.
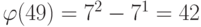
Пример 12.11
Какие числа являются элементами в Z14*?
Решение
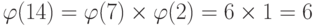 . Элементы – это 1, 3, 5, 9, 11 и 13.
. Элементы – это 1, 3, 5, 9, 11 и 13.
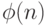 — четное.
— четное.Малая теорема Ферма
Малая теорема Ферма играет очень важную роль в теории чисел и криптографии. Ниже мы приводим две версии теоремы.
Первая версия
Первая версия говорит, что если p — простое число и a — целое число, такое, что p не является делителем a, тогда 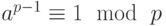 .
.
Вторая версия
Вторая версия вводит ограничивающие условие на a. Она утверждает, что если p — простое число и a — целое число, то  .
.
Приложения
Хотя мы будем рассматривать приложения этой теоремы позже в этой лекции, теорема очень полезна для того, чтобы решить некоторые проблемы.
Возведение в степень. Малая теорема Ферма иногда полезна для того, чтобы быстро найти решение при возведении в степень. Следующие примеры показывают это.
Пример 12.12
Найдите результат 610 mod 11.
Решение
Мы имеем  . Это первая версия малой теоремы Ферма, где p = 11.
. Это первая версия малой теоремы Ферма, где p = 11.
Пример 12.13
Найдите результат 312 mod 11.
Решение
Здесь степень (12) и модуль (11) не соответствуют условиям теоремы Ферма. Но, применяя преобразования, мы можем привести решение к использованию малой теоремы Ферма.

Мультипликативные инверсии. Очень интересное приложение теорема Ферма находит для некоторых мультипликативных инверсий, если модуль — простое число. Если p — простое число и a — целое число, такое, что p не является его делителем, тогда a-1mod p = ap-2 mod p. Это может быть легко доказано, если мы умножим обе стороны равенства на a и используем первую версию малой теоремы Ферма:
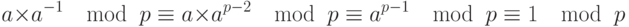
Это приложение позволяет не использовать расширенный алгоритм Евклида для нахождения мультипликативных инверсий.
Пример 12.14
Инверсии по модулю простого числа могут быть найдены без использования расширенного Евклидова алгоритма:
a. 8-1 mod 17 = 817-2 mod 17 = 815 mod 17 = 15 mod 17
b. 5 –1 mod 23 = 523-2 mod 23 = 521 mod 23 = 14 mod 23
c. 60101 mod 101 = 60101-2 mod 101 = 6099 mod 101 = 32 mod 101
d. 22 -1 mod 211 = 22 211-2 modа 211 = 22209 mod 211 = 48 mod 211
