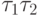| Дана ЛСА. y_H x_1\uparrow^1 x_2\uparrow^2 y_1\downarrow^2 y_3\downarrow^6 \rightharpoondown x_3\uparrow^5 y_5\downarrow^4 y_6 x_ |
Графический метод синтеза структурного автомата на триггерах
8.1 Этапы графического метода синтеза структурного автомата
Первые три этапа графического метода синтеза совпадают с табличным методом. Абстрактный автомат представлен в виде графа.
- Находим количество элементов памяти
![R >=]Log_2M[](/sites/default/files/tex_cache/57b0b35dee5eff6941145f4149856e1d.png) , (
, (  - число состояний абстрактного автомата) и кодируем состояния абстрактного автомата.
- число состояний абстрактного автомата) и кодируем состояния абстрактного автомата. - Кодируем входные и выходные сигналы.
- Структурный автомат представляем обобщенной схемой.
- Составление уравнений выходных функций.
Представляем закодированный граф абстрактного автомата, то есть вместо состояний автомата указываются соответствующие кодовые комбинации, а входные сигналы указываются на переходах своими логическими кодовыми комбинациями. Логические кодовые комбинации выходных сигналов 1 рода записываются на переходах, а сигналы 2 рода записываются как метки состояний (или внутри вершины графа). Причем для выходных функций следует указывать только те значения функций, которые принимают истинные значения, по которым составляются уравнения выходов.
- Составление уравнений функций возбуждения.
На закодированном графе на дугах перехода указываем функции возбуждения, которые соответствуют переключению триггеров, причем следует указывать только те значения функций, которые принимают истинные значения, по которым составляются уравнения функций возбуждения.
- Уравнения функций возбуждения и выходов минимизируются (по картам Карно, например) и по ним строится схема в заданном функционально - логическом базисе ({И, ИЛИ, НЕ}, {И-НЕ}, {ИЛИ-НЕ} ).
8.2 Пример графического метода синтеза структурного автомата
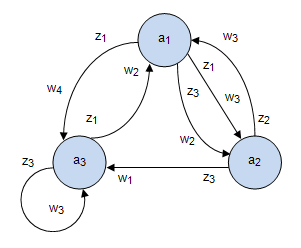
Пусть дан автомат Мили (рис.8.1). Выполним синтез структурного автомата на RS - триггерах.
- количество триггеров равно
![2 (R>=]Log_23[)](/sites/default/files/tex_cache/f8f6b11d6b4d7bbaf604300b2d7917d6.png) ). Состояния абстрактного автомата закодируем так, как показано в табл.8.1.
). Состояния абстрактного автомата закодируем так, как показано в табл.8.1.
- Кодируем входные и выходные сигналы , например, так как показано в табл.8.2 и табл.8.3.
- Структурный автомат представляем обобщенной схемой (рис.8.2).
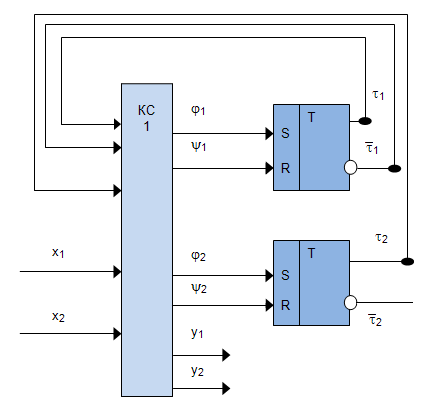
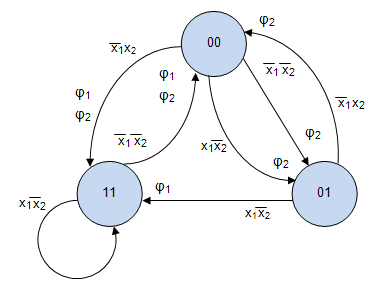
- Представляем закодированный граф абстрактного автомата (рис.8.3) то есть вместо состояний автомата указываются соответствующие кодовые комбинации, а входные сигналы указываются на переходах своими логическими кодовыми комбинациями. Логические кодовые комбинации выходных сигналов 1 рода записываются на переходах, а сигналы 2 рода записываются как метки состояний (или внутри вершины графа). Причем для выходных функций следует указывать только те значения функций, которые принимают истинные значения, по которым составляются уравнения выходов.
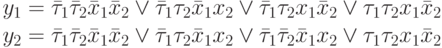
- Составление уравнений функций возбуждения для RS - триггера. На закодированном графе на дугах перехода указываем функции возбуждения:
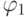 если 1-ый триггер переключился из 0 в 1;
если 1-ый триггер переключился из 0 в 1; 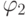 если 2-ой триггер переключился из 0 в 1;
если 2-ой триггер переключился из 0 в 1;  если 1-ый триггер переключился из 1 в 0;
если 1-ый триггер переключился из 1 в 0; 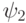 если 2-ой триггер переключился из 1 в 0; (рис.8.4).
если 2-ой триггер переключился из 1 в 0; (рис.8.4).
Уравнения функций возбуждения будут иметь вид:
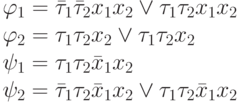
- Последний этап минимизации уравнений, построение схемы выполняется как и в предыдущих случаях синтеза.