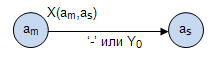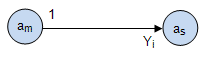| Дана ЛСА. y_H x_1\uparrow^1 x_2\uparrow^2 y_1\downarrow^2 y_3\downarrow^6 \rightharpoondown x_3\uparrow^5 y_5\downarrow^4 y_6 x_ |
Построение абстрактных автоматов по граф-схеме микропрограммы
4.1 Переход от ГСА МП к графу абстрактного автомата Мили
Переход осуществляется в два этапа. На первом этапе производится определение числа состояний путем разметки и отметки граф-схемы; на втором - определение графа автомата.
Правила разметки:
- Символом
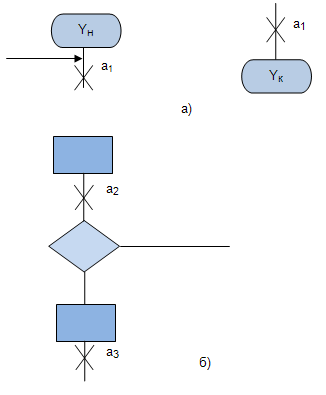
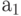 помечаем вход вершины следующей за начальным оператором в ГСА и вход конечной вершины. (рис.4.1,а).
помечаем вход вершины следующей за начальным оператором в ГСА и вход конечной вершины. (рис.4.1,а). - Символами
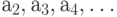 - входы вершин, следующих за операторными вершинами (рис.4.1,б).
- входы вершин, следующих за операторными вершинами (рис.4.1,б).
Если в результате разметки оказалось, что в одну и ту же вершину граф-схемы входит несколько размеченных стрелок, то им присваивается один и тот же символ. В дальнейшем символ 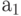 рассматривается как начальное состояние автомата, а символы
рассматривается как начальное состояние автомата, а символы 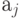 - как промежуточные состояния автомата. Таким образом, число состояний автомата опреде-ляется числом различающихся символов
- как промежуточные состояния автомата. Таким образом, число состояний автомата опреде-ляется числом различающихся символов 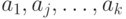
Переход от отмеченных граф-схем к графу автомата осуществ-ляется в следующем порядке.
Вершинами графа изображаются все состояния автомата и внутри кружков записываются символы  , то есть существующие метки на ГСА.
, то есть существующие метки на ГСА.
На граф-схеме микропрограммы отыскивается путь между двумя соседними состояниями 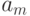 и
и 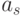 . Пути отображаются дугами. Возможно существование путей трех видов:
. Пути отображаются дугами. Возможно существование путей трех видов:
- Если этот путь содержит логические условия, то дуга, связывающая вершины
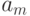 и
и 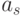 графа автомата, отмечается логической функцией
графа автомата, отмечается логической функцией  , значение которой определяет переход автомата из состояния
, значение которой определяет переход автомата из состояния 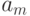 в состояние
в состояние 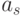 и оператором
и оператором 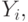 находящимся на пути между
находящимся на пути между 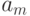 и
и 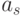 (рис.4.2).
(рис.4.2).
- Если этот путь содержит логические условия, то дуга, связывающая вершины
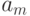 и
и 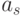 графа автомата, отмечается логической функцией, значение которой определяет переход автомата из состояния
графа автомата, отмечается логической функцией, значение которой определяет переход автомата из состояния 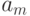 в состояние as и если на пути между
в состояние as и если на пути между 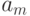 и
и 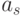 отсутствует операторная вершина, то этот факт отмечается символом '-' или символом
отсутствует операторная вершина, то этот факт отмечается символом '-' или символом 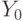 ( пустой оператор, пропуск такта) (рис.4.3);
( пустой оператор, пропуск такта) (рис.4.3);
- Если этот путь не содержит логические условия, то есть существует безусловный переход, то это путь третьего вида. Такой переход обозначается "1" вместо логической функции и оператором
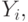 находящимся на пути между
находящимся на пути между 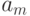 и
и 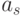 (рис.4.4).
(рис.4.4).
Построение графа автомата Мили по ГСА микропрограммы рассмотрим на примере ГСА, представленной на рис.4.5.
На первом этапе выполним разметку согласно указанным выше правилам. Получаем пять меток, выделенных красными крестиками на рис.4.5.
На втором этапе строим граф автомата Мура. Имеем пять вершин графа соответствующих пяти состояниям.
По ГСА находим все пути между соседними метками. Так из метки 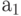 в метку
в метку  существует путь третьего типа, то есть безусловный переход. Этот путь проходит через операторную вершину, отмеченную сигналом
существует путь третьего типа, то есть безусловный переход. Этот путь проходит через операторную вершину, отмеченную сигналом 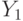 , который выносится на дугу перехода из состояния
, который выносится на дугу перехода из состояния 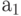 в состояние
в состояние  .
.
Рассмотрим пути, идущие от метки  . Всего их три. Первый путь из
. Всего их три. Первый путь из  в
в 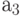 проходит через условную вершину
проходит через условную вершину 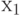 и операторную вершину
и операторную вершину 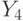 , то есть это путь первого вида, соответствующий переходу из состояния
, то есть это путь первого вида, соответствующий переходу из состояния  в состояние
в состояние 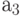 по условию
по условию 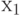 с выработкой выходного сигнала
с выработкой выходного сигнала 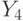 . Второй путь из
. Второй путь из  в
в  проходит через условные вершины
проходит через условные вершины 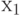 и
и 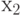 и операторную вершину
и операторную вершину 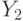 , то есть это путь первого вида, соответствующий переходу из состояния
, то есть это путь первого вида, соответствующий переходу из состояния  в состояние
в состояние  по условию
по условию 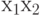 с выработкой выходного сигнала
с выработкой выходного сигнала 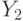 .
.
Третий путь из  в
в  проходит через условные вершины
проходит через условные вершины 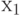 и
и 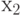 , и не проходит ни через какую операторную вершину, то есть это путь второго вида, соответствующий переходу из состояния
, и не проходит ни через какую операторную вершину, то есть это путь второго вида, соответствующий переходу из состояния  в состояние
в состояние  по условию
по условию 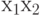 без выходного сигнала.
без выходного сигнала.
Рассмотрим пути, идущие от метки 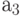 . Всего их два. Первый путь из
. Всего их два. Первый путь из 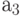 в
в 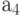 проходит через условную вершину
проходит через условную вершину  и операторную вершину
и операторную вершину 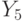 , то есть это путь первого вида, соответствующий переходу автомата из состояния
, то есть это путь первого вида, соответствующий переходу автомата из состояния 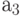 в состояние
в состояние 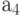 по условию
по условию  с выработкой выходного сигнала
с выработкой выходного сигнала 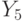 . Второй путь из
. Второй путь из 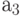 в
в 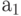 проходит через ту же условную вершины
проходит через ту же условную вершины 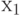 и не проходит ни через какую операторную вершину, то есть это путь второго вида, соответствующий переходу из состояния
и не проходит ни через какую операторную вершину, то есть это путь второго вида, соответствующий переходу из состояния 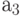 в состояние
в состояние 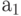 по условию
по условию  без выходного сигнала.
без выходного сигнала.
Из метки 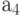 также существует два пути и оба второго типа без выходного сигнала: из
также существует два пути и оба второго типа без выходного сигнала: из 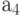 в
в 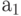 соответствующий переходу из состояния
соответствующий переходу из состояния 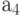 в состояние
в состояние 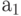 по условию
по условию 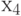 ; из
; из 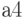 в
в  соответствующий переходу из состояния
соответствующий переходу из состояния 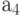 в состояние
в состояние  по условию
по условию 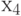 .
.
Из  существует один путь в
существует один путь в 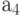 третьего вида, проходящий через операторную вершину
третьего вида, проходящий через операторную вершину 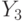 .
.
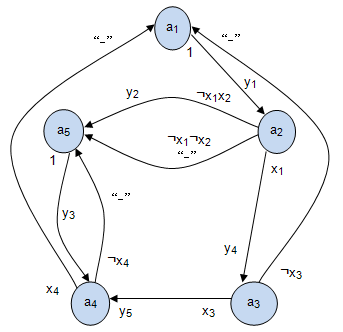
Результат построенного абстрактного автомата Мили показан на рис.4.6.
Если мы переобозначим сигналы на дугах, например заменив 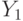 на
на 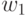 ,
, 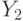 на
на  и т.д., а
и т.д., а 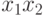 на
на 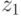 ,
, 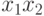 на
на 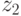 , и т.п., то получим абстрактный автомат Мили в привычном виде.
, и т.п., то получим абстрактный автомат Мили в привычном виде.