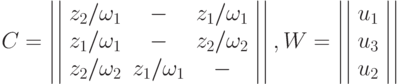| Дана ЛСА. y_H x_1\uparrow^1 x_2\uparrow^2 y_1\downarrow^2 y_3\downarrow^6 \rightharpoondown x_3\uparrow^5 y_5\downarrow^4 y_6 x_ |
Построение абстрактных автоматов по граф-схеме микропрограммы
4.2 Переход от ГСА МП к графу абстрактного автомата Мура
Переход осуществляется так же в два этапа. На первом этапе производится определение числа состояний путем разметки и отметки граф-схемы; на втором - определение графа автомата.
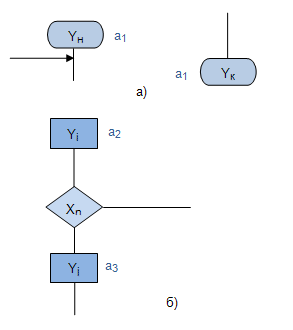
Правила разметки:
- Символом
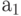 помечаем начальную и конечную вершины ГСА микропрограммы.
помечаем начальную и конечную вершины ГСА микропрограммы. - Символами
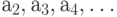 помечаем операторные вершины, (рис.4.7,б).
помечаем операторные вершины, (рис.4.7,б).
- Разные вершины ГСА должны быть помечены разными метками.
На втором этапе проводим построение графа автомата Мура, причем метки соответствуют вершинам графа, внутри которых записывается выходной сигнал, так как в автомате Мура выходной сигнал зависит только от состояния и не зависит от входного сигнала.
В результате анализа разметки видим, что между парами меток имеем пути второго и третьего вида. Каждому пути ставим соответствующий переход.
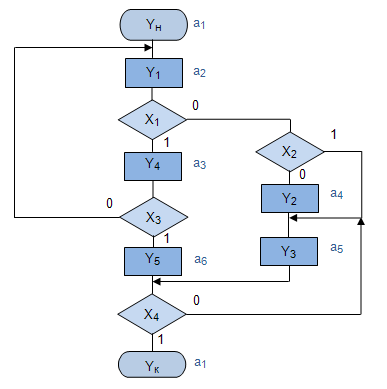
Построение автомата Мура рассмотрим на примере ГСА МП, представленной на рис.4.8.
На первом этапе выполним разметку согласно указанным выше правилам. Получаем шесть меток (рис.4.8).
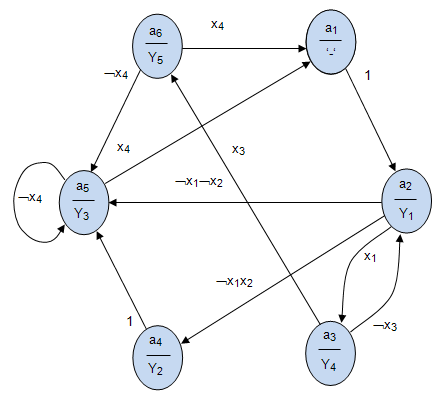
На втором этапе строим граф автомата Мили. Имеем шесть вершин графа соответствующих шести состояниям. Внутри каждой вершины записываем соответствующий выходной сигнал.
По ГСА находим все пути между соседними метками. Так из метки  в метку
в метку  существует один путь третьего типа, то есть безусловный переход. Этот путь изображается дугой перехода из состояния
существует один путь третьего типа, то есть безусловный переход. Этот путь изображается дугой перехода из состояния 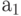 в состояние
в состояние  .
.
Рассмотрим пути, идущие от метки  . Всего их три. Первый путь из
. Всего их три. Первый путь из  в
в 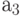 проходит через условную вершину
проходит через условную вершину 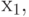 то есть это путь второго вида, соответствующий переходу из состояния
то есть это путь второго вида, соответствующий переходу из состояния  в состояние
в состояние 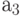 по условию
по условию 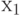 . Второй путь проходит через условные вершины
. Второй путь проходит через условные вершины 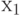 и
и 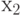 , то есть это тоже путь второго вида, соответствующий переходу из состояния
, то есть это тоже путь второго вида, соответствующий переходу из состояния  в состояние
в состояние 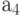 по условию
по условию 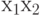 . Третий путь из
. Третий путь из  в
в  проходит через условные вершины
проходит через условные вершины 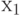 и
и 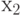 , то есть это путь второго вида, соответствующий переходу из состояния
, то есть это путь второго вида, соответствующий переходу из состояния  в состояние
в состояние  по условию
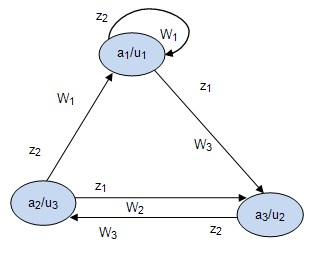
по условию 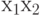 . Результат построенного абстрактного автомата Мили показан на рис. рис.4.9/
. Результат построенного абстрактного автомата Мили показан на рис. рис.4.9/
4.3 Абстрактный С-автомат (совмещенный автомат)
Очень часто в управляющих устройствах нужны сигналы обоих типов: первого рода как в абстрактном автомате Мили и второго рода как в абстрактном автомате Мура. В автомате Мили выходной сигнал зависит как от состояния, так и от входного сигнала и формируется в тот же дискретный интервал времени, в котором поступает входной сигнал (рис.4.10,а).
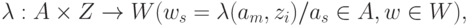
В автомате Мура выходной сигнал зависит только от состояния, и выдается все то время, когда автомат находится в этом состоянии (рис.4.10,б):

Совмещенный автомат или  - автомат таким образом содержит сигналы как первого рода, так и второго и описывается восьмеркой вида:
- автомат таким образом содержит сигналы как первого рода, так и второго и описывается восьмеркой вида:
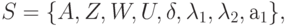
где  - множество состояний автомата;
- множество состояний автомата;
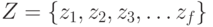 - множество входных сигналов;
- множество входных сигналов;
 - множество выходных сигналов 1 рода;
- множество выходных сигналов 1 рода;
 - множество выходных сигналов 2 рода;
- множество выходных сигналов 2 рода;
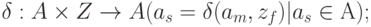
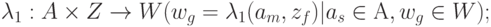
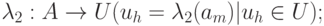

При графическом задании  - автомата на переходах указываются выходные сигналы 1 рода
- автомата на переходах указываются выходные сигналы 1 рода 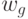 , а в вершинах выходные сигналы 2 рода
, а в вершинах выходные сигналы 2 рода 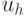 (рис.4.11).
(рис.4.11).
Явное задание  - автомата требует описание всех составляющих и выполняется так же как и для автоматов Мили и Мура.
- автомата требует описание всех составляющих и выполняется так же как и для автоматов Мили и Мура.
Табличное задание  - автомата состоит в представлении работы автомата двумя таблицами: таблицей переходов (табл.4.1) и таблицей выходов (табл.4.2), в которой в отличие от автомата Мили в верхней строке добавляются сигналы второго рода.
- автомата состоит в представлении работы автомата двумя таблицами: таблицей переходов (табл.4.1) и таблицей выходов (табл.4.2), в которой в отличие от автомата Мили в верхней строке добавляются сигналы второго рода.
Матричное задание  - автомата состоит в описании двумя матрицами аналогично матричному представлению автоматов Мили и Мура.
- автомата состоит в описании двумя матрицами аналогично матричному представлению автоматов Мили и Мура.