Представление геометрической информации

Геометрические примитивы

Под геометрическими примитивами понимают тот базовый набор геометрических фигур, который лежит в основе всех графических построений, причем эти фигуры должны образовывать "базис" в том смысле, что ни один из этих объектов нельзя построить через другие. Однако вопрос о том, что включать в набор геометрических примитивов, нельзя считать окончательно решенным в компьютерной графике. Например, количество примитивов можно свести к некоему минимуму, без которого нельзя обойтись, и этот минимум сводится к аппаратно реализованным графическим объектам. В этом случае базисный набор ограничивается отрезком, многоугольником и набором литер (символов).

Другая точка зрения состоит в том, что в набор примитивов необходимо включить гладкие кривые различного рода (окружности, эллипсы, кривые Безье), некоторые классы поверхностей и даже сплошные геометрические тела. В качестве трехмерных геометрических примитивов в таком случае предлагаются пространственные кривые, параллелепипеды, пирамиды, эллипсоиды. Но если такой расширенный набор примитивов связан с аппаратной реализацией, то возникает проблема перенесения программных приложений с одного компьютера на другой, поскольку такая аппаратная поддержка существует далеко не на всех графических станциях. Кроме того, при создании трехмерных геометрических примитивов программисты сталкиваются с проблемой их математического описания, а также разработки методов манипулирования такими объектами, поскольку те типы объектов, которые не попали в список базовых, надо уметь приближать с помощью этих примитивов.

Во многих случаях для аппроксимации сложных поверхностей используются многогранники, но форма граней может быть различной. Пространственный многоугольник с числом вершин больше трех не всегда бывает плоским, а в этом случае алгоритмы изображения многогранников могут привести к некорректному результату. Поэтому программист должен сам позаботиться о том, чтобы многогранник был описан правильно. В этом случае оптимальным выходом из положения является использование треугольников, поскольку треугольник всегда является плоским. В современной графике это, пожалуй, самый распространенный подход.

Но существует и альтернативное направление, которое называется конструктивной геометрией тел. В системах, использующих этот подход, объекты строятся из объемных примитивов с использованием теоретико- множественных операций (объединение, пересечение).

Любая графическая библиотека определяет свой набор примитивов. Так, например, широко распространенная интерактивная система трехмерной графики OpenGL включает в список своих примитивов точки (вершины), отрезки, ломаные, многоугольники (среди которых особо выделяются треугольники и четырехугольники), полосы (группы треугольников или четырехугольников с общими вершинами) и шрифты. Кроме того, в нее входят и некоторые геометрические тела: сфера, цилиндр, конус и др.

Понятно, что для изображения таких примитивов должны быть разработаны эффективные и надежные алгоритмы, поскольку они являются конструктивными элементами. Исторически сложилось так, что первые дисплеи были векторными, поэтому базовым примитивом был отрезок. Но, как уже было отмечено в первой главе нашего курса, самая первая интерактивная программа Sketchpad А.Сазерленда в качестве одного из примитивов имела прямоугольник, после чего этот объект уже традиционно входил в различные графические библиотеки.

Здесь мы рассмотрим такие примитивы, как вершина, отрезок, воксель и модели, строящиеся на их основе, а также функциональные модели.

Полигональные модели

Для этих пространственных моделей используются в качестве примитивов вершины (точки в пространстве), отрезки прямых (векторы), из которых строятся полилинии, полигоны и полигональные поверхности. Главным элементом описания является вершина, все остальные являются производными. В трехмерной декартовой системе координаты вершины определяются своими координатами (x,y,z), линия задается двумя вершинами, полилиния представляет собой незамкнутую ломаную линию, полигон - замкнутую ломаную линию. Полигон моделирует плоский объект и может описывать плоскую грань объемного объекта. Несколько граней составляют этот объект в виде полигональной поверхности - многогранник или незамкнутую поверхность ("полигональная сетка").

Рис. 4.1. Полигональные модели

В современной компьютерной графике векторно-полигональная модель является наиболее распространенной. Она применяется в системах автоматизированного проектирования, компьютерных играх, тренажерах, ГИС, САПР и т. д. Достоинства этой модели заключаются в следующем:

• Удобство масштабирования объектов.
• Небольшой объем данных для описания простых поверхностей.
• Аппаратная поддержка многих операций.

К числу недостатков полигональных моделей можно отнести то, что алгоритмы визуализации выполнения топологических операций (например, построение сечений) довольно сложны. Кроме того, аппроксимация плоскими гранями приводит к значительной погрешности, особенно при моделировании поверхностей сложной формы.

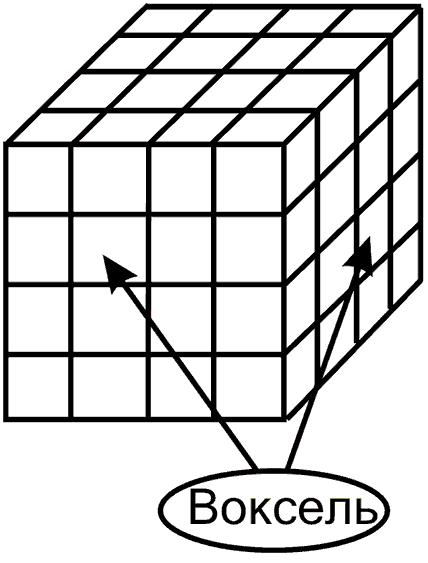
Воксельные модели

Воксельная модель - это представление объектов в виде трехмерного массива объемных (кубических) элементов. Само название "воксель" составлено из двух слов: volume element. Так же как и пиксель, воксель имеет свои атрибуты (цвет, прозрачность и т. п.). Полная прозрачность вокселя означает пустоту в соответствующей точке объема. Чем больше вокселей в определенном объеме и меньше их размер, тем точнее моделируются трехмерные объекты.

Рис. 4.2. Воксельная модель

Положительными чертами воксельной модели являются:

• Возможность представлять внутренность объекта, а не только внешний слой; простая процедура отображения объемных сцен.
• Простое выполнение топологических операций; например, чтобы показать сечение пространственного тела, достаточно воксели сделать прозрачными.

К ее недостаткам относятся:

• Большое количество информации, необходимое для представления объемных данных.
• Значительные затраты памяти, ограничивающие разрешающую способность, точность моделирования.
• Проблемы при увеличении или уменьшении изображения; например, с увеличением ухудшается разрешающая способность изображения.