| Отрезок пересекает левую и нижнюю границу клиппирующего окна.Чему могут быть равны коды его концов по алгоритму Сазерленда - Коэ |
Представление геометрической информации
Однородные координаты. Задание геометрических преобразований в однородных координатах с помощью матриц
В предыдущей главе описывались геометрические преобразования на
плоскости и в пространстве, а также было показано, как можно
использовать аппарат матриц для таких задач. Для преобразований на
плоскости применялись двумерные векторы и матрицы размерностью  . В
пространстве, соответственно, с этой же целью использовались
трехмерные векторы и матрицы
. В
пространстве, соответственно, с этой же целью использовались
трехмерные векторы и матрицы  . Но такой подход не позволяет задавать
с помощью матриц преобразования переноса и проекции. В связи с этим в
проективной геометрии был разработан аппарат, позволяющий
унифицировать все геометрические преобразования путем введения так
называемых однородных координат.
. Но такой подход не позволяет задавать
с помощью матриц преобразования переноса и проекции. В связи с этим в
проективной геометрии был разработан аппарат, позволяющий
унифицировать все геометрические преобразования путем введения так
называемых однородных координат.
Для пояснения такого подхода сначала рассмотрим случай двумерного
пространства. Каждая точка плоскости с координатами  может
одновременно рассматриваться как точка трехмерного пространства с
координатами
может
одновременно рассматриваться как точка трехмерного пространства с
координатами 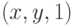 , т.е. как точка, лежащая на плоскости
, т.е. как точка, лежащая на плоскости 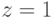 . С другой
стороны, каждой точке трехмерного пространства
. С другой
стороны, каждой точке трехмерного пространства 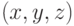 при условии
при условии 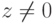 соответствует единственная точка этой же плоскости
соответствует единственная точка этой же плоскости 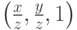 . При этом
получается, что каждой точке плоскости
. При этом
получается, что каждой точке плоскости 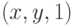 соответствует прямая,
проходящая через начало координат, т. е. устанавливается взаимно
однозначное соответствие между точками плоскости и множествами
соответствует прямая,
проходящая через начало координат, т. е. устанавливается взаимно
однозначное соответствие между точками плоскости и множествами 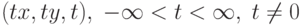 .
.
Если теперь рассматривать точку плоскости как принадлежащую трехмерному пространству, то ее двумерные преобразования можно будет
описывать с помощью матриц  , причем можно будет задавать таким
способом не только повороты и масштабирование, но и сдвиги и проекции
(как ортографические, так и центральные).
, причем можно будет задавать таким
способом не только повороты и масштабирование, но и сдвиги и проекции
(как ортографические, так и центральные).
Поворот на угол  относительно начала координат можно осуществить с
помощью новой матрицы поворота:
относительно начала координат можно осуществить с
помощью новой матрицы поворота:

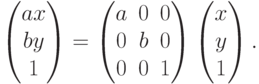
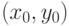 также можно задать с помощью матрицы:
также можно задать с помощью матрицы: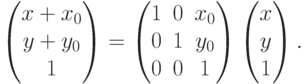
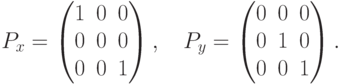
Перейдем теперь к трехмерному пространству. Каждой точке 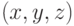 будем
ставить в соответствие точку четырехмерного пространства
будем
ставить в соответствие точку четырехмерного пространства 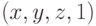 , а для
выполнения основных преобразований будем использовать матрицы
размерностью
, а для
выполнения основных преобразований будем использовать матрицы
размерностью  . Строятся они совершенно аналогично тому, как это
делалось в двумерном случае. Матрица сдвига на вектор
. Строятся они совершенно аналогично тому, как это
делалось в двумерном случае. Матрица сдвига на вектор  имеет вид
имеет вид
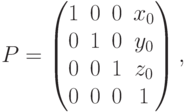
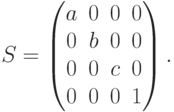
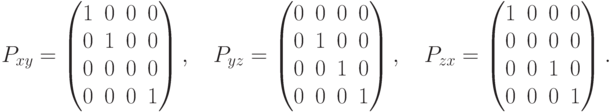
Матрица поворота относительно оси 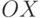 на угол
на угол  выглядит следующим образом:
выглядит следующим образом:
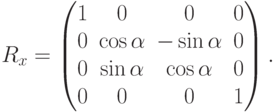

Путем объединения приведенных элементарных преобразований можно построить и более сложные. В третьей главе мы использовали произведение простых матриц вращения для построения матрицы поворота относительно произвольной оси. Приведем один пример.
Пусть в пространстве заданы два отрезка -  и
и  . Будем строить
матрицу преобразования, переводящую первый отрезок во второй. Это
преобразование разложим на следующие элементарные действия.
. Будем строить
матрицу преобразования, переводящую первый отрезок во второй. Это
преобразование разложим на следующие элементарные действия.
- Сдвиг, перемещающий точку
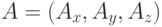 в точку
в точку 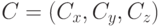 .
. - Сдвиг начала координат в эту же точку.
- Если отрезки неколлинеарны:
- Масштабирование с целью выравнивания длины отрезков.
- Возвращение начала координат в исходную точку.
Каждое из этих преобразований реализуется с помощью матрицы, а полное преобразование можно выполнить, используя произведение матриц.
Использование матриц очень удобно для выполнения преобразований в
пространстве, хотя в некоторых случаях это приводит к избыточному
числу выполняемых операций. Например, поворот одной точки в
пространстве относительно координатной оси 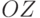 с помощью матриц в
однородных координатах требует 16 операций умножения и 12 операций
сложения. В то же время он легко может быть выполнен с помощью формул
преобразования
с помощью матриц в
однородных координатах требует 16 операций умножения и 12 операций
сложения. В то же время он легко может быть выполнен с помощью формул
преобразования
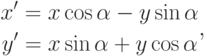
Вопросы и упражнения
- Какие геометрические объекты считаются примитивами?
- Какие требования предъявляются к набору геометрических примитивов?
- В какой программе впервые в качестве геометрического примитива использовался прямоугольник?
- Что такое объектная система координат?
- Что такое система координат наблюдателя?
- Соответствуют ли размеры объектов в системе координат наблюдателя их реальным размерам?
- Что такое картинная плоскость?
- Как называется операция перехода от трехмерной системы координат к двумерной?
- Что происходит при перенесении изображения с картинной плоскости на экран?
- Чем отличаются однородные координаты точки от обычных декартовых координат?
- С какой целью вводятся однородные координаты?
- Сколько элементарных действий требуется для совмещения двух отрезков в пространстве?
- Всегда ли использование матриц для выполнения преобразований в пространстве эффективней, чем другие способы их реализации?
