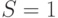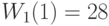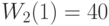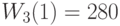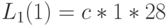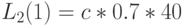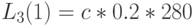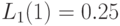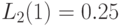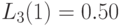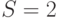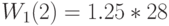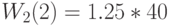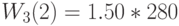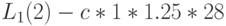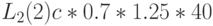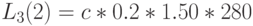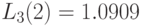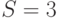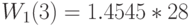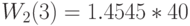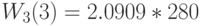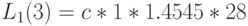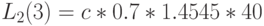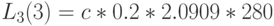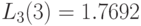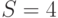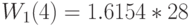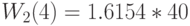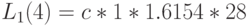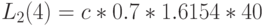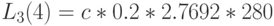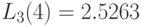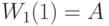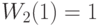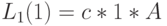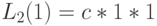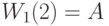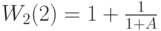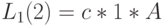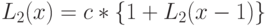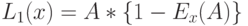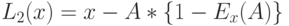| Стоимость "обучения" |
Сети очередей
МУЛ-алгоритм
Алгоритм средней величины (MVA - Mean Value Algorithm ) - это алгоритм для вычисления критериев качества работы сетей очередей. Он изящным образом сочетает два главных результата в теории организации очереди: теорему прибытия (8.27) и закон (формулу) Литтла (5.20). Алгоритм был сначала опубликован Lavenberg и Reiser (1980 [72]).
Мы рассматриваем сеть организации очереди с  узлами и
узлами и  клиентами (все принадлежат одной цепочке). Относительные нагрузки узлов обозначены
клиентами (все принадлежат одной цепочке). Относительные нагрузки узлов обозначены 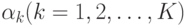 . Алгоритм рекурсивный по числу заявок от клиентов сети, то есть сеть с
. Алгоритм рекурсивный по числу заявок от клиентов сети, то есть сеть с 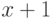 заявкой от клиентов получается из сети, обслуживающей
заявкой от клиентов получается из сети, обслуживающей  заявок.
заявок.
Примем, что среднее число заявок оот клиентов в узле  равно
равно 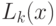 , где
, где  - общее количество клиентов в сети. Очевидно, что:
- общее количество клиентов в сети. Очевидно, что:
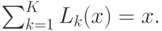 |
( 14.11) |
Алгоритм выполняется рекурсивно за два шага.
Шаг 1.
Увеличьте число заявок от клиентов от  до
до 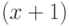 . Согласно теореме прибытия,
. Согласно теореме прибытия, 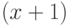 -ый клиент поступит в систему, когда система с
-ый клиент поступит в систему, когда система с  клиентами находится в статистическом равновесии. Следовательно, среднее время пребывания (время ожидания + время обслуживания) в узле
клиентами находится в статистическом равновесии. Следовательно, среднее время пребывания (время ожидания + время обслуживания) в узле  :
:
-
для M/M/1, M/G/1-PS M/G/1-LCFS-PR
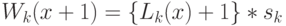 .
. -
для
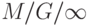 :
: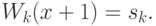
где
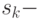 среднее время обслуживания в узле
среднее время обслуживания в узле  , который имеет
, который имеет 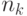 приборов. Для вычисления средних времен ожидания мы можем принять
приборов. Для вычисления средних времен ожидания мы можем принять 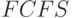 -дисциплину организации очереди.
-дисциплину организации очереди.
Шаг 2.
Используя формулу Литтла (  ), которая применима для всех систем в статистическом равновесии, для узла
), которая применима для всех систем в статистическом равновесии, для узла  мы получим:
мы получим:

где 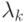 - относительная интенсивность поступления заявок к узлу
- относительная интенсивность поступления заявок к узлу  . Константа нормализации c получена, исходя из общего количества клиентов:
. Константа нормализации c получена, исходя из общего количества клиентов:
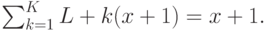 |
( 14.13) |
За эти два шага мы выполнили рекурсию от  до
до 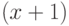 заявок. Для
заявок. Для  нет никакого времени ожидания в системе, и
нет никакого времени ожидания в системе, и 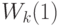 равняется среднему времени обслуживания
равняется среднему времени обслуживания 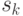 . Ниже был показан
. Ниже был показан 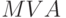 -алгоритм для одного узла обслуживания, но довольно просто делать вывод для узлов или с несколькими обслуживающими приборами или с бесконечным числом обслуживающих приборов.
-алгоритм для одного узла обслуживания, но довольно просто делать вывод для узлов или с несколькими обслуживающими приборами или с бесконечным числом обслуживающих приборов.
Пример 14.4.3: Модель с центральным обслуживающим прибором
Применим MVA -алгоритм к модели с центральным обслуживающим прибором (Пример 14.4.2). Относительная интенсивность поступления:
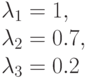
Естественно, что результат идентичен тому, который получен при применении алгоритма свертывания. Время пребывания на каждом узле (выраженное через единицу времени):
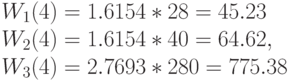
Пример 14.4.4: MVA-АЛГОРИТМ, в приложении к модели Пальма (восстановления машин)
Мы рассматриваем модель Пальма восстановления машин с  источниками, конечным временем раздумья и центральным процессором (время обслуживания равняется одной единице времени). Как было упомянуто в секции 12.5.2, эта модель эквивалентна системе с потерями Эрланга с
источниками, конечным временем раздумья и центральным процессором (время обслуживания равняется одной единице времени). Как было упомянуто в секции 12.5.2, эта модель эквивалентна системе с потерями Эрланга с  серверами и предложенной нагрузкой
серверами и предложенной нагрузкой  . Это также закрытая сеть организации очереди с двумя узлами и
. Это также закрытая сеть организации очереди с двумя узлами и  клиентами в одной цепочке. Если мы применяем MVA -алгоритм к этой системе, то получаем рекурсивную формулу Эрланга - B-формулу (7.29). Относительная интенсивность посещения идентична той с которой клиент соответственно посещает первый или второй узел:
клиентами в одной цепочке. Если мы применяем MVA -алгоритм к этой системе, то получаем рекурсивную формулу Эрланга - B-формулу (7.29). Относительная интенсивность посещения идентична той с которой клиент соответственно посещает первый или второй узел: 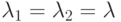 .
.
Мы знаем, что длина очереди в терминалах (узел 1) равна обслуженной нагрузке, измеренной в Эрлангах - в системе, и что все другие заявки клиенты находятся в центральном процессоре (узел 2). Мы, таким образом, имеем:
Из этого получаем нормировочную константу 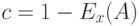 и находим для
и находим для 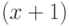 того клиента:
того клиента:
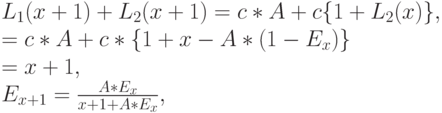
потому что  . Это рекурсивная формула для системы B-Эрланга.
. Это рекурсивная формула для системы B-Эрланга.
BCMP-сети очередей
В 1975 г. вторая модель Джексона была далее обобщена Baskett, Chandy, Muntz и Palacios (1975 [4]). Они показали, что сети очередей с более чем одним типом клиентов также имеют мультипликативную форму, при условии, что:
- каждый узел имеет симметричную систему организации очереди см. секцию 14.2: Пуассоновский поток вызовов
 Пуассоновский процесс освобождения);
Пуассоновский процесс освобождения); - заявки от клиентов классифицированы в
 цепочки. Каждая цепочка характеризуется своим собственным средним временем обслуживания
цепочки. Каждая цепочка характеризуется своим собственным средним временем обслуживания  и вероятностями перехода
и вероятностями перехода 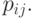 Кроме того, после окончания обслуживания в узле клиент может переходить из одной цепочки к другой с некоторой вероятностью. Имеется одно ограничение: если дисциплина организации очереди в узле -
Кроме того, после окончания обслуживания в узле клиент может переходить из одной цепочки к другой с некоторой вероятностью. Имеется одно ограничение: если дисциплина организации очереди в узле -  (включая
(включая 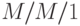 ), то среднее время обслуживания должно быть идентично для всех цепочек в узле.
), то среднее время обслуживания должно быть идентично для всех цепочек в узле.
BCMP -сети могут быть рассчитаны с помощью многомерного алгоритма свертывания и многомерного MVA -алгоритма.
Смешанные сети очередей (открытые и закрытые) рассчитываются сначала путем вычисления нагрузки от открытых цепочек в каждом узле. Эту нагрузку нужно обслуживать так, чтобы соблюдалось статистическое равновесие.
Производительность этих узлов уменьшается на эту нагрузку, и закрытая сеть очередей рассчитывается уже с меньшей производительностью. Так что главная проблема состоит в расчете закрытых сетей. Для этого мы можем использовать много алгоритмов, среди которых самыми важными являются алгоритмы свертывании и Алгоритм Средней величины ( MVA - Mean Value Algorithm ).