| Выполнение каких функций не изменяет позицию указателя в файле? |
Рекурсия и рекурсивные алгоритмы
Пример 2. Задача о нахождении центра тяжести выпуклого многоугольника.
Выпуклый многоугольник задан на плоскости координатами своих вершин. Найдите его центр тяжести.
Разработаем рекурсивную триаду.
Параметризация: x, y – вещественные массивы, в которых хранятся координаты вершин многоугольника; n – это число вершин многоугольника, по условию задачи, n>1 так как минимальное число вершин имеет двуугольник (отрезок).
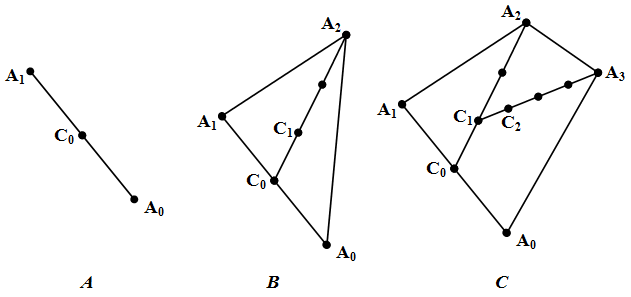
База рекурсии: для n=2 в качестве многоугольника рассматривается отрезок, центром тяжести которого является его середина (рис. 34А). При этом середина делит отрезок в отношении 1 : 1. Если координаты концов отрезка заданы как (x0,y0) и (x1,y1), то координаты середины вычисляются по формуле:
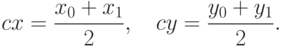
Декомпозиция: если n>2, то рассмотрим последовательное нахождение центров тяжести треугольника, четырехугольника и т.д.
Для n=3 центром тяжести треугольника является точка пересечения его медиан, которая делит каждую медиану в отношении 2 : 1, считая от вершины. Но основание медианы – это середина отрезка, являющегося стороной треугольника. Таким образом, для нахождения центра тяжести треугольника необходимо: найти центр тяжести стороны треугольника (отрезка), затем разделить в отношении 2 : 1, считая от вершины, отрезок, образованный основанием медианы и третьей вершиной (рис. 34B).
Для n=4 центром тяжести четырехугольника является точка, делящая в отношении 3 : 1, считая от вершины, отрезок: он образован центром тяжести треугольника, построенного на трех вершинах, и четвертой вершиной (рис. 34C).
Таким образом, для нахождения центра тяжести n -угольника необходимо разделить в отношении (n-1): 1, считая от вершины, отрезок: он образован центром тяжести (n-1) -угольника и n -ой вершиной рассматриваемого многоугольника. Если концы отрезка заданы координатами вершины (xn,yn) и центра тяжести (n-1) -угольника (cxn-1,cyn-1), то при делении отрезка в данном отношении получаем координаты:
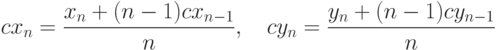
#include "stdafx.h"
#include <iostream>
using namespace std;
#define max 20
void centr(int n,float *x, float *y, float *c);
int _tmain(int argc, _TCHAR* argv[]){
int m, i=0;
FILE *f;
if ( ( f = fopen("in.txt", "r") ) == NULL )
perror("in.txt");
else {
fscanf(f, "%d",&m);
printf("\n%d",m);
if ( m < 2 || m > max ) //вырожденный многоугольник
printf ("Вырожденный многоугольник");
else {
float *px,*py,*pc;
px = new float[m];
py = new float[m];
pc = new float[2];
pc[0] = pc[1] = 0;
while(i<m) {
fscanf(f, "%f %f",&px[i], &py[i]);
printf("\n%f %f",px[i], py[i]);
i++;
}
centr(m,px,py,pc);
printf ("\nЦентр тяжести имеет координаты:
(%.4f, %.4f)",pc[0],pc[1]);
delete [] pc;
delete [] py;
delete [] px;
}
fclose(f);
}
system("pause");
return 0;
}
void centr(int n,float *x, float *y, float *c){
//n - количество вершин,
//x,y - координаты вершин,
//c - координаты центра тяжести
if(n==2){ //база рекурсии
c[0]=(x[0]+x[1])/2;
c[1]=(y[0]+y[1])/2;
}
if(n>2) { //декомпозиция
centr(n-1,x,y,c);
c[0]= (x[n-1] + (n-1)*c[0])/n;
c[1]= (y[n-1] + (n-1)*c[1])/n;
}
}Характеристиками рассматриваемого метода оценки алгоритма будут следующие величины.
Однако в данном случае для более достоверной оценки необходимо учитывать емкостные характеристики алгоритма.