| Выполнение каких функций не изменяет позицию указателя в файле? |
Одномерные массивы: задачи сортировок элементов массива
Цель лекции: изучить понятия и классификацию алгоритмов сортировок массивов, реализацию алгоритмов простых сортировок и научиться решать задачи на сортировку одномерных массивов с помощью алгоритмов простых сортировок в языке C++.
Задача сортировки является такой же базовой, как задача поиска. В практических условиях эти задачи взаимосвязаны. Решению проблем, связанных с сортировкой, посвящено множество фундаментальных научных исследований, разработано множество алгоритмов.
В общем случае сортировку следует понимать как процесс перегруппировки заданного множества объектов в определенном порядке. Часто при сортировке больших объемов данных нецелесообразно переставлять сами элементы, поэтому для решения задачи выполняется упорядочивание элементов по индексам. То есть индексы элементов выстраивают в такой последовательности, что соответствующие им значения элементов оказываются отсортированными по условию задачи.
Сортировка применяется для облегчения поиска элементов в упорядоченном множестве. Задача сортировки одна из фундаментных в программировании.
Сортировка – это упорядочивание набора однотипных данных по возрастанию или убыванию.
Чаще всего при сортировке данных лишь часть их используется в качестве ключа сортировки. Ключ сортировки – это часть данных, определяющая порядок элементов. Таким образом, ключ участвует в сравнениях, но при обмене элементов происходит перемещение всей структуры данных. Например, в списке почтовой рассылки в качестве ключа может использоваться почтовый индекс, но сортируется весь адрес. При решении задач сортировок массивов ключ и данные совпадают.
Для того, чтобы отсортировать данные, можно вызывать стандартную функцию qsort(), входящую в библиотеку С++. Однако различные подходы к сортировке обладают разными характеристиками. Несмотря на то, что некоторые способы сортировки могут быть в среднем лучше, чем другие, ни один алгоритм не является идеальным для всех случаев.
Использование функции qsort() не является универсальным решением для всех задач сортировки. Во-первых, функцию общего назначения, такую как qsort(), невозможно применить во всех ситуациях. Например, данная функция сортирует только массивы в памяти и не может сортировать данные, хранящиеся в связанных списках. Во-вторых, qsort() – параметризованная функция, благодаря чему она может обрабатывать широкий набор типов данных, но вследствие этого она работает медленнее, чем эквивалентная функция, рассчитанная на какой-то один тип данных. В-третьих, алгоритм быстрой сортировки, примененный в функции qsort(), может оказаться не самым эффективным алгоритмом в некоторых конкретных ситуациях.
Оценка алгоритмов сортировки
Существует множество различных алгоритмов сортировки. Все они имеют свои положительные и отрицательные стороны. Перечислим общие критерии оценки алгоритмов сортировки.
- Скорость работы алгоритма сортировки. Она непосредственно связана с количеством сравнений и количеством обменов, происходящих во время сортировки, причем обмены занимают больше времени. Сравнение происходит тогда, когда один элемент массива сравнивается с другим; обмен происходит тогда, когда два элемента меняются местами. Время работы одних алгоритмов сортировки растет экспоненциально, а время работы других логарифмически зависит от количества элементов.
- Время работы в лучшем и худшем случаях. Оно имеет значение при анализе выполнения алгоритма, если одна из краевых ситуаций будет встречаться довольно часто. Алгоритм сортировки зачастую имеет хорошее среднее время выполнения, но в худшем случае он работает очень медленно.
- Поведение алгоритма сортировки. Поведение алгоритма сортировки называется естественным, если время сортировки минимально для уже упорядоченного списка элементов, увеличивается по мере возрастания степени неупорядоченности списка и максимально, когда элементы списка расположены в обратном порядке. Объем работы алгоритма оценивается количеством производимых сравнений и обменов.
Различные сортировки массивов отличаются по быстродействию. Существуют простые методы сортировок, которые требуют порядка n*n сравнений, где n – количество элементов массива и быстрые сортировки, которые требуют порядка n*ln(n) сравнений. Простые методы удобны для объяснения принципов сортировок, т.к. имеют простые и короткие алгоритмы. Усложненные методы требуют меньшего числа операций, но сами операции более сложные, поэтому для небольших массивов простые методы более эффективны.
Простые методы сортировки можно разделить на три основные категории:
- сортировка методом "пузырька" (простого обмена);
- сортировка методом простого выбора (простой перебор);
- сортировка методом простого включения (сдвиг-вставка, вставками, вставка и сдвиг).
Сортировка методом "пузырька" (простого обмена)
Самый известный алгоритм – пузырьковая сортировка (bubble sort, сортировка методом пузырька или просто сортировка пузырьком). Его популярность объясняется интересным названием и простотой самого алгоритма.
Алгоритм попарного сравнения элементов массива в литературе часто называют "методом пузырька", проводя аналогию с пузырьком, поднимающимся со дна бокала с газированной водой. По мере всплывания пузырек сталкивается с другими пузырьками и, сливаясь с ними, увеличивается в объеме. Чтобы аналогия стала очевидной, нужно считать, что элементы массива расположены вертикально друг над другом, и их нужно так упорядочить, чтобы они увеличивались сверху вниз.
Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает – массив отсортирован. При проходе алгоритма элемент, стоящий не на своём месте, "всплывает" до нужной позиции ( рис. 12.1).
//Описание функции сортировки методом "пузырька"
void BubbleSort (int k,int x[max]) {
int i,j,buf;
for (i=k-1;i>0;i--)
for (j=0;j<i;j++)
if (x[j]>x[j+1]) {
buf=x[j];
x[j]=x[j+1];
x[j+1]=buf;
}
}В пузырьковой сортировке количество сравнений всегда одно и то же, поскольку два цикла for повторяются указанное количество раз независимо от того, был список изначально упорядочен или нет. Это значит, что алгоритм пузырьковой сортировки всегда выполняет
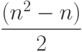
Пузырьковая сортировка имеет такую особенность: неупорядоченные элементы на "большом" конце массива занимают правильные положения за один проход, но неупорядоченные элементы в начале массива поднимаются на свои места очень медленно. Поэтому, вместо того чтобы постоянно просматривать массив в одном направлении, в последовательных проходах можно чередовать направления. Таким образом, элементы, сильно удаленные от своих положений, быстро станут на свои места. Данная версия пузырьковой сортировки носит название шейкер-сортировки (shaker sort сортировка перемешиванием, сортировка взбалтыванием, сортировка встряхиванием), поскольку действия, производимые ею с массивом, напоминают взбалтывание или встряхивание. Ниже показана реализация шейкер-сортировки.
//Описание функции шейкер-сортировки
void Shaker(int k,int x[max]){
int i,t;
bool exchange;
do {
exchange = false;
for(i=k-1; i > 0; --i) {
if(x[i-1] > x[i]) {
t = x[i-1];
x[i-1] = x[i];
x[i] = t;
exchange = true;
}
}
for(i=1; i < k; ++i) {
if(x[i-1] > x[i]) {
t = x[i-1];
x[i-1] = x[i];
x[i] = t;
exchange = true;
}
}
} while(exchange);
//сортировать до тех пор, пока не будет обменов
}Хотя шейкер-сортировка и является улучшенным вариантом по сравнению с пузырьковой сортировкой, она по-прежнему имеет время выполнения порядка N2. Это объясняется тем, что количество сравнений не изменилось, а количество обменов уменьшилось лишь на относительно небольшую величину.

